Геометрический смысл производной

Пусть – некоторая кривая, – точка на кривой .

Рисунок 4.1 – Касательная к кривой

Любая прямая, пересекающая не менее чем в двух точках называется секущей.

Касательной к кривой в точке называется предельное положение секущей , если точка стремится к , двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую (т.е. график функции ). Пусть в точке он имеет невертикальную касательную . Ее уравнение: (уравнение прямой, проходящей через точку и имеющую угловой коэффициент ).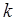

Рисунок 4.2 – Геометрический смысл производной

По определению углового коэффициента

,

где – угол наклона прямой к оси .

Пусть – угол наклона секущей к оси , где . Так как – касательная, то при

,

⇒ ,

⇒ .

Следовательно,

.

Таким образом, получили, что – угловой коэффициент касательной к графику функции в точке (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой в точке можно записать в виде

4.1.2 Понятие определенного интеграла. Геометрический и физический смысл определенного интеграла

В основе определения понятия определенный интеграл лежит понятие интегральная сумма. Пусть на отрезке [a, b] задана непрерывная функция f(x). Будем называть криволинейной трапецией фигуру ограниченную графиком функции, осью ОХ и вертикальными прямыми, проходящими через концы отрезка (Рис.4.3).

M

m

0 a=x₀ x_i-1 ζ x_i x_n= b x

Рисунок 4.3 – Смысл производной

Пусть функция определена на отрезке . Выполним следующие действия.

1. С помощью точек разобьём отрезок на n частичных отрезков .

2. В каждом частичном отрезке , i=1,2,…,n выберем произвольно точку и вычислим значение функции в ней, т.е. величину .

3. Умножим найденное значение функции на длину соответствующего частичного отрезка: .

4. Составим сумму S_n указанных произведений:

.

Сумма вида называется интегральной суммой функции на отрезке .

Обозначим через длину наибольшего частичного отрезка: .

5. Найдём предел интегральной суммы, при так, что .

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число I называется определённым интегралом от функции на отрезке и обозначается . Таким образом, .

Числа и называются соответственно нижним и верхним пределами интегрирования, – подынтегральной функцией, – подынтегральным выражением, – переменной интегрирования, отрезок - областью (отрезком) интегрирования.

Функция , для которой на отрезке существует определённый интеграл , называется интегрируемой на этом отрезке.

Основные свойства определённого интеграла

1. , где с – число

2.

Свойство 2 справедливо для любого конечного числа слагаемых.

3.

4. , где a<c<b

Свойство 4 позволяет разбивать отрезок интегрирования на части. Свойство 4 называют аддитивностью определённого интеграла. Свойство применяют при вычислении площадей фигур.

Определённый интеграл применяют для решения геометрических и физических задач. Например, вычисление площадей фигур, объёмов тел вращения, работы переменной силы, расстояния при прямолинейном перемещении, длины дуги плоской кривой, объёма тел, площади поверхности вращения, статических моментов и координат центра тяжести плоской кривой и многие другие прикладные задачи.

Вычисление определённого интеграла.

Для вычисления определённого интеграла от функции f(x) на отрезке применяют формулу Ньютона-Лейбница:

,

т.е. для вычисления определённого интеграла надо найти соответствующий неопределённый интеграл, а затем вычислить разность значений первообразной при верхнем и нижнем пределах интегрирования.

Формулу Ньютона-Лейбница также записывают в виде:

Пример. Вычислить .

Найдём одну из первообразных для функции

, т.е.

Тогда по формуле Ньютона-Лейбница

Решение записывают в виде:

Геометрический смысл определённого интеграла: определённый интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

Таблица 4.1 –Нахождение площади фигуры с помощью определенного интеграла

Q	№	Чертеж	Система координат и пояснения	Формула
S, площадь фигуры   п л о с к о й   ф и г у р ы   D			Декартова система координат Одна кривая границы области D не выше другой.
		Декартова система координат Одна кривая границы области D не левее другой.
		Декартова система координат a £ t £ b x (a) =a, x (b) =b (y(t) ³0, " tÎ [a,b ]) Верхняя граница области задана параметрически
	β α ρ2(φ) ρ1(φ)	Полярная система координат

Физический смысл определённого интеграла (работа переменной силы, путь при неравномерном движении точки, масса неоднородного стержня)

1. − сила, параллельная оси 0 Х и ориентированная в положительном направлении оси 0 Х, действующая на материальную точку при прямолинейном перемещении по промежутку [ a, b ]. Работа А силы при этом равна: .

2. − скорость неравномерного прямолинейного движения материальной точки.

Путь , пройденный точкой за промежуток времени ,

при этом равен: .

3. 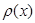− плотность неоднородного прямолинейного стержня с концами в точках .

Масса m такого стержня равна: .

4.1.3 Производная и определенный интеграл в программе SMath Studio

Для нахождения производной функции в программе SMath Studio используется функция diff(2) или diff(3). Отличие первой от второй заключается в том, что первая находит производную функции первого порядка, а вторая функция находит производную n -порядка. Также на панели инструментов «Функции» есть кнопка «Дифференцирование» для нахождения производной функции первого порядка (рис. 4.4).

Рисунок 4.4 – Кнопка «Дифференцирование» на панели инструментов «Функции»

Для решения определенного интеграла в программе SMath Studio используется функция «int». Также на панели инструментов «Функции» есть кнопка «Определенный интеграл» для решения определенных интегралов (рис. 4.5).

Рисунок 4.5 – Кнопка «Определенный интеграл» на панели инструментов «Функции»

Пример 1. Найдем производную функции первого и второго порядка (рис. 4.6-4.10).

На листе программы SMath Studio наберем функцию diff(2) (рис. 4.6)

Рисунок 4.6 – Вызов функции «diff(2)»

Получим шаблон (рис. 4.7).

Рисунок 4.7 – Шаблон функции «diff(2)»

В знаменатель шаблона внесем переменную z, а напротив черты дроби внесем нашу функцию.

Наберем функцию diff(3) (рис. 4.8)

Рисунок 4.8 – Вызов функции «diff(3)»

Получим шаблон (рис. 4.9).

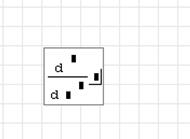
Рисунок 4.9 – Шаблон функции «diff(3)»

Конечный вид документа на рис. 4.10.

Рисунок 4.10 – Конечный вид документа нахождения производных

Пример 2. Найдем решение определенного интеграла

Для решения определенного интеграла на панели инструментов «Функции» нажмем кнопку «Определенный интеграл» и получим шаблон (рис. 4.11).

Рисунок 4.11 – Шаблон функции «int»

Заполним шаблон нашими данными и получим результат (см. рис. 4.12).

Рисунок 4.12 – Конечный вид документа нахождения решения определенного интеграла

Date: 2016-05-25; view: 617; Нарушение авторских прав