
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа №4. Дискретная свертка и фильтрация сигнала
Цель работы: Изучить один из методов фильтрации сигналов с использованием алгоритма секционированной свертки.
Необходимые теоретические сведения
Демонстрация возможностей ДПФ для фильтрации сигнала была рассмотрена в работе №1. В данной работе рассмотрена фильтрация с помощью цифрового фильтра (ЦФ) на основе секционированной свертки и ДПФ.
Выходной сигнал цифрового фильтра можно рассчитать, используя соответствующие структуре фильтра разностные уравнения. Достоинством такого неэффективного подхода является то, что он наглядно демонстрирует работу ЦФ и позволяет определить многие характеристики ЦФ. Реакцию (выходной сигнал) y [ n ] ЦФ на произвольное входное воздействие x [ n ] можно представить с помощью импульсной характеристики фильтра h [ n ], которая по определению является откликом фильтра на единичный импульс d[ n ]. Соотношение, связывающее вход и выход ЦФ носит название линейной свертки, соответствует работе нерекурсивного фильтра и имеет вид
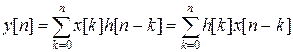 . .
| (1) |
Если последовательности x [ n ] и h [ n ] имеют длину, соответственно N 1 и N 2, то выходной сигнал будет иметь длину N = N 1+ N 2-1 и n = 0,1,2,…, N 1+ N 2-2. Предполагается, что x [ k ] = 0 и h [ k ] = 0 при k < 0.
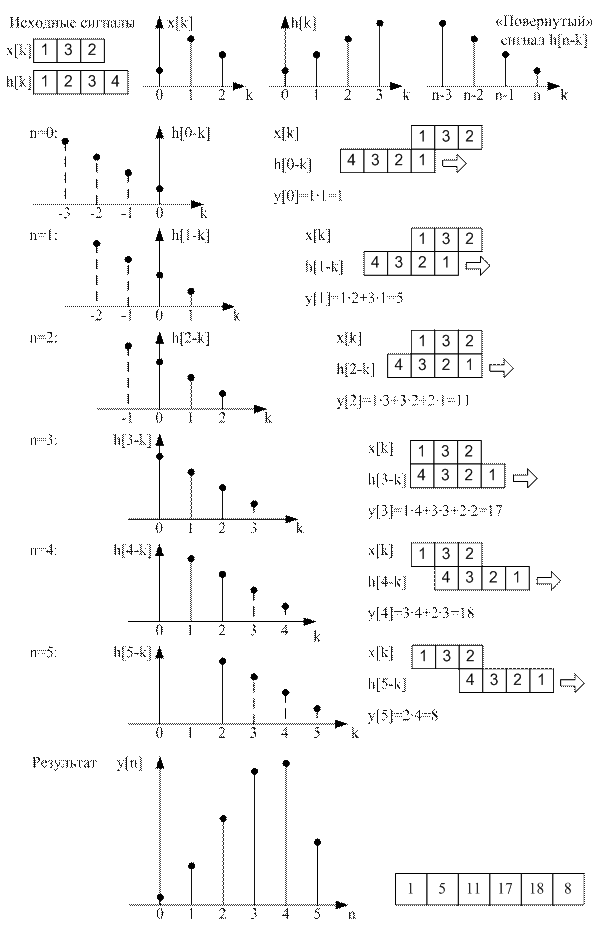
В соответствии с (1) выходной сигнал ЦФ определяется как сумма предыдущих входных воздействий, взвешенных на определенные значения импульсной характеристики при нулевых начальных условиях и произвольном входном сигнале. Обратим внимание, что импульсная характеристика поворачивается относительно оси ординат (зеркально отражается) и затем сдвигается вправо на n отсчетов, так что в результате получается зависимость h [ n - k ] (рис. 1).
|
| Рисунок 1 – Вычисление дискретной свертки |
Для вычисления линейной свертки при больших N 1 и N 2 может быть использован алгоритм вычисления круговой свертки
Для периодических последовательностей используется понятие круговой свертки, вычисляемой по выражениям
 , ,
| (2) |
где xN [ n ] и hN [ n ] - периодические последовательности с периодами по N отсчетов. Выходная последовательность yN [ n ] также будет периодической, поэтому достаточно ее вычислить на одном периоде.
Непосредственное вычисление по формулам (1) и (2) требует большого количества умножений: N 1∙ N 2 для линейной свертки и N 1(N 2+1) для круговой. Для круговой свертки количество умножений можно уменьшить с помощью БПФ. Этот же метод можно использовать с небольшими изменениями и для линейной свертки.
Для этого последовательности x [ n ] и h [ n ] дополняются нулевыми отсчетами, число которых равно (N - N 1) и (N - N 2) соответственно для x [ n ] и h [ n ] до N 1+ N 2-1 отсчета. Затем рассчитываются N - точечные ДПФ XN [ k ] и HN [ k ] и определяется их произведение YN [ k ]= XN [ k ] HN [ k ]. Наконец, с помощью обратного ДПФ для YN [ k ] рассчитывается круговая (периодическая) свертка yN [ n ], первые N = N 1+ N 2-1 отсчетов которой соответствуют искомой линейной свертке, т.е. выходному сигналу ЦФ. Дополнение исходных последовательностей конечной длины x [ n ] и h [ n ] нулевыми отсчетами доводит период yN [ n ] до нужной величины N = N 1+ N 2-1, что позволяет устранить наложения, характерные для круговой свертки.
Рассмотренный метод вычисления линейной свертки называется быстрой сверткой, поскольку использование алгоритмов БПФ позволяет существенно увеличить эффективность вычислений по сравнению с прямой сверткой, выполняемой в соответствии с (2).
На практике часто N 1>> N 2, причем величина N 1 может быть очень большой (или вообще неизвестной - например, при обработке сигналов в реальном времени), поэтому при вычислениях в соответствии с приведенным выше алгоритмом быстрой свертки возникают большие задержки или вычисления невозможно выполнить из-за ограниченных ресурсов памяти. В этом случае применяется алгоритм секционированной свертки. Исходный сигнал разбивают на короткие участки (секции) длиной M, как правило, соизмеримые с длиной импульсной характеристики и отвечающие условию M ≥ N 2, при котором перекрываются только две соседние i и (i +1)-я частичные свертки (рис.2). Результирующий сигнал y [ n ] ищется путем объединения результатов ДПФ на смежных участках длиной (N 2-1), где N 2 - длина импульсной характеристики.
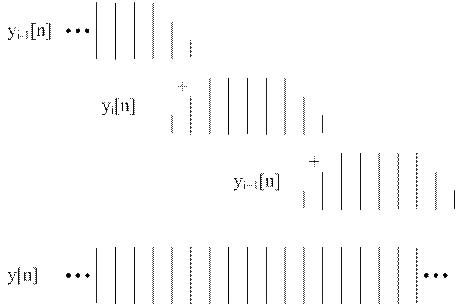
|
| Рисунок 2 – Перекрытие с суммированием |
Обработка предыдущей секции сигнала при этом совмещается с записью новой, так что запаздывание выходного сигнала во времени не превышает длины одной секции.
Данный алгоритм секционированной свертки называется перекрытием с суммированием (overlap-add). Другой возможный вариант – перекрытие с накоплением (overlap-save). Входной сигнал разбивается на блоки, которые перекрываются по краям на (N 2-1) отсчет. У получаемого выходного сигнала для каждого блока откидываются крайние участки длиной по (N 2-1) отсчетов с каждого края. Потом секции объединяются без перекрытия. Результирующая последовательность будет иметь длину N = N 1+ N 2-1.
Практическая часть
Алгоритм секционированной свертки с суммированием
1. Пусть есть сигнал x [ n ], n =0,..., N -1, N - такое большое, что сигнал не может поместиться в память, а может и бесконечное.
2. Есть импульсная характеристика фильтра h [ n ], n =0,..., N 2.
3. Разобьем сигнал x [ n ] на выборки по N 1 отсчетов в каждой, N 1 << N и N 1> N 2 (будем считывать из x [ n ] выборки по N 1 значений).
4. Определим L ³ N 1+ N 2-1, такое, что L =2 p. Т.е. L ближайшее сверху (N 1+ N 2-1) число степени 2.
5. Выберем из x [ n ] последовательность x 1[ n ] длины N 1 (первая выборка п.3).
6. Расширим последовательности x 1[ n ] и h [ n ] до L значений, дополнив их нулями: x 1[ n ]=0, при n = N 1,... L -1, h [ n ]=0, при n = N 2,..., L -1.
7. Используя процедуру БПФ, вычислим преобразование Фурье X 1[ k ], H [ k ], k =0,..., L -1
8. Получим Y 1[ k ]= X 1[ k ]× H [ k ], k =0,.., L -1.
9. С помощью обратного преобразования Фурье получим сигнал y 1[ n ], n =0,..., L -1. y 1[ n ] - обратное БПФ от Y 1[ k ].
10. Только первые N 1+ N 2-1 отсчета последовательности y 1[ n ] будут отличны от нуля. Но правильными будут только первые N 1 отсчетов, которые мы и запоминаем в выходной последовательности y [ n ].
11. Оставшиеся N 2 (N 2-1, но для простоты захватим еще один нулевой отсчет) отсчета запоминаем во временном массиве t [ n ]: t [ n ]= y 1[ N 1+ n ], n =0,..., N 2 - 1.
12. Вернемся к пункту 5, но со следующей выборкой из массива x [ n ], т.е. следующие N 1 отсчета. Когда дойдем до пункта 10, выполним следующее. Первые N 2 отсчета результирующего y 1[ n ] сложим с t [ n ] и все N 1 отсчетов y 1[ n ] сохраним как результат: y [ n ]= y 1[ n ]+ t [ n ], n =0,..., N 2-1; y [ n ]= y 1[ n ], n = N 2,..., N 1-1. И запомним в t [ n ] оставшиеся ненулевые отсчеты y 1[ n ]: t [ n ]= y 1[ N 1+ n ], n =0,..., N 2-1.
13. Далее алгоритм продолжается, пока не будет отфильтрован весь сигнал.
Графически описанный выше алгоритм показан на рис. 3. Для наглядности использованы промежуточные массивы x 1[ n ], h 1[ n ], y 1[ n ], отличающие по длине от исходных x [ n ], h [ n ], y [ n ].
Т.к. на рис.3 первый этап выполняется иначе, чем второй и последующие, то на рис. 4 показан более удобный вариант для программной реализации.

|
| Рисунок 3 – Алгоритм секционированной свертки |

|
| Рисунок 4 – Алгоритм секционированной свертки для программирования |
Счетчик циклов-этапов k изменяется от 0 до некоторого значения, которое указывает, сколько раз блок считываемых данных N 1 укладывается в N с округлением в большую сторону. Если же N бесконечно (или заранее неизвестно), то k увеличивается, пока на вход поступают данные.
Описание использования программного модуля
На рис. 5 показанное исходное состояние программы после запуска.

|
| Рисунок 5 – Главное окно программного модуля |
На форме есть две кнопки «Открыть»: одна для входного сигнала, который необходимое отфильтровать, другая – для импульсной характеристики фильтра. Когда данные загрузятся, в поле «N=» будет показана длина сигнала, а в поле «N2=» длина импульсной характеристики.
После загрузки соответствующих файлов становится доступной поле ввода «Длина секции N1» и кнопка «Подготовить». Кнопку «Подготовить» необходимо использовать каждый раз после загрузки другого сигнала или импульсной характеристики, а также при изменении длины секции. В поле «Длина секции N1» необходимо ввести величину, большую чем в поле «N2=» (согласно алгоритму). Если данные корректные, то после нажатия кнопки «Подготовить» в поле «L=» появится значения длины секции для расчетов с помощью БПФ, а в поле «Раундов» - количество раундов расчетов (число секций).
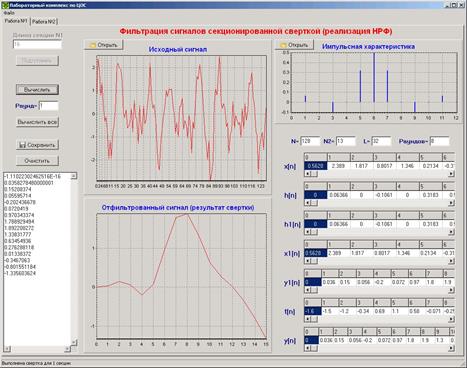
После этого можно нажимать кнопку «Вычислить» или «Вычислить все». При нажатии первой из них будет выполнен расчет одного раунда, в поле «Раунд» отобразится цифра «1», а на графической панели «Отфильтрованный сигнал (результат свертки)» будет выведен результат расчетов (рис. 6).
|
| Рисунок 6 – Результат выполнения первого раунда фильтрации |
Кроме того, в числовом поле слева внизу окна программы будут показаны числовые значения расчетов, которые можно просмотреть с помощью полосы прокрутки или сохранить в файл. При повторном нажатии кнопки «Вычислить» будет рассчитан второй раунд (рис 7). При этом программа разработана так, чтобы количество раундов не превысило расчетное, после чего кнопки «Вычислить» и «Вычислить все» будут заблокированы. Кнопку «Вычислить все» можно нажать или с самого начала или в любой момент выполнения работы после нажатия кнопки «Вычислить». При этом сразу будет получен конечный результат, который выводится на график и который можно сохранить в файл при нажатии кнопки «Сохранить» (рис. 8).
Содержимое всех массивов данных можно просматривать во время счета с помощью таблиц, которые располагаются по правую сторону, под графической панелью «Импульсная характеристика» (рис. 6-8).

|
| Рисунок 7 – Результат выполнения второго раунда фильтрации |

|
| Рисунок 8 – Результат выполнения всех раундов фильтрации сигнала |
Порядок выполнения работы
Данная работа выполняется на ПЭВМ с использованием программы «Лабораторный комплекс по ЦОС» и MathCAD 15. До занятия выполняются пп. 1 и 2. На занятии – пп., начиная с 3.
1. Изучить работу с программным модулем «Фильтрация сигнала секционированной сверткой (реализация НРФ)» (далее для сокращения просто «Секционированная свертка»).
2. Разработать и нарисовать блок-схему алгоритма для программной реализации на MathCAD.
3. Запустить программный модуль «Секционированная свертка».
4. Считать с диска отсчеты измеренного сигнала и импульсную характеристику. Номер задания узнать у преподавателя.
5. Выполнить фильтрацию сигнала с помощью модуля «Секционированная свертка» и сохранить результат в файл на диск. На этом экспериментальная часть лабораторной работы заканчивается.
6. Запустить MathCAD.
7. Считать с диска отсчеты измеренного сигнала и импульсную характеристику. Построить графики введенных значений.
8. Используя приведенный на рис. 4 алгоритм и его текстовое описание, самостоятельно разработать в MathCAD программную реализацию.
9. Отфильтровать сигнал и построить в MathCAD выходной сигнал разработанного фильтра.
10. Ввести в MathCAD значения отфильтрованного сигнала, полученные в п.4 задания и сравнить с полученным результатом п.7. При правильной реализации п 7. результаты должны совпасть.
Оформление отчета
В отчете необходимо представить графики исходного и отфильтрованного сигналов, программу, написанную в MathCAD с пояснением всех операций и результаты сравнения работы программы MathCAD с результатом программного модуля «Секционированная свертка».
Вопросы к лабораторной работе
1. Каким методом в данной работе рассчитывается выходной сигнал ЦФ?
2. В чем достоинством метода расчета выходного сигнала ЦФ, который используется в данной работе?
3. С помощью какого выражения можно найти реакцию (выходной сигнал) ЦФ на произвольное входное воздействие? Как называется это соотношение?
4. Что такое импульсная характеристика фильтра? Как она обозначается?
5. Как выглядит выражение для выполнения z-преобразования импульсной характеристики?
6. Что такое круговая свертка? Когда она используется?
7. Как выглядит выражение для вычисления круговой свертки?
8. В каких случаях применяется алгоритм секционированной свертки? В чем его смысл?
9. Каким образом увеличивают скорость проведения вычислений при использовании секционированной свертки?
10. Почему выполнение первого этапа алгоритма по рис. 3 отличается от всех последующих этапов?
11. За счет чего удалось добиться унификации выполнения всех этапов алгоритма по рис. 4?
12. Что является счетчиком цикла (этапов)? Когда наступает конец выполнения программы?
Лабораторная работа №5. Синтез нерекурсивных цифровых фильтров (методом окон)
Цель работы: Изучить синтез нерекурсивных фильтров методом взвешивания.
Теоретическая часть
Цифровой фильтр в узком смысле – это частотно-избирательная цепь, которая обеспечивает пропускание сигналов в определенных полосах частот и подавление в других. Область частот, в которой фильтр пропускает сигнал, называют полосой пропускания, а область частот, в которой ослабление входного сигнала велико - полосой задерживания. В зависимости от взаимного расположения полосы пропускания и полосы задерживания различают: фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), полосовой фильтр (ПФ), заграждающий (режекторный) фильтр (ЗФ). Идеальные АЧХ указанных фильтров изображены на рис. 1.

|
| Рисунок 1 – Идеальные АЧХ фильтров: а) фильтр нижних частот; б) фильтр верхних частот; в) полосовой фильтр; г) режекторный фильтр. |
По виду передаточной функции и соответственно, структуре, ЦФ делятся на две группы: нерекурсивные и рекурсивные.
Фильтры со структурой на рис. 2 носят название нерекурсивные (НРФ) (другой термин – трансверсальные) цифровые фильтры. Их работа подчиняется разностному уравнению  , а передаточная функция равна
, а передаточная функция равна  .
.

|
| Рисунок 2 – Структурная схема нерекурсивного (трансверсального) цифрового фильтра. |
Поскольку количество элементов задержки в реальном трансверсальном фильтре конечно, конечным является и количество ненулевых отсчетов импульсной характеристики фильтра, то есть импульсная характеристика такого фильтра конечна. Фильтры, обладающие таким свойством, принято выделять в отдельный класс и называть КИХ-фильтрами.
Основные достоинства КИХ-фильтров [2]:
1. КИХ-фильтры легко создавать со строго линейной фазовой характеристикой arg H (e j ω).
2. КИХ-фильтры можно эффективно строить как по рекурсивным так и по нерекурсивным схемам.
3. КИХ-фильтры, реализуемые нерекурсивно, т.е. с помощью прямой свертки, всегда устойчивы.
4. При нерекурсивной реализации КИХ-фильтров шумы округления, возникающие за счет выполнения арифметических операций с конечной точностью, легко минимизировать.
5. Может быть адаптивным.
6. Легкое понимание принципов работы и проектирования.
Недостатки КИХ-фильтров [2]:
1. Для аппроксимации фильтров, частотные характеристики которых имеют острые срезы, требуется импульсная характеристика с большим числом отсчетов N. Поэтому при обычной свертке необходимо выполнять большой объем вычислений.
2. Задержка в КИХ-фильтрах с линейной фазовой характеристикой не всегда равна целому числу интервалов дискретизации. В некоторых приложениях такая некратная задержка может вызвать определенные трудности.
Реальные цифровые фильтры, обрабатывающие временные дискретные сигналы, должны отвечать принципу причинности, согласно которому сигнал на выходе не может появиться до прихода первого ненулевого отсчета входного сигнала. Такие фильтры называются физически реализуемыми или каузальными фильтрами, их импульсная характеристика должна подчиняться требованию:
| h [ n ] = 0 при n < 0. | (1) |
Задание требований к цифровым фильтрам
Частотно-избирательные фильтры обычно синтезируются в частотной области. При этом в процессе синтеза сами частоты могут задаваться как действительными f [Гц], ω [рад/с], так и нормированными w [рад] или W значениями. С учетом периодичности требования к частотным характеристикам фильтров обычно задают на интервале частот [0, π/ T 0] (или [0, ωд/2]). При этом для сопоставления фильтров используют нормирование. Существует два способа нормирования. В первом случае нормированная частота w вводится путем умножения частоты ω на период дискретизации T 0:
| w = ω· T 0; при ωд = 2π/ T 0, w д = 2π (или w = 2π· f · T 0 = 2π· f ·/ f д; при f д = 1/ T 0, w д = 2π) | (2а) |
и требования к фильтрам задают на интервале [0, π].
Во втором случае используют нормировку по частоте делением на частоту дискретизации ωд:
| Ω= ω/ωд; при ω=ωд нормированное значение Ωд = 1. | (2б) |
В этом случае требования к фильтрам задают па интервале [0; 0,5].
В частотной области требования могут предъявляться:
1. Только к амплитудно-частотной характеристике (АЧХ) без каких-либо ограничений на фазочастотную характеристику (ФЧХ).
2. Только к ФЧХ, когда важно сохранение фазовых, а потому и временных соотношений между гармоническими составляющими принимаемого сигнала.
3. Одновременно и к АЧХ, и к ФЧХ.
Требования к частотно-избирательным фильтрам включают в себя:
1. Задание частоты дискретизации ωд и типа избирательности (НЧ, ВЧ и т.д.).
2. Задание требований к АЧХ H (e j ω) – форме, неравномерности.
3. Выбор метода аппроксимации АЧХ (может выбираться разработчиком).
При синтезе ЦФ вместо частот среза ωС, ωСН, ωСВ (рис. 1) могут задаваться частоты ωЗ и ωП, ωЗН и ωПН, ωЗВ и ωПВ, соответственно (рис. 4). В этом случае, при синтезе КИХ-фильтров методом окон, частоты ωС, ωСН, ωСВ могут быть найдены с использованием следующих формул:
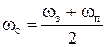 , ,  , , 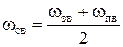 . .
| (3) |
Значение величины АЧХ, на частотах среза ωС, ωСН, ωСВ, у фильтров, синтезированных с использованием метода окон, составляет в логарифмическом масштабе -6 дБ.
Диаграммы требований к АЧХ фильтров показаны на рис. 4.

|
| Рисунок 4 – Диаграммы требований к АЧХ фильтров: а) фильтр нижних частот; б) фильтр верхних частот; в) полосовой фильтр; г) режекторный фильтр. |
Фильтр нижних частот (low- pass filter)
Реальный ФНЧ имеет три частотные полосы (рис. 4а): полосу пропускания (ПП), переходную полосу, и полосу задерживания (ПЗ) или иначе ослабления.
Коэффициент передачи в полосе пропускания H 1, обычно равен 1.
Полоса пропускания ограничивается граничной частотой в ПП ωП; ширина ПП DωПП = ωП; dП – максимальное отклонение АЧХ от желаемой (в единицах коэффициента передачи) в ПП, часто выражаемое в дБ с использованием величины R, получившей название максимально допустимого затухания в ПП (неравномерность в ПП):
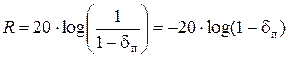 . .
| (4) |
Переходная полоса располагается между полосами пропускания и задерживания; ширина переходной полосы Dω = ωЗ.- ωП. Поскольку в этой полосе требования не задаются, удовлетворительным окажется любое решение, если оно соответствует требованиям в полосах пропускания и задерживания.
Полоса задерживания (ослабления) лежит в пределах от граничной частоты в ПЗ ωЗ до половины частоты дискретизации ωД/2; ширина ПЗ DωПЗ = ωД/2 - ωЗ; dЗ – отклонение АЧХ от 0 в ПЗ, часто выражаемое в дБ с использованием величины A, получившей название минимально допустимого затухания в ПЗ (затухание в ПЗ):
 . .
| (5) |
Фильтр верхних частот (high-pass filter)
Реальный ФВЧ имеет, как и ФНЧ, три частотных полосы, которые расположены в обратном, относительно ФНЧ, порядке (рис. 4б).
Полоса задерживания лежит в пределах от 0 до ωЗ; ширина ПЗ DωПЗ = ωЗ.
Переходная полоса лежит в пределах от ωЗ до ωП; ширина переходной полосы Dω = ωП - ωЗ.
Полоса пропускания лежит в пределах от ωП до ωД/2; ширина ПП DωПП = ωД/2 - ωП.
Полосовой фильтр (band-pass filter)
Реальный ПФ характеризуется пятью частотными полосами (рис. 4в), из которых одна – центральная – полоса пропускания, две полосы задерживания и две переходные полосы. Обозначения, приведенные на рис. 4в, следующие:
ωЗН – граничная частота первой полосы задерживания (ПЗ1); ширина ПЗ1 DωПЗ1 = ωЗН;
ωПН – нижняя граничная частота ПП; ωПВ – верхняя граничная частота ПП; ширина ПП DωПП = ωПВ - ωПН;
ωЗВ – граничная частота второй полосы задерживания (ПЗ2); ширина ПЗ2 DωПЗ2 = ωД/2 - ωЗВ.
Переходные полосы 1 и 2 имеют ширину Dω1 = ωПН - ωЗН и Dω2 = ωЗВ - ωПВ.
Заграждающий (режекторный) фильтр (band-stop filter)
Реальный ЗФ (иногда называют полосно-заграждающим), подобно ПФ характеризуется пятью полосами (рис. 4г), из которых две полосы пропускания, одна полоса задерживания и две переходные полосы. Обозначения, приведенные на рис. 4г, следующие: ωПН – граничная частота первой полосы пропускания (ПП1); ширина ПП1 DωПП1 = ωПН;
ωЗН – нижняя граничная частота ПЗ; ωЗВ – верхняя граничная частота ПЗ; ширина ПЗ DωПЗ = ωЗВ - ωЗН;
ωПВ – граничная частота второй полосы пропускания (ПП2); ширина ПП2 DωПП2 = ωД/2 - ωПВ.
Переходные полосы 1 и 2 имеют ширину Dω1=ωЗН - ωПН и Dω2=ωПВ - ωЗВ.
Синтез нерекурсивных КИХ-фильтров
Если исходными данными для проектирования является именно импульсная характеристика фильтра, то проектирование не требует вообще никаких усилий. Обычно, однако, исходными данными является требуемая амплитудно-частотная характеристика фильтра (АЧХ) H (ω).
Синтез НРФ состоит в определении импульсной характеристики фильтра h [ k ], обеспечивающей выполнение требований, предъявляемых к фильтру. Обычно эти требования задаются в виде желаемых частотных характеристик. Импульсная характеристика h [ k ] НРФ является конечной и определяется для значений k, лежащих в диапазоне [0, N -1]. Синтез НРФ предусматривает выполнение следующих основных этапов:
1) определение числа коэффициентов фильтра N (порядка фильтра);
2) выбор метода синтеза (метода аппроксимации), минимизирующего отклонение между желаемыми и реальными характеристиками фильтров;
3) вычисление коэффициентов НРФ в соответствии с выбранным методом. Напомним, что для НРФ коэффициенты фильтра b [ k ] равны отсчетам импульсной характеристики h [ k ];
4) анализ результатов синтеза и принятие решений относительно свойств синтезированного фильтра.
Если результаты синтеза не удовлетворяют заданным требованиям, то выполняют повторный синтез при других значениях N или выбирают другой метод синтеза.
Импульсная характеристика КИХ-фильтров с линейной фазой
Поскольку частотная характеристика любого идеального цифрового фильтра H (e j ω) является периодической функцией частоты с периодом T 0 частоты дискретизации ωд, то она связана с импульсной характеристикой h [ n ] парой дискретно-непрерывных преобразований Фурье (ДНПФ):
 , ,

| (6) |
Тогда, нормируя частоту по (2а), выражения (6) можно переписать (с учетом T 0· d ω = dT 0ω = dw и изменения пределов интегрирования на интервал от -π до +π)
 , ,
| (7) |
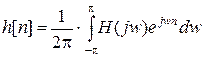 . .
| (8) |
Ясно, что это – физически нереализуемый БИХ-фильтр, поскольку импульсная характеристика бесконечна и при n < 0 h [ n ] ≠ 0 – то есть реакция фильтра опережает воздействию. Поэтому в таком виде она не может быть непосредственно использована в качестве импульсной характеристики НРФ.
Получить на основе импульсной характеристики (8) физически реализуемый КИХ-фильтр с частотной характеристикой, близкой к заданной, можно двумя операциями. При первой – ограничении ряда (4) до N членов (от – K до K, K =(N – 1)/2, для упрощения полагаем N – нечетное), получаем характеристику КИХ – фильтра. При этом частотная характеристика фильтра аппроксимируется усеченным рядом Фурье (сравните с формулой (7)):
 . .
| (10) |
При второй – сдвиге h [ n ] вправо на K отсчетов, получаем физически реализуемый КИХ – фильтр. Для примера на рис. 5 показан результат операции усечения-сдвига импульсной характеристики ФНЧ с желаемой АЧХ, соответствующей рис. 1а.

|
| Рисунок 5 – Результат операции усечения-сдвига импульсной характеристики фильтра с желаемой АЧХ |
Будем рассматривать импульсные характеристики только с действительными отсчетами. Это значит, что АЧХ H (ω) является четной функцией частоты, а ФЧХ j(w) – нечетной: H (ω) = H (–ω), j(– w) = –j(w).
На практике при расчете КИХ-фильтров часто требуется строго линейная фазовая характеристика.
Рассмотрим, при каких условиях импульсная характеристика фильтра h [ n ] будет обеспечивать строгую линейность его фазовой характеристики. Требование линейности фазы фильтра означает, что фазовая характеристика j(w) должна иметь вид
| j(w) = α · w, –π < w < π, | (11) |
где α – постоянная фазовая задержка, выраженная через число интервалов дискретизации.
В [2] доказывается, что
| α = (N – 1)/2, | (12) |
и
| h [ n ] = h [ N -1 - n ], 0 ≤ n ≤ N – 1. | (13) |
Из условия (12) следует, что для каждого порядка фильтра N существует только одна фазовая задержка α, при которой может достигаться строгая линейность ФЧХ. Из условия (13) следует, что импульсная характеристика фильтра должна быть симметричной.
Возможны 2 варианта: N – нечетное и N – четное.
Если N – нечетное, то α – целое, т. е. задержка в фильтре равна целому числу интервалов дискретизации, а центр симметрии приходится на (N – 1)/2 отсчет. Если N – четное, то α – дробное, т. е. задержка в фильтре равна дробному числу интервалов дискретизации, а центр симметрии находится посередине между (N – 2)/2 и (N)/2 отсчетами.

|
| Рисунок 6 – Типичная импульсная характеристика при четном N (а) и при нечетном N (б) (четная симметрия) |
Если ФЧХ линейна, постоянна не только фазовая задержка α = j(w)/ w, но и групповая задержка t = – d j(w)/d w = const, т.е. при изменении частоты сигнала она не меняется и сигнал, проходящий через фильтр, не искажает своей формы. При нелинейной ФЧХ разные частоты приобретают разные фазовые сдвиги и соответственно разные временные задержки на выходе фильтра, приводящие к изменению формы сигнала.
Если достаточно, чтобы только групповая задержка была постоянной, можно определить еще один тип фильтра с линейной фазой, фазовая характеристика которого является кусочно-линейной функцией частоты w, т. е.
H (e jw) = ±| H (e jw)|·e j (β-α w).
В [2] показано, что в этом случае
| α = (N – 1)/2, | (14) |
| β = ±π/2, | (15) |
и
| h [ n ] = - h [ N -1 - n ], 0 ≤ n ≤ N – 1. | (16) |
Фильтры, удовлетворяющие условиям 14-16, снова создают задержку в (N -1)/2 интервалов дискретизации, но их импульсные характеристики в отличие от предыдущего случая антисимметричны относительно центра. Как и в предыдущем случае, возможны 2 варианта импульсных характеристик: для фильтров с нечетным и четным N. Следует отметить, что для нечетных значений N, согласно (16), h [(N - 1)/2] = 0. Условия 14 – 16 используются при расчете широкополосных дифференциаторов и преобразователей Гильберта.
Итак, в зависимости от значения N (нечетные или четные) и вида симметрии импульсной характеристики (симметричная или антисимметричная характеристика) возможны четыре различных вида КИХ-фильтров с линейными фазовыми характеристиками:
1) N - нечетное и коэффициенты симметричны h [ n ] = h [ N – 1 - n ];
2) N - четное и коэффициенты симметричны h [ n ] = h [ N – 1 - n ];
3) N - нечетное и коэффициенты антисимметричны h [ n ] = - h [ N – 1 - n ];
4) N - четное и коэффициенты антисимметричны h [ n ] = - h [ N – 1 - n ].
Частотная характеристика КИХ-фильтров с линейной фазой
Выразим функцию H (e j ω) через значения коэффициентов импульсной характеристики. Рассмотрим сначала некаузальный НРФ с симметричной импульсной характеристикой
| h НК[- n ]= h НК[ n ], n = 1,2,…, K, K =(N -1)/2, N – нечетное. | (17) |
Частотная характеристика такого фильтра (10) запишется в виде
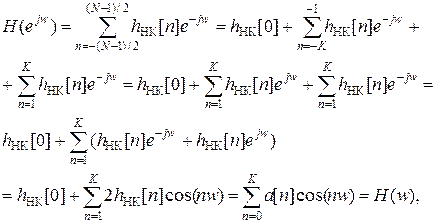
| (18) |
где a [ n ] = 2 h НК[ n ] кроме a [0] = h НК[0]. Таким образом, частотная характеристика некаузального НРФ является действительной функцией и характеризуется нулевым сдвигом фазы.
Импульсная характеристика каузального НРФ первого вида может быть получена из (18) путем задержки на K =(N -1)/2 тактов. В частотной области эта задержка соответствует сдвигу фазы, определяемому множителем 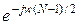 . Поэтому частотная характеристика НРФ первого вида запишется в виде
. Поэтому частотная характеристика НРФ первого вида запишется в виде
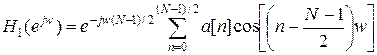 , ,
| (19) |
где a [ n ] = 2 h НК[ n - K ], кроме a [ K ] = h НК[ n - K ].
Множитель 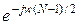 обеспечивает линейную зависимость фазы от частоты, отбрасывая его, получим модуль комплексной частотной характеристики | H (e j ω)|, т.е. АЧХ H (w).
обеспечивает линейную зависимость фазы от частоты, отбрасывая его, получим модуль комплексной частотной характеристики | H (e j ω)|, т.е. АЧХ H (w).
Для фильтров второго вида с симметричной h [ n ] и четным N в выражение для частотной характеристики необходимо дополнительно внести задержку на половину такта и вместо функций cos(nw) использовать функции cos(n +0,5) w [2]:
 , ,
| (20) |
где b [ n ] = 2 h НК[ n - K ].

| (21) |
Необходимо отметить, что H 2(w) = 0 при w = π и независимо от значений h [ n ]. Отсюда следует, что нельзя использовать фильтры этого вида для аппроксимации частотной характеристики, отличной от нуля при w = π (например, при проектировании фильтров верхних частот или режекторных фильтров).
Для фильтров третьего вида с антисимметричной h [ n ] и нечетным N выражение, определяющее частотную характеристику, почти аналогично (16), но вместо cos(nw) необходимо подставить sin(nw) и учесть дополнительный сдвиг на π/2 согласно (15) [2]:
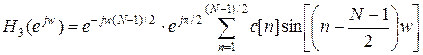 , ,
| (22) |
где c [ n ] = 2 h НК[ n - K ] и c [0] = h НК[ K ] = 0.

| (23) |
Видно, что H 3(w)=0 на частотах w = 0 и w = π; независимо от значений h [ n ]. Более того, множитель e j π/2 = j в формуле (20) показывает, что без учета множителя с линейным изменением фазы частотная характеристика является чисто мнимой функцией. Поэтому этот вид фильтров наиболее пригоден для проектирования преобразователей Гильберта и дифференциаторов.
Для фильтров четвертого вида с антисимметричной h [ n ] и четным N выражение для частотной характеристики аналогично для фильтров второго типа с заменой косинусов на синус [2]
 , ,
| (24) |
где d [ n ] = 2 h НК[ n - K ].
 , ,
| (25) |
причем H 4(w)=0 на частотах w = 0. Следовательно, этот вид фильтров наиболее пригоден для проектирования преобразователей Гильберта и дифференциаторов.
Методы расчета КИХ-фильтров с линейными фазами
Известны три класса методов проектирования КИХ-фильтров с линейной фазой: методы взвешивания с помощью окна, методы частотной выборки и проектирование оптимальных (по Чебышеву) фильтров с минимаксной ошибкой. Все они имеет свои достоинства и недостатки, выбор метода проектирования определяется большим числом факторов и в каждом конкретном случае выбирается индивидуально.
Метод взвешивания (метод окон)
Основное достоинство метода взвешивания заключается в его простоте и легкости использования, во многом базирующиеся на том, что почти всегда можно найти замкнутые выражения для вычисления коэффициентов фильтра с использованием формул дискретно-непрерывного преобразования Фурье (6).
Когда же характеристика H (e j ω) имеет сложный вид или не может быть просто преобразована в замкнутое математическое выражение (а иногда и в случае, когда это возможно), формула (6) зачастую оказывается громоздкой или неудобной для интегрирования. В этом случае использование метода окон проблематично. Однако замена интегрирования в (6) на суммирование с большим числом членов [2] уменьшает значение этого недостатка.
Другой недостаток метода взвешивания заключается в отсутствии достаточной гибкости при выполнении проектирования. Например, при расчете фильтра нижних частот трудно, как правило, точно определить граничную частоту полосы пропускания, поскольку окно «размывает» разрыв идеальной характеристики. Результирующая характеристика имеет две граничные частоты - ωП для полосы пропускания и ωЗ для полосы задерживания. И хотя при разработке фильтров типа идеального фильтра нижних частот эффекты размытия удается скомпенсировать, для фильтров с более сложными характеристиками этого достичь непросто [2]. Т.е. метод взвешивания не является оптимальным в том смысле, что он не позволяет получить минимально возможные пульсации для заданного порядка фильтра N и заданного множества частот среза.
Еще одной особенностью, которая может препятствовать использованию метода взвешивания, является то, что для частотно-избирательных фильтров одинаково аппроксимируются переходные полосы и пульсации в полосе пропускания и полосе задерживания.
Рассмотренная ранее операция усечения (рис. 3) и (10) с точки зрения импульсной характеристики h [ n ] представляет собой умножение ее на последовательность v [ n ] (на прямоугольное весовое окно) длиной N отсчетов вида:
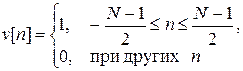
| (26) |
или
 , ,
| (27) |
в зависимости от того, усекаем мы вначале импульсную характеристику или сдвигаем (далее будем рассматривать смещенные окна при 0 ≤ n ≤ N – 1 (рис. 7)), т.е.
| h [ n ]= h З[ n - K ] v [ n ]. | (28) |
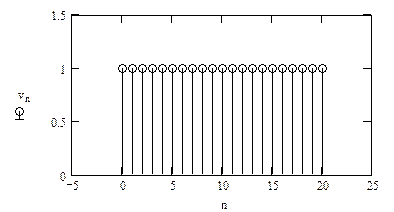
|
| Рисунок 7 – Прямоугольное окно при N =21, K =10 |
Синтезированный таким образом НРФ будет иметь значительные пульсации АЧХ в районе частоты среза (рис.8). Это явление получило название «эффект Гиббса». Размах пульсаций вблизи точки разрыва максимален слева и справа, составляет 9% от АЧХ и остается таким вне зависимости от N.

|
| Рисунок 8 – АЧХ ФНЧ при N =21, К =10 |
Частотная характеристика, соответствующая умножению заданной импульсной характеристики на прямоугольное окно (28), будет равна свертке заданной частотной характеристики с частотной характеристикой прямоугольного окна
 , ,
| (29) |
где * - символ свертки; θ - переменная интегрирования; 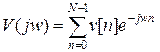 - частотная характеристика весовой функции, в данном случае прямоугольного:
- частотная характеристика весовой функции, в данном случае прямоугольного:
 , ,
| (30а) |
Функция (30) известна под названием ядра Дирихле. Если не учитывать множитель  , характеризующий линейный фазовый сдвиг, то график функции
, характеризующий линейный фазовый сдвиг, то график функции

| (30б) |
будет иметь форму, показанную на рис. 9, а ее модуль в области положительных частот - на рис. 10.

|
| Рисунок 9 – АЧХ прямоугольного окна при N =21 |
Это быстроколеблющаяся функция с максимальным значением N при w = 0, резко спадающая по амплитуде. Область с максимальной амплитудой называется главным лепестком, а остальные области - боковыми лепестками.

|
| Рисунок 10 – Модуль АЧХ прямоугольного окна при N =21 и w ³0 |
Функция V (jw) принимает нулевые значения на частотах w =2π k / N, k =1,2,…, N -1, а ширина всех лепестков, включая главный, одинакова и равна
| ΔωГЛ =2π/ N, | (31) |
причем с увеличением N ширина главного лепестка уменьшается и увеличивается число пульсаций. Иногда ширина главного лепестка выбирается вдвое больше той, которая определяется с использованием выражения (31). Последнее связано с тем, что главный лепесток модуля частотной характеристики окна математически определен как в положительной, так и в отрицательной области частот.
Таким образом, эффект Гиббса связан с пульсирующим поведением частотной характеристики прямоугольного весового окна.
Для уменьшения отрицательного влияния эффекта Гиббса применяют весовые окна, отличные от прямоугольного. С целью обеспечения линейности ФЧХ указанные оконные функции должны быть симметричными

| (32) |
Метод синтеза передаточной функции с помощью ограничения ряда (6) окном (32) называется методом окон или взвешивания. За счет выбора формы окна и его длины можно осуществить некоторое управление процессом расчета. Форма окна является существенной при определении минимального ослабления в полосе задерживания.
Можно сформулировать следующие требования к весовой функции окна, которая должна иметь:
- минимальную ширину главного лепестка ΔωГЛ:
- минимальный уровень боковых лепестков dБЛmax и минимальную площадь под боковыми лепестками;
- минимальную длину N.
Требования эти достаточно противоречивы. Так, более гладкие весовые функции имеют меньший уровень боковых лепестков, но большую ширину главного лепестка, уменьшающуюся с увеличением длины весовой функции N. Этим объясняется многообразие используемых на практике типов весовых функций, применение которых определяется характером поставленной задачи синтеза фильтров. Кроме прямоугольного окна чаще всего рассматривают обобщенное окно Хэмминга и окно Кайзера.
Параметры и математические описания некоторых из оконных функций приведены в Приложении.
Выбор окна [4]
Стратегия выбора окна диктуется компромиссом между смещением из-за помех в области близких боковых лепестков и смещением из-за помех в области дальних боковых лепестков. Например, если достаточно сильные компоненты помехи расположены вблизи и на отдалении от слабой компоненты сигнала, то следует выбирать окно с одинаковым уровнем боковых лепестков около главного лепестка, с тем чтобы обеспечить малое смещение; см. рис. 11, а.

| ||
| а | б | в |
| Рисунок 11 – Стратегия выбора окна: а - окно со слабо изменяющимся уровнем боковых лепестков при наличии близкой и удаленной помех сравнимого уровня; б - окно с быстро спадающим уровнем боковых лепестков при наличии сильной удаленной помехи; в - нетрадиционное окно специальной формы с малыми ближними и возрастающими дальними боковыми лепестками при наличии очень близкой помехи. |
Если же имеется одна сильная компонента помехи, удаленная от слабой компоненты сигнала, как доказано на рис. 11, б, то следует выбирать окно с быстро спадающим уровнем боковых лепестков, причем их уровень в непосредственной близости к главному лепестку в данном случае не имеет большого значения. В том случае, когда необходимо обеспечить высокое разрешение между очень близкими компонентами сигнала и помехи, а удаленные компоненты отсутствуют, вполне приемлемым может оказаться окно даже с увеличивающимся уровнем боковых лепестков, но зато с очень узким главным лепестком, что иллюстрирует рис. 11, в. Если динамический диапазон сигнала ограничен, то характеристики боковых лепестков не имеют особого значения, и поэтому можно выбрать окно, которое проще для численной реализации. Если спектр сигнала относительно гладок, то можно вообще не применять окна. Окна, которые могут сами в некотором смысле регулироваться, или «адаптироваться», к параметрам данных.
Практическая часть
Методика синтеза НРФ методом весовых функций [5]
1. Если частота среза и ширина переходной полосы не заданы напрямую, необходимо по значениям граничных частот полос пропускания/подавления рассчитать частоты среза по (3). В качестве частот среза заданной частотной характеристики используют их расчетные значения ωс, смещенные в полосу задерживания примерно на половину переходной полосы фильтра Δωпер. Это связано со свойственным данному методу размыванием границ перехода от полосы пропускания фильтра к полосе задерживания.
2. Если затухание частотной характеристики в полосе задерживания (максимальная неравномерность АЧХ в полосе подавления δ2) задана в долях коэффициента передачи, то по (5) пересчитать ее в логарифмический масштаб.
3. Определить, если не задана, ширину переходной полосы Dωпер = |ωЗ - ωП|min.
4. По полученному (заданному) значению затухания частотной характеристики в полосе задерживания A с помощью табл. П3, П4 или П5 Приложения выбирается тип весовой функции, отвечающей условию |δ2max |, дБ ≥ A, дБ, при минимальном значении ширины ее главного лепестка, т. е. параметра D. При использовании весовой функции Кайзера по табл. П6 Приложения находятся соответствующие заданному затуханию A параметры данной весовой функции β и D. При этом нужно учитывать, что расчетное значение затухания зависит от вида АЧХ синтезируемого фильтра, его граничных частот и длины весовой функции N и может оказаться как больше, так и меньше оценочного значения δ2max. Чем сложнее АЧХ фильтра (ПФ, ЗФ, многополосный фильтр (МПФ)), тем меньше затухание для одной и той же весовой функции. Это же относится и к неравномерности АЧХ в полосе пропускания.
5. Для выбранной (или заданной) весовой функции и рассчитанной (заданной) переходной полосе частотной характеристики фильтра Dωпер в соответствии с приближенным соотношением ΔωГЛ = Dωпер = D ωд/ N (ΔωГЛ - ширина главного лепестка спектральной плотности) определяется порядок фильтра (длина весовой функции/длина импульсной характеристики фильтра):
N ≥ D ωд/Dωпер или N ≥ D ωд/ΔωГЛ,
где D – коэффициент (D -фактор), зависящий от типа весовой функции (см. табл. П4 – П6 Приложения).
Значение N приравнивается ближайшему целому числу, обычно нечетному.
6. С помощью обратного преобразования Фурье 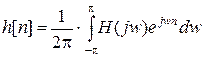 (8) или по более удобным формулам приведенных ниже (при рассмотрении синтеза фильтров конкретных типов – ф. 39, 45, 49, 53) аналитических выражений вычисляется смещенная вправо импульсная характеристика h з[ n − K ], n = 0… N −1, K = (N − 1)/2 соответствующая заданной частотной характеристике H з(j ω).
(8) или по более удобным формулам приведенных ниже (при рассмотрении синтеза фильтров конкретных типов – ф. 39, 45, 49, 53) аналитических выражений вычисляется смещенная вправо импульсная характеристика h з[ n − K ], n = 0… N −1, K = (N − 1)/2 соответствующая заданной частотной характеристике H з(j ω).
7. Находится импульсная характеристика фильтра путем весового усечения смещенной вправо на (N − 1)/2 отсчетов импульсной характеристики h [ k ] путем умножения на функцию окна v [ n ] (весовую функцию) (см. Приложение 2):
b [ n ]= h З[ n - K ] v [ n ], n = 0, 1,..., N − 1.
8. Рассчитывается АЧХ фильтра  или по более удобной формуле
или по более удобной формуле  и проверяется ее соответствие исходным данным по неравномерности частотной характеристики в полосе пропускания R и затуханию в полосе задерживания A.
и проверяется ее соответствие исходным данным по неравномерности частотной характеристики в полосе пропускания R и затуханию в полосе задерживания A.
9. Так как данный метод не обеспечивает точного соответствия исходных и расчетных данных (является итерационным), при необходимости корректируются значения расчетных частот среза ωС и порядка фильтра N и расчеты повторяются.
10. Находится минимально необходимая разрядность значений импульсной характеристики h [ n ] (коэффициентов фильтра, реализуемого на основе дискретной свертки), при которой расчетная АЧХ еще удовлетворяет заданным требованиям.
11. Выбирается способ реализации НРФ (дискретной свертки, ДПФ или частотной выборки) и решаются соответствующие ему задачи реализации.
Следует отметить, что метод весовых функций обеспечивает строгую линейность ФЧХ и постоянство группового времени запаздывания фильтра ввиду четной или нечетной симметрии получаемой этим методом импульсной характеристики h [ n ] = h [ N - l - n ].
Синтез ФНЧ
Рассмотрим сначала применение описанной методики для синтеза нерекурсивных ФНЧ, а затем распространим полученные результаты на синтез остальных нерекурсивных фильтров.
Заданная частотная характеристика идеального цифрового ФНЧ (рис. 1 а) определяется соотношением
 . .
| (33) |
Используя разложение в ряд Фурье частотной характеристики (33), определим импульсную характеристику НРФ
 . .
| (34) |
Учитывая, что H З(ω) является четной функцией частоты перепишем (34) в виде
 . .
| (35) |
Для ФНЧ после подстановки (33) в (35) и выполнения интегрирования получаем
| h З[0]= w с/π; h З[ n ]= sin(w с n)/π n, n = ±1, ±2, ±3,… | (36) |
Импульсная характеристика (36) определена при любых, целых значениях n и является бесконечной. Физически реализуемый НРФ обладает конечной импульсной характеристикой. Поэтому необходимо ограничить значения n. Пусть | n | ≤ K, где K = (N -1)/2 для фильтров с нечетными значениями N и K = N /2 для фильтров с четными значениями N. Тогда импульсная характеристика, соответствующая (36), запишется в виде

| (37) |
Импульсная характеристика (37) является некаузальной, так как имеет ненулевые значения при n < 0. Чтобы получить каузальную характеристику, необходимо задержать h НК[ n ] на K тактов, т.е.
| h К[ n ] = h НК[ n - K ], 0 ≤ n ≤ N -1. | (38) |
С учетом этого задержанная на K тактов характеристика
h К[ K ] = w с/π; 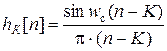 , 0 ≤ n ≤ N -1. , 0 ≤ n ≤ N -1.
| (39) |
где w с – нормированная частота среза. Нормирование по частоте проведем по (2а).
После перемножения h К[ n ] и дискретизированной функции требуемого окна v [ n ], получим коэффициенты b [ n ] для ФНЧ.
Для проверки АЧХ на соответствие заданной, необходимо ее рассчитать
по  , или по , или по
 , или по , или по
 . .
| (40) |
При расхождении результата с заданными условиями процесс расчета повторить, внеся соответствующие коррективы.
Синтез ФВЧ
Частотная характеристика идеального ФВЧ описывается соотношением
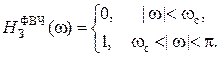
| (41) |
Данная характеристика является обратной по отношению к частотной характеристике идеального ФНЧ  и может быть представлена в виде
и может быть представлена в виде
 . .
| (42) |
Выражению (42) соответствует следующее соотношение импульсных характеристик ФВЧ и ФНЧ
 , ,
| (43) |
где δ[ n ]- единичная импульсная функция. Подставив в (43) выражение (36), получим
 ; ;
 , n = ±1, ±2, ±3,. , n = ±1, ±2, ±3,.
| (44) |
Аналогично рассуждая насчет усечения и сдвига на K, как и для ФНЧ, получим расчетные выражения, соответствующие (39) для ФВЧ:
h К[ K ] =1 – w с/π;  , 0 ≤ n ≤ N -1. , 0 ≤ n ≤ N -1.
| (45) |
Умножив h К[ n ] на требуемую функцию окна, получим коэффициенты импульсной характеристики b [ n ] для ФВЧ.
Расчет АЧХ ФВЧ ведется по тем же формулам (40), что и для ФНЧ
Синтез ПФ
Частотная характеристика идеального полосно-пропускающего фильтра может быть представлена в виде разности частотных характеристик двух идеальных ФНЧ с различными частотами среза ω1 и ω2 (ω1 < ω2)
 . .
| (46) |
Выполнив разложение в ряд Фурье частотной характеристики (46), получим выражение, определяющее импульсную характеристику ПФ
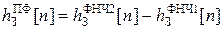 . .
| (47) |
С учетом (36) выражения (47) можно переписать в виде
 ; ;
 , n = ±1, ±2, ±3,.. , n = ±1, ±2, ±3,..
| (48) |
Аналогично р
Date: 2016-05-23; view: 8426; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |