Математическое ожидание и его свойства

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.

X			…
P			…

Т.е., если сл. величина имеет закон распределения, то

называется её математическим ожиданием. Если сл. величина имеет бесконечное число значений, то математическое ожидание определяется суммой бесконечного ряда , при условии, что этот ряд абсолютно сходится (в противном случае говорят, что математическое ожидание не существует).

Для непрерывной с л. величины, заданной функцией плотности вероят­ности f(x), математическое ожидание определяется в виде интеграла

при условии, что этот интеграл существует (если интеграл расходится, то говорят, что математическое ожидание не существует).

Пример 1. Определим математическое ожидание случайной величины распределённойпозакону Пуассона. По определению

или обозначим

,

Значит, параметр , определяющий закон распределения пуассоновской случайной величины равен среднему значению этой величины.

Пример 2. Для случайной величины, имеющей показательный закон распределения , математическое ожидание равно

( ):

(в интеграле пределы взять, с учётов того. что f(x) отлична от нуля только при положительных x).

Пример 3. Случайнаявеличина, распределенная по закону распределения Коши, не имеет среднего значения. Действительно

Свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной равно самой этой постоянной.

Постоянная С принимает это значение с вероятностью единица и по определению М(С)=С×1=С

Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.

Ограничимся доказательством этого свойства только для суммы двух дискретных случайных величин, т.е. докажем, что

Под суммой двух дискретных сл. Величин понимается сл. Величина, которая принимает значения с вероятностями

По определению

Но

где вероятность события , вычисленная при условии, что . В правой части последнего равенства перечислены все случаи появления события , поэтому равна полной вероятности появления события , т.е. . Аналогично . Окончательно имеем

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

У			…
Q			…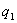
Х			…
Р			…

Приведем доказательства этого свойства только для дискретных величин. Для непрерывных случайных величин оно доказывается аналогично.

Пусть Х и У независимы и имеют законы распределения

Произведением этих случайных величин будет случайная величина, которая принимает значения с вероятностями равными, в силу независимости случайных величин, . Тогда

Следствие. Постоянныймножитель можно выносить за знак матема­тического ожидания. Так век постоянная С не зависит от того какое значение примет сл. величина X, то по свойству 3. имеем

М(СХ)=М(С)×М(Х)=С×М(Х)

Пример. Если a и b постоянные, то М(ах+b)=аМ(х)+b.

Математическое ожидание числа появления события в схеме независимых испытаний. П усть производится n независимых опытов, ве­роятность появления события в каждом из которых равна Р. Чис­ло появлений события в этих n опытах является случайной величиною Х распределённой по биномиальному закону. Однако, непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно: Число появления события в n опытах состоит изчисла появлений события в отдельных опытах, т.е.

где имеет закон распределения (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).

Р	1-р	р

Поэтому

или

т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность появления события в одном опыте.

Например, если вероятность попадания в цель при одном выстреле равна 0,1, то среднее число попадания в 20 выстрелах равно 20×0,1=2.

Date: 2016-05-23; view: 499; Нарушение авторских прав