
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розрахунок стержнів на розтяг і стиск
Міністерство освіти і науки України Державний заклад
«Луганський національний університет імені Тараса Шевченка»
КОЗУБ Ю. Г.,
ОПІР МАТЕРІАЛІВ
Методичні рекомендації
для організації самостійної роботи студентів спеціальності «Професійна освіта» напрямків підготовки
«Експлуатація та ремонт місцевого та автомобільного транспорту» і «Механізація сільськогосподарського вироб- ництва і гідромеліоративних робіт»
всіх форм навчання
ЗМІСТ
Вступ......................................................................................................................... 4
Питання до курсу................................................................................................... 5
1 модуль
1. Розрахунок стержнів на розтяг і стиск........................................................ 8
Контрольне завдання 1...................................................................................... 12
2. Статично невизначні конструкції............................................................... 14
Контрольне завдання 2...................................................................................... 17
3. Геометричні характеристики плоских перерізів..................................... 19
Контрольне завдання 3...................................................................................... 23
2 модуль
4. Плоский напружений стан........................................................................... 25
Завдання 4............................................................................................................. 28
5. Кручення............................................................................................................ 32
Контрольне завдання 5...................................................................................... 36
6. Згин балки. Підбір і перевірка перерізу балок......................................... 39
Контрольне завдання 6...................................................................................... 44
Додатки................................................................................................................. 56
Література............................................................................................................. 60
Вступ
Опір матеріалів – наука про методи розрахунку на міцність, жорсткість і стійкість елементів інженерних конструкцій. Без глибокого розуміння цих методів неможливе створення безпечних, довговічних і, що дуже важливо, економічних конструкцій.
Опір матеріалів історично вважається найбільш складною дис- ципліною технічного циклу. Причиною тому є дуже широкий круг пи- тань, що вивчаються в рамках курсу. Крім того, опір матеріалів базуєть- ся на таких фундаментальних дисциплінах, як математика, фізика і тео- ретична механіка, тобто вимагає серйозної базової підготовки.
Мета курсу «Опір матеріалів» - теоретично і практично підготу- вати майбутніх фахівців в області проектних розрахунків конструкцій та їх частин; навчити їх проектувати та вибирати деталі, які б працювали в заданих умовах протягом необхідного часу, забезпечивши при цьому максимальну економію енергетичних ресурсів і матеріалів.
Невід’ємною і дуже важливою складовою сучасної системи осві- ти є самостійна робота студентів. Саме організації самостійної роботи присвячене це видання. Самостійна робота при вивченні опору матеріа- лів полягає в індивідуальному розв’язанні найбільш типових практич- них задач.
Методичні вказівки мають зорієнтувати студентів при вивченні курсу, сприяти більш швидкому засвоєнню матеріалу. До видання включено 12 завдань з найбільш практично важливих розділів дисцип- ліни. На початку кожного завдання надано теоретичні відомості, той мінімум, без якого неможливе успішне вирішення даної задачі. Кожне завдання супроводжується детальними прикладами вирішення подібної задачі та рекомендаціями до розв’язання. Контрольні питання, що наве- дені в кінці кожного завдання, мають вказати студентам на пріоритетні питання при підготовці до контрольно-модульної роботи.
Додаток в кінці рекомендацій дозволяє приступати к вирішенню задач не користуючись довідниковою літературою. За додатком наве- дено перелік використаної і рекомендованої авторами літератури, якої цілком достатньо не тільки для успішного розв’язання задач, а й для якісної підготовки добудь-яких форм контролю знань.
Курс «Опір матеріалів » вивчається в 4 - 5 семестрах студентами денної форми навчання, і в 5 семестрі студентами заочної форми на- вчання. За один семестр студенти стаціонару самостійно виконують 6 задач – по три до кожного модулю. На заочному відділенні задачі є до- пуском до екзамену, їх кількість визначається викладачем, але має ста- новити не менше 6 задач.
Питання курсу
1. Завдання курсу та його зв'язок з іншими дисциплінами.
2. Основні гіпотези про деформоване тіло.
3. Лінійні та кутові деформації та переміщення.
4. Пружність та пластичність. Твердість.
5. Поняття ізотропії та анізотропії.
6. Зовнішні сили, їх класифікація.
7. Метод перерізів. Внутрішні сили в перерізі.
8. Повна, нормальна і дотична напруги.
9. Поняття про напружений стан і його види.
10. Визначення елементів, які вивчаються в курсі.
11. Традиційні та нові матеріали, які застосовуються для конструкцій.
12. Закон Гука. Модуль пружності першого роду.
13. Зв'язок між повздовжніми і поперечними деформаціями. Коефі- цієнт Пуассона.
14. Діаграма напружень при розтягу сталі. Її характерні точки.
15. Діаграма напружень при стиску сталі. Її характерні точки.
16. Коефіцієнт запасу міцності. Підбір перерізів.
17. Врахування власної ваги. Бруси рівного опору розтягу і стиску.
18. Статично невизначувані задачі на розтяг або стиск.
19. Вплив температури та неточності виготовлення.
20. Розрахунок гнучкої ниті.
21. Напруження в похилих перерізах бруса (стержня) при лінійно- напруженому стані.
22. Напруження в похилих перерізах бруса (стержня) при плоско- напруженому стані.
23. Дослідження плоского напруженого стану за допомогою кругів Мору.
24. Максимальне дотичне напруження. Закон парності дотичних напруг.
25. Поняття про головні напруження.
26. Визначення лінійних деформацій для загального випадку на- пруженого стану.
27. Узагальнений закон Гука. Зміна об’єму тіла.
28. Загальні поняття про гіпотези міцності.
29. Перша, друга і третя класичні теорії міцності.
30. Теорія міцності Мора.
31. Поняття про нові теорії міцності.
32. Явища, що ускладнюють розрахунок на міцність: концентрація напруг, вплив температури на механічні властивості.
33. Статичний момент площі. Осьові, відцентрові і полярні момен- ти інерції. Радіуси інерції.
34. Залежності між моментами інерції для паралельних осей, їх зміна при повороті координатних осей.
35. Головні осі і моменти інерції, їх знаходження.
36. Моменти інерції складних профілів. Моменти опору.
37. Явища зсуву. Дотичні напруги.
38. Закон Гука для зсуву. Модуль зсуву.
39. Розрахунок на міцність при зсуві.
40. Розрахунок заклепочних з’єднань.
41. Розрахунок зварних з’єднань.
42. Гіпотези деформації кручення прямого бруса круглого поперечно- го перерізу.
43. Напруження в поперечному перерізі. Кут закручування.
44. Потенціальна енергія деформації при крученні.
45. Побудова епюр крутячих моментів та напружень.
46. Побудова епюри кутів закручування.
47. Статично невизначені задачі при крученні.
48. Опори і опорні реакції балки. Зовнішні сили, які викликають згин.
49. Внутрішні силові фактори у поперечних перерізах балки при згині.
50. Диференціальні залежності між згинаючим моментом, попереч- ною силою та інтенсивністю розподіленого навантаження.
51. Побудова епюр поперечних сил і згинаючих моментів.
52. Нормальні і дотичні напруження при чистому згині.
53. Головні напруження при згині. Раціональні перерізи балок.
54. Складні балки і балки змінного поперечного перерізу.
55. Прогини та кути повороту.
56. Диференціальне рівняння зігнутої осі балки.
57. Методи визначення деформацій балок при згині.
58. Балки однакового опору згину, їх деформації.
59. Потенціальна енергія при різних видах деформацій.
60. Теорема Кастильяно. Спосіб введення додаткової сили.
61. Теорема Максвела-Мора. Спосіб Верещагіна.
62. Теорема взаємності робот і переміщень.
63. Статично невизначувані балки та рами. Вибір основної системи.
64. Кінематичний і структурний аналіз невизначуваної рами.
65. Теорема про три моменти та її застосування.
66. Метод сил та його застосування до розрахунку статично неви- значуваних балок та рам.
67. Косий згин, загальні відомості.
68. Одночасна дія згину і розтягу, чи стиску.
69. Позацентровий розтяг або стиск, ядро перерізу.
70. Одночасна дія згину і кручення, результуючі моменти. Побудо- ва епюр.
71. Розрахунок валів, одночасно працюючих на згин і кручення.
72. Поняття про стійкість. Критична сила.
73. Формула Ейлера для критичної сили.
74. Гнучкість стержня та вплив способів закріплення на величину сили.
75. Розрахунок на стійкість стиснених стержнів.
76. Криві бруси, особливості їх розрахунку.
77. Динамічна дія навантажень. Врахування сил інерції при рівноп- рискореному русі.
78. Пружні коливання. Вільні і вимушені коливання.
79. Власні коливання систем з лінійним затуханням.
80. Частота і період коливань. Явище резонансу й його значення в техніці.
81. Критична кількість обертань валу.
82. Напруження при пружному ударі.
83. Розтягуючий, скручуючий та згинаючий удари.
84. Поняття про хвильову теорію удару.
85. Механічні властивості матеріалів при ударі.
86. Втомленість матеріалів.
87. Загальні характеристики циклу і межа втомлюваності.
88. Розрахунок матеріалів на витривалість.
89. Коефіцієнт запасу міцності при втомленості матеріалів, його визначення.
90. Поняття про малоциклову втомленість матеріалів.
91. Фактори, що впливають на втомленість матеріалів: концентра- ція напруг, масштабний ефект, якість обробки поверхні.
92. Загальні поняття механіки руйнування.
93. Крихке руйнування задача Гриффитса.
94. Історія створення і розвитку композиційних матеріалів.
95. Класифікація композиційних матеріалів.
96. Характеристики міцності односпрямованих композиційних мате- ріалів.
97. Переваги та недоліки сучасних композиційних матеріалів.
98. Визначення власних частот коливань пружних систем.
99. Поняття про чисельні методи розрахунку в опорі матеріалів.
100. Сучасні проблеми опору матеріалів.
МОДУЛЬ 1
Розрахунок стержнів на розтяг і стиск
Теоретичні відомості
Поздовжня сила в довільному перетині стержня чисельно дорів- нює алгебраїчній сумі проекцій на його поздовжню вісь всіх зовнішніх сил, прикладених до залишеної частини:
N = å Pi.
çàëèø
(1.1)
Вважається, що сила, яка розтягує - додатна, а яка стискує - від’ємна. У будь-якому перерізі стержня під дією поздовжніх сил виникає нормальне напруження, яка обчислюється за формулою:
 o = N
o = N
F
(1.2)
Якщо враховувати власну вагу стержня, то поздовжня сила на ос- нові методу перерізів визначається по формулі:
N (x) = N + g F x,
(1.3)
де F - площа поздовжнього перерізу; г - питома вага, х - координата перерізу по довжині стержня від вільного кінця.

 Максимальна поздовжня сила, вочевидь, буде рівна за x = l:
Максимальна поздовжня сила, вочевидь, буде рівна за x = l:
де l – довжина стержня.
N (x)
max= N + g Fl, (1.4)
Умова міцності має вигляд:
S
а з урахуванням власної ваги
max
= N £ [ s ], (1.5)
F
s max
= N + g l £ [ s ], (1.6)
 F
F
де [у] - напруження, що допускається для матеріалу, з якого виготовле- ний стержень. Тоді з умови міцності можна обчислити необхідну площу перерізу стержня:
 F ³ N
F ³ N
[ s ]
, F ³
N
 [ s ]- g l.
[ s ]- g l.
(1.7)
Якщо зовнішні сили відсутні, то умова міцності запишеться у ви-
гляді:
gl £ [ s ].
(1.8)
Звідси гранична довжина, при якій стержень не повинен руйнува- тися від дії власної ваги
lгр =
[ s ]

G
. (1.9)
Переміщення будь-якого перерізу, що знаходиться на відстані x від вільного кінця стержня, до якого прикладена зовнішня сила Р, з вра- хуванням власної ваги, визначається по формулі:
l
l (x) = ò
N ( x ) l ( P + gFx ) dx dx = ò =
P ( l - x ) g
 +
+
(l 2
- x 2)
. (1.10)
x EF x EF
EF 2 E
Якщо власну вагу не враховувати, то другий доданок в рівнянні (1.10) відкидають. В тому випадку, якщо сила Р прикладена на якійсь відстані від кінця стержня, його розбивають на ділянки і переміщення обчислюють на кожній з ділянок.
Переміщення нижнього кінця стержня, дорівнюватиме повному подовженню стержня і визначиться формулою
D l = l (x)
= Pl + g l
. (1.11)


Якщо стержень був розбитий на ділянки, то повне подовження обчислюється як сума переміщень кожної ділянки
n
D l = åD li. (1.12)
i =1
Умова жорсткості має вигляд
D l £ [D l ],
де [Д l ] – подовження стержня, що допускається. Площу поперечного перерізу стержнів розраховують з умов міцності і жорсткості, а потім беруть найбільше значення.
Рекомендації до розв’язання задачі №1
При вирішенні завдань на розтяг-стиск стержнів необхідно ма- ти на увазі наступне:
1. У будь-якому перерізі стержня (бруса) при розтягу чи стиску ви- никає лише один силовий чинник – поздовжня сила N, яка ви- значається методом перерізів.
2. Передбачається, що нормальне напруження по перерізу розподі- лена рівномірно і обчислюються за формулою (1.2).
3. Для побудови епюр необхідно заздалегідь розбити стержень (брус) на ділянки, межі яких визначаються точками, де приложені силові чинники чи змінюються розміри поперечного перерізу.
4. При визначенні переміщення перерізів ступінчастих стержнів по формулі (1.10) слід враховувати, що площа F змінюється.
5. Епюри переміщень з урахуванням власної ваги на ділянках мають квадратичний характер, а при дії на стержень (брус) лише зосереджених сил – лінійний.
Приклад розв’язання задачі №1
Побудувати епюри поздовжніх сил, нормальних напружень і пе- реміщень для ступінчастого бруса (рис.1).
Розбиваємо брус на ділянки (рис.1, а) починаючи від вільного кі- нця. Будуємо епюри поздовжніх сил (рис. 1, б) і нормальних напружень (рис. 1, в). Для цього, застосовуючи метод перерізів, залишаємо праву частину і відкидаємо ліву на кожній ділянці бруса. Це дозволяє не ви- значати реакцію в опорі. Маємо:
NI = P 1 = P; NII = NI;
NIII = P 1 - P 2 = P - 2 P = - P;
NIV
= NIII;
NV = P 1 - P 2 + P 3 = P - 2 P + 4 P = 3 P.
На кожній з ділянок визначаємо нормальне напруження, підставля- ючи значення сил в ньютонах, а площ в м2. Маємо:
o I = NI / F 1 = P / 2 F; s II = NII / F 2 = P / F;
o III = NIII / F 2 = - P / F; s IV = NIV / F 3 = - P / 2,5 F;
sV = NV / F 3 = 3 P / 2,5 F.
Для побудови епюри переміщень досить визначити переміщення перерізів, що співпадають з кордонами ділянок, оскільки між ними епюра лінійна.
Переріз А не зміщується, тобто
lÀ = 0.
Побудову епюр переміщень слід завжди починати від нерухомого або умовно прийнятого нерухомим перерізу.
Переміщення перерізу В дорівнює подовженню ділянки АВ (ді- лянки V) бруса:
l = D lV
= NVl E × 2,5 F
= 3 Pl

 E × 2,5 F
E × 2,5 F
= 1,2 Pl.
EF
Переріз В зміщується вправо. Відповідну ординату вважаємо до- датною і відкладемо (у вибраному масштабі) вгору по осі епюри (рис. 1, г).

Рис.1. Побудова епюр
Переміщення перерізу С дорівнює алгебраїчній сумі змін довжин ділянок V і IV бруса:
Аналогічно
lС = lВ
+ D lIV
= 1,2 Pl
EF
- Pl
 E 2,5 F
E 2,5 F
= 0,8 Pl.
EF
lD = lC
+ D l
III
= 0,8 Pl - Pl
EF EF
= -0,2 Pl.
EF
Знак мінус вказує, що переріз D переміщується вліво (оскільки раніше було прийнято рахувати переміщення вправо додатним). Далі
lK = lD
+ D lII
= -0,2 Pl +
EF
Pl = 0,8 Pl;
EF EF
lM = lK
+ D lI
= 0,8 Pl +
EF
Pl
 E 2 F
E 2 F
= 1,3 Pl.
EF
Будуємо епюру переміщень (рис. 1, г).
Контрольне завдання № 1
Таблиця №1
| № варіант | Зусилля в точці, кН | Довжини ділянок стер- жня, м | Діаметри стержня, м | № схеми | ||||||||||||
| PА | PВ | PС | PD | PE | PF | a | b | c | d | e | f | D1 | D2 | D3 | ||
| -100 | - | 0,5 | 0,7 |
Виконати розрахунок стержня від дії зосереджених сил, якщо модуль
пружності стержня Е = 2,2∙105 МПа, щільність g
а) без урахування власної ваги стержня;
= 7.8 ×10 4 H / м 3:
б) з урахуванням власної ваги при постійному діаметром D2 стержня.
Розв’язання задачі виконати в наступній послідовності:
1. Накреслити стержень в масштабі по заданих розмірах і докласти зусилля у вказаних точках (додатними вважати значення зусиль що розтягують, від’ємними - що стискають);
2. Побудувати епюру поздовжніх сил;
3. Побудувати епюру нормального напруження;
4. Побудувати епюру переміщень поперечних перерізів;
5. Оцінити міцність стержня на розтяг і стиск.
Напруга, що допускається на розтяг [ур] = 160 МПа, на стиск [уст] = 100 МПа. Дані узяти з таблиці 1.
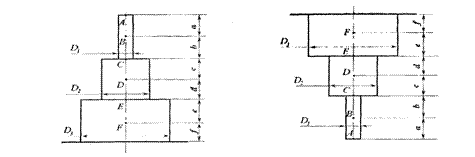 |
Схема 1 Схема 2
Контрольні питання
1. Як виглядає умова міцності при деформації розтягу-стиску, які завдання вона вирішує?
2. Що станеться з конструкцією при порушенні умови міцності?
3. В чому полягає суть коефіцієнту запасу міцності.
4. Для чого використовують метод перерізу в стержнях.
5. Яким чином обчислюється поздовжня сила, нормальне напру- ження і деформація?
6. Залежно від яких чинників стержень ділиться на ділянки?
2. Статично невизначні конструкції
Теоретичні відомості
Статично невизначними називаються конструкції, в елементах яких зусилля не можуть бути визначені тільки з рівнянь статики. Окрім рівнянь статики при вирішенні статично невизначних завдань необхідно використовувати також рівняння, що враховують деформації елементів конструкцій.
Всі статично невизначні конструкції мають так звані зайві зв'яз- ки. «Зайвими» такі зв'язки називаються тому, що вони не є необхідними для забезпечення рівноваги конструкції і її геометричної незмінності, а обумовлені вимогами до міцності і жорсткості конструкції. Кількість зайвих невідомих, або міра статичної невизначності системи являє со- бою різницю між числом невідомих, що підлягають визначенню, і чис- лом рівнянь статики.
При розрахунку статично невизначних конструкцій на міц- ність використовується нерівність:
s £ s
s
= гр
max
[ ],
П
де [ у ] - напруга, що допускається, угр - гранична напруга, [ n ] - норма- тивний коефіцієнт запасу міцності.
Умова жорсткості, як і в разі розрахунку статично визначних конструкцій, має вигляд
D l £ [D l ].
Згідно умовам міцності і жорсткості виділяють задачі трьох типів:
1) підбір параметрів стержня, які забезпечать роботу при заданих наван- таженнях; 2) перевірка існуючої конструкції на міцність і жорсткість; 3) визначення допустимих напружень за заданим коефіцієнтом запасу.
Рекомендації до розв’язання задачі №2
1. Знаходять міру статичної невизначності n.
2. Складають рівняння рівноваги відсічених елементів конструкції, що містять невідомі зусилля (статична сторона завдання).
3. Встановлюють зв'язок між деформаціями окремих елементів конс- трукції, виходячи з умов спільності деформацій. Отримані рівняння називаються рівняннями сумісності деформацій (геометрична сторона завдання).
4. У рівняннях сумісності виражають деформації елементів із закону Гуку через невідомі зусилля, що діють в них (фізична сторона завдання).
5. Вирішують спільно отримані рівняння відносно шуканих невідомих зусиль (задача синтезу).
Приклад розв’язання задачі №2
Для стержня ступінчастого поперечного перерізу, закладеного по кінцях (рис. 2,а), перевірити міцність:
1) з урахуванням силового навантаження силою Р = 6кН;
2) при охолоджуванні стержня на 10єС за умови, що сила відсутня. Прийняти F1 = 10 см2, l1 = 4 м, l2 = 2 м, l3 = 2 м, Е = 2∙105 МПа, коефіцієнт теплопровідності б = 10∙10-6 град-1, допустиме напруження [у] = 160 МПа.
 |
1). Дана система є один раз статично невизначною: дві реакції в точках А і В і одне рівняння статики.
|
Підставивши перше рівняння в друге, знаходимо невідому силу
 X = P (l 1 + 2 l 2) (l 1 + 2 l 2 + 2 l 3)
X = P (l 1 + 2 l 2) (l 1 + 2 l 2 + 2 l 3)
= 6 × (4 + 2 × 2)
 (4 + 2 × 2 + 2 × 2)
(4 + 2 × 2 + 2 × 2)
= 4(кН).

 Розбиваємо конструкцію на три ділянки і визначаємо
Розбиваємо конструкцію на три ділянки і визначаємо
N 1 = N 2 = -6 кН + 4 кН = -2 кН, N 3 = 4 кН.
Тепер будуємо епюру поздовжніх сил N (рис. 3,а). Далі знаходимо напруження в перерізах стержня

= -1 МПа,
1 2 ×10-3
3 3
 s =-2 ×10
s =-2 ×10
2 10-3
= -2 МПа, s 3
Times;10
 10-3
10-3
= 4 МПа.
За отриманими результатами будуємо епюру нормальних напружень (рис. 3,б). Найбільше напруження виявилось менше допустимого [у] = 160 МПа. Отже, міцність стержня забезпечена.
2). При розв’язанні температурної задачі виберемо основну систему, зображену на рис. 4. Умова еквівалентності систем

Рис. 4. Основна система
D lB = 0.
З іншого боку переміщення точки В повинне складатися з тем- пературного подовження і подов- ження за рахунок деформації від сили Х1.
D lВ
= D lt
+ D lx
= a (l 1
+ l 2
+ l 3)D t +
X 1 l 1
 2 EF 1
2 EF 1
+ X 1 (l 2 + l 3) =
 EF 1
EF 1
|
 Розбиваємо стержень на дві ділянки в місцях зміни поперечного перерізу. На кожній із ділянок поздо- вжня сила
Розбиваємо стержень на дві ділянки в місцях зміни поперечного перерізу. На кожній із ділянок поздо- вжня сила
 |
N 1 = N 2 = X 1 = -32 (кН).
Рис. 5а. Епюра поздовжніх сил Рис. 5б. Епюра нормальних напружень
s = N 1
Times;10
= N 2 =- 32 ×10
= -32.

2 ×10-3



МПа
За результатами розрахунків будуємо епюри N і у (рис. 5,а і б).
Найбільше напруження виявилось менше допустимого [у] = 160 МПа. Отже, міцність стержня забезпечена.
Контрольне завдання № 2
Для заданої схеми вантаження стержня потрібно:
1. Побудувати епюру поздовжніх сил N, напружень у і переміщень л від дії зосередженої сили Р.
2. Побудувати епюру поздовжніх сил, напружень і переміщень, якщо брус нагрівається на ДТ градусів за відсутності сили Р.
Коефіцієнт лінійного розширення б =12∙10-61/град, модуль пруж- ності Е = 2∙105 МПа. Дані узяти з таблиці 2.
Таблиця 2.
| № варіанту | № схеми (рис. 6 ) | F, см2 | а, м | в, м | с, м | DТ, град | Р, Н |
| 2,4 | 1,5 | 2,3 |

Рис. 6. Схеми до задачі 2
Контрольні питання.
1. Які системи називаються статично невизначними?
2. Що таке умова спільності деформацій і як вона формулюється?
3. Запишіть умови міцності і жорсткості.
4. Що таке коефіцієнт запасу міцності?
3. Геометричні характеристики плоских перерізів
Теоретичні відомості
Статичним моментом плоского перерізу відносно осі Ох нази- вається узята за всією площею перерізу сума добутків площ елементар- них ділянок на їх відстань до цієї осі, тобто
Sx = ò ydF. (3.1)
F
Аналогічно, статичний момент перерізу відносно осі Оу
Sy = ò xdF. (3.2)
F
Статичний момент має розмірність мм3, см3, м3.
Залежно від положення осі, відносно якої обчислюється статичний момент, він може бути додатним, від’ємним або рівним нулю. При відомих статичних моментах і площі перерізу координати його центру тяжіння визначаються по формулах
xС = Sy / F;ü
|
|
(3.3)
В разі відомих координат центру тяжіння статичні моменти ви- значають за формулами
Sx = FyC;ü
ý
S = Fx
y C. þ
(3.4)
У тих випадках, коли переріз може бути розбитий на прості скла- дові частини, площі і координати центрів тяжіння яких відомі, поло- ження центру тяжіння всього перерізу визначають по формулах

|
F 1 + F 2 +... + Fï
y = F 1 y 1 + F 2 y 2 +... + Fï yï,

|
(3.5)
де F 1, F 2,..., Fï
- площі окремих частин перерізу, а
x 1, x 2,..., xï и
y 1, y 2,..., yï
- координати центрів тяжіння кожної частини.
Осьовим моментом інерції плоского перерізу відносно даної осі Ох називається інтеграл добутків елементарних площ на квадрати їх відстаней до цієї осі
|
F
(3.6)
Аналогічно, момент інерції відносно осі
|
F
(3.7)
Сума осьових моментів інерції відносно двох взаємно перпенди- кулярних осей дорівнює полярному моменту інерції відносно початку координат.
J r = J X + JУ.
(3.8)
Відцентровим моментом інерції плоского перерізу називається інтеграл добутків елементарних площ на їх відстані до двох даних взаємно перпендикулярних осей
JXY
= ò yxdF. (3.9)
F
В процесі повороту осей відцентровий момент інерції змінюється без- перервно, а при деякому положенні осей він стає рівним нулю. Якщо осі проходять через центр тяжіння перерізу, то вони називаються централь- ними осями. Якщо відцентровий момент інерції відносно цих осей дорі- внює нулю, то вони називаються головними центральними осями і поз- начаються u і v. Осьовий і відцентровий моменти інерцій мають розмір- ність мм4, см4, м4.
Осьові моменти інерції відносно осей, що паралельні до головних
|
|
1 1
Відцентровий момент інерції відносно осей, що паралельні до го- ловних
|
|
1 1
(3.11)
де а, b – відстані від головних осей до паралельних.
При повороті центральних осей на кут б, який вважається додат- ним проти ходу годинникової стрілки, осьові і відцентровий моменти інерції набирають наступного вигляду:
|
|
|
|
JX 1 Y 1
= - JY - JX sin 2 a + J
 2 XY
2 XY
cos2 a
. (3.14)
Кут нахилу головних центральних осей (u, v) по відношенню до центральних осей (x, y) позначають б0 і його можна отримати, якщо прийняти праву частину рівняння (3.14) такою, що дорівнює нулю:
tg 2 a 0
= 2 J XY
 JY - J X
JY - J X
. (3.15)
Головні центральні моменти інерції відносно головних централь- них осей набувають екстремальних значень, величину яких можна об- числити, підставивши б0 з (3.15) в рівняння (3.12) і (3.13):
 1 [ ]
1 [ ]
Ju, v = J max =
min 2
(JY + J X) ±.
Рекомендації до розв’язання задачі №3
1. Переріз необхідно викреслити в масштабі 1:2, вказати всі розміри і осі.
2. При розв’язанні задачі, якщо переріз складний, його розбивають на прості складові частини.
3. Випадкові осі для складного перерізу доцільно проводити так, щоб усі часті складного перерізу мали додатні координати і при цьому, по можливості, торкалися сторін фігури.
4. Користуючись сортаментами (табл. 3 і 4 Додатку), необхідно прави- льно вибирати значення осьових і відцентрових моментів інерції. Для рівнобокого кутика значення відцентрового моменту інерції обчислю- ється за формулою:
JXY
= J max - J min
2
5. Слід мати на увазі, що вісь «min» пересікає значно більшу частину площі перерізу, чим вісь «max». Також, якщо JXY < 0, то вісь проходить через I і III квадрати, а якщо JXY > 0, то через II і IV.
Приклад розв’язання задачі №3
Для заданого таврового перерізу (рис. 7) визначити координати центра тяжіння, знайти осьові і відцентрові моменти інерції відносно випадкових осей, головні центральні моменти інерції.
Введемо випадкові осі u і v як показано на рис.7.
1. Визначаємо координати центра тяжіння фігури.
Якщо фігура має вісь симетрії, то координата центру тяжіння обов’язково знаходиться на ній. В даному випадку координату uС мо- жна визначити візуально з малюнка, вона рівна uС = 6 см. Для визначен-
ня координати vС розіб'ємо переріз на два прямокутники I і II, після чого визначимо центри тяжіння окремих частин і їх площі:
Знаходимо другу координату центра тяжіння фігури


|
F 1 + F 2
18 + 36
де v1 і v2 - відстань від осі u до центру тяжіння прямокутників. Через отриманий центр тяжіння фігури (6; 11) проводимо осі x і у - головні центральні осі перетину.

Рис. 7. Тавровий переріз
Обчислюємо моменти інерції кожного з прямокутників відносно власних центральних осей:
|
|
J II
= bh 3 /12 = 1,5×123 /12 = 216 см 4;
|
|
= b h 3 /12 = 12× 33 /12 = 27 см 4;
X 2 2 2
J II = h b 3 /12 = 3×123 /12 = 437 см 4.
У 2 2
Обчислимо моменти інерції кожного з прямокутників відносно головної осі x. Для прямокутника I:
a 1 = n C - n 1 = 11 - 6 = 5 см,
J I = J I + a 2 F = 216 + 52 ×12×1,5 = 666 см 4.
X X 1 1 1
Для прямокутника II:
a 2= n 2 - n C = 13,5 - 11 = 2,5 см;
J II = J II
+ a 2 F
= 27 + 2,52 ×12×3 = 252 см 4.
X X 2 2 2
Обчислюємо головні моменти інерції перерізу:
|
|
|
J = J II + J II = 3,38 + 437 = 440,38 см 4.
У У У
Головна вісь Оу збігається з центральними осями частин фігури, тому при обчисленні не знадобилося використовувати залежність між моментами інерції відносно паралельних осей.
Контрольне завдання №3
Для заданого поперечного перерізу, що складається з двох стан- дартних перерізів сортаменту (рис. 8, табл. 3), потрібно:
1) Визначити положення центру тяжіння;
2) Знайти осьові і відцентрові моменти інерції відносно випадкових осей (u і v), що проходять через центр тяжіння;
3) Визначити напрям головних центральних осей (х і у);
4) Знайти моменти інерції відносно головних центральних осей;
5) Викреслити перетин в масштабі 1:2 і вказати всі розміри і осі.

Рис. 8. Стандартні профілі
Таблиця 3
| № варіа- нту | Тип перерізу за рис. 8 | Швелер | Рівнобокий кутик | Двотавр |
| IV | 100´100´10 | - |
Контрольні питання.
1. Яка залежність між осьовими і полярними моментами інерції?
2. Дайте визначення головним центральним осям інерції перерізу?
3. Як встановити правильність визначення знаку відцентрового момен- ту інерції перерізу, несиметричного відносно його центральних осей?
МОДУЛЬ 2
Date: 2016-05-17; view: 3882; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |