Практическое занятие 4. Расчет параметров автоколебаний и анализ их устойчивости алгебраическим способом

Выражения для коэффициентов гармонической линеаризации типовых нелинейностей и примеры их вывода приводятся в литературе. Для решения задач в текущем семестре потребуются коэффициенты, представленные в таблице 2.1 для случая симметричных колебаний.

Пример 1.

Рассмотрим САУ, структурная схема которой представлена на рис. 29.

Пусть задающее воздействие g (t)=0. С учетом формы статической характеристики нелинейности отметим, что условия симметричности автоколебаний выполняются. Нелинейность однозначная. Коэффициенты гармонической линеаризации нелинейности: , q’ (a)=0.

Передаточная функция линейной части системы имеет вид:

,

, .

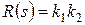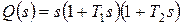Характеристический полином:

.

Составим уравнения (5.6)-(5.7):

;

, ;

;

, ;

, ;

, .

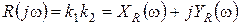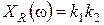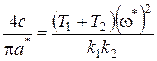В результате их решения находим один вариант параметров предельного цикла:

, .

Таблица 2.1

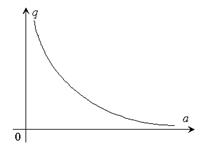
Статическая характеристика и уравнение нелинейности	Коэффициенты гармонической линеаризации	Зависимости коэффициентов от амплитуды колебаний
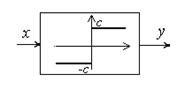
	, q’ (a)=0
	, , ,
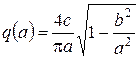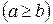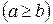
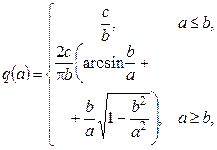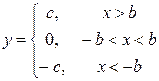
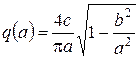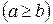	q’ (a)=0
	, , q’ (a)=0
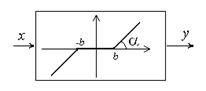
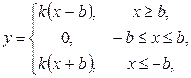k= tga	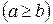, q’ (a)=0

Для проверки его устойчивости составим характеристический комплекс системы:

;

,

и проверим выполнение условия (5.12):

, ,

, ,

.

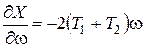Поскольку порядок исследуемой системы – третий, можно сделать вывод: в системе будет иметь место автоколебательный процесс с параметрами:

, .

Пример 2.

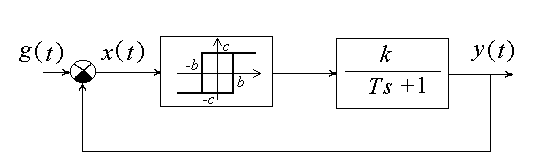
Исходные данные: g (t)=0.

Проанализировать возможность автоколебаний в системе.

Условия симметричности автоколебаний выполняются. Коэффициенты гармонической линеаризации нелинейности:

,

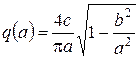существуют при a≥b.

Характеристический полином линеаризованной системы:

.

Составим уравнения для определения параметров автоколебаний:

,

,

.

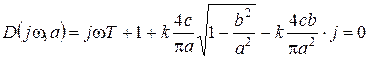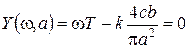Нетрудно видеть, что уравнение X (w, a)=0 не имеет решения в силу неотрицательности всех параметров системы и переменной a.

Метод гармонической линеаризации является приближенным. Корректность получаемых на его основе результатов определяется достоверностью допущения о наличии свойства фильтра у линейной части системы. Этот вопрос на основе рассмотренного примера подробно рассматривается в лабораторной работе №3.

Пример 3.

Исходные данные: g (t)=0; b =10; c =10; k=k ₁ k ₂=20 c^-1; T ₁=1 c; T ₂=0,1.

Проанализировать возможность автоколебаний в системе.

С учетом формы статической характеристики нелинейности отметим, что условия симметричности автоколебаний выполняются. Нелинейность однозначная. Коэффициенты гармонической линеаризации нелинейности: 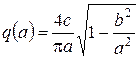, существует при a≥b, q’ (a)=0. Особо следует подчеркнуть: автоколебания при рассматриваемой нелинейности возможны только с амплитудой, превышающей ширину зоны нечувствительности.

Передаточная функция линейной части системы имеет вид:

,

, .

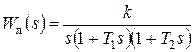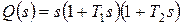Характеристический полином линеаризованной системы:

.

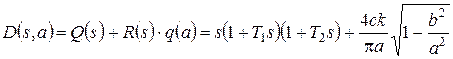Составим уравнения для определения параметров автоколебаний:

,

, ;

,

, ;

: ;

: .

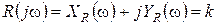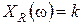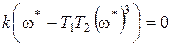В результате решения последнего уравнения находим частоту возможного предельного цикла:

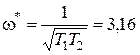c^-1.

Для определения амплитуды предельного цикла после подстановки найденной частоты получим следующее уравнение:

.

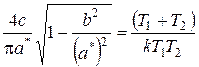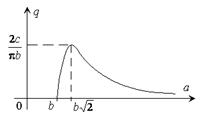
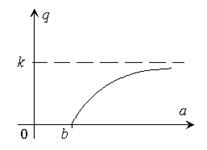
Зависимость q (a), показанная на рисунке, соответствует его левой части. Проводя через отметку на вертикальной линии, соответствующую значению правой части уравнения, горизонтальную прямую, можно решить уравнение графически.

Нетрудно убедиться, что данное уравнение имеет решения при выполнении условия:

или k≥k _гр, где с^-1.

При k=k _гр уравнение имеет одно решение .

При k>k _гр, что соответствует числовым условиям задачи, для нахождения двух значений амплитуды предельного цикла можно придти к биквадратному уравнению:

,

.

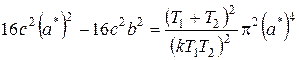После подстановки исходных данных задачи получим: a ₁=11,6; a ₂=20.

Для проверки устойчивости найденных предельных циклов составим характеристический комплекс системы:

,

,

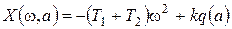и проверим выполнение условия устойчивости:

, ,

, ,

.

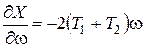Из рисунка видно, что для a=a ₁ , и определитель отрицателен, при a=a ₂ 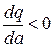, определитель положителен, то есть условие устойчивости предельного цикла выполняется для a=a ₂. Поскольку порядок исследуемой системы – третий, можно сделать вывод: предельный цикл с параметрами w=3,16, a= 20 устойчив. Необходимо отметить, что для рассматриваемой системы нельзя сделать общий вывод об устойчивом автоколебательном процессе, так как для нее имеется еще один – неустойчивый – предельный цикл c a=a ₁. Следовательно, в его окрестности имеет место колебательный процесс: при a>a ₁ расходящийся к устойчивому предельному циклу – автоколебаниям; при a<a ₁ сходящийся к состоянию равновесия. В таком случае говорят, что система асимптотически устойчива «в малом», то есть при исходных значениях фазовых координат внутри предельного цикла с амплитудой a= 11,6. При больших исходных значениях фазовых координат в системе устанавливаются автоколебания.

Для получения полной картины возможных вариантов процесса в рассматриваемой системе осталось выяснить характер процесса при k<k _гр. Для этого проанализируем характеристический полином. Необходимое условие устойчивости выполняется, так как q (a)>0 (см. рисунок). Применим критерий Гурвица и получим условие устойчивости:

,

.

Нетрудно убедиться с учетом характера функции q (a), что при k<k _гр данное условие будет выполнено, то есть система асимптотически устойчива.

Результаты выполненного анализа наглядно интерпретируются рисунком, где представлена зависимость амплитуды предельных циклов от коэффициента передачи линейной части системы. Стрелками показан характер изменения амплитуды колебаний при переходных процессах в системе в различных областях плоскости данных параметров.

При k _л < k _гр имеет место затухающий к состоянию равновесия переходный процесс при любых начальных условиях.

При k _л > k _гр такой переходный процесс возникает только при малых начальных условиях внутри неустойчивого предельного цикла. При больших начальных условиях амплитуда колебаний при переходном процессе стремится к значению a ₂, и в конечном итоге в системе устанавливаются автоколебания с этой амплитудой.