Упорядоченное множество

Множество, каждому элементу которого поставлено в соответствие некоторое число (немер этого элемента) от 1 до n, где n - число элементов множества, так что различным элементам соответствуют различные числа.

Имеется два существенно различных способа задания множеств. Можно либо перечислить все элементы множества, либо указать правило для определения того, принадлежит или не принадлежит рассматриваемому множеству любой данный объект. Таким образом, множество можно задать с помощью перечисления или с помощью описания.

При перечислении множества его элементы принято заключать в фигурные скобки: {2,4,6,…} — множество четных чисел,{3,6,9,…} — множество чисел кратных трем. Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.

С другой стороны, для задания (описания) некоторого множества X, состоящего из элементов, обладающих свойством a, используют запись X ={x|a(x)}. Читается как: «X — множество элементов x таких, что a(x) ". Например, Y={y|yͼN и y<7} — множество натуральных чисел, меньших 7.

Множество A равномощно множеству B, если существует биекция f:A→B.

Из того, что существует биекция f:A→B, следует, что соответствие f⁻¹ есть биекция B на A. Поэтому если A равномощно B, то и B равномощно A, и мы можем говорить, что множества A и B равномощны.

Факт равномощности множеств A и B будем записывать так: A∼B.

Из определения равномощности и свойств биекции также следует, что для любого множества A

имеет место A∼A (тождественное отображение есть биекция множества A на себя); а для любых множеств A,B,C из A∼B и B∼C следует A∼C (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть отношение эквивалентности, заданное на "множестве всех множеств" (на самом деле на множестве всех подмножеств некоторого универсального множества).

2.Подстановка.

Подстановкой (перестановкой) множества состоящего из первых натуральных чисел, называется взаимно-однозначное отображение множества на себя. Число в этом случае называется порядком подстановки.

Подстановки будем записывать в виде таблицы, состоящей из двух строк и столбцов следующим образом:

Пример. Примерами подстановок 5-го порядка будут подстановки:

Билет №3

1.Бинарные отношения и функции.

Отношение - это одна из форм всеобщей взаимосвязи всех предметов, явлений, процессов в природе, обществе и мышлении.

Обычно отношения обозначают латинской буквой R.

Если хRх для любого х из поля отношения R то такое отношение называют рефлексивным, где х и х - объекты мысли, а R - это знак о том или ином виде отношения между объектами мысли.

Если хRу → уRх, то такое отношение называется симметричным, где → - знак импликации, сходный с союзом "! если..., то..."

Если (xRy _^y R z)→ xRz, то такое отношение называется транзитивным, где _^ - знак конъюнкции.

Бинарное отношение, которое одновременно рефлексивно, симметрично и транзитивно называется отношением эквивалентности.

Бинарное отношение f называют функцией, если из <х, у> ͼ f и <х, z > ͼ f следует y = z. Бинарная функция применима к двум аргументам, взятым в определённом порядке, и только в этом случае она даёт значение функции для этих двух аргументов, взятых в данном порядке.

Бинарные функции называются тождественными, если они имеют одну и ту же область определения и если для каждой упорядоченной пары аргументов. лежащих в этой области, они имеют одно и тоже значение.

Бинарная функция называется симметричной, если она совпадает со своей конверсией, то есть когда меняются местами предыдущий и последующий члены высказывания.

Когда же f отображает Х на У и У ͼ Z то говорят, что f отображает Х в Z. Например, если f(x) = 2x для любого целого х, то можно сказать что f отображает множество всех целых чисел в множество всех целых чётных чисел.

2.Великие учёные, которые внесли вклад в развитие математической логики (не менее 5 перечислить; о двоих по выбору рассказать подробно.)

Бертран Рассел (1872 – 1970), А. Уайтхед (1861 – 1947), Д. Гильберт (1862 – 1943), К. Гёдель (1906 – 1978), А. Тарский (1901 – 1983).

Бе́ртран А́ртур Уи́льям Ра́ссел (18 мая 1872 — 2 февраля 1970) — британский философ, общественный деятель и математик. Рассел известен своими работами в защиту пацифизма, атеизма, а также либерализма и левых политических течений и внёс неоценимый вклад в математическую логику, историю философии и теорию познания. Менее известны его труды по эстетике, педагогике и социологии. Рассел считается одним из основателей английского неореализма, а также неопозитивизма.

В 1950 году получил Нобелевскую премию по литературе.

Андрее Эстерлинг, член Шведской академии, охарактеризовал учёного как «одного из самых блестящих представителей рационализма и гуманизма, бесстрашного борца за свободу слова и свободу мысли на Западе».

Американский философ Ирвин Эдман очень высоко ценил труды Рассела, даже сравнивал его с Вольтером, подчеркивая, что он, «как и его знаменитые соотечественники, философы старого времени, — мастер английской прозы».

В редакторских замечаниях к мемориальному сборнику «Бертран Рассел — философ века» (1967) отмечалось, что вклад Рассела в математическую логику является наиболее значительным и фундаментальным со времен Аристотеля.

Рассел считается одним из наиболее влиятельных логиков XX века.

Аристо́тель (384 до н. э., Стагира, Фракия — 322 до н. э., Халкида, остров Эвбея) — древнегреческий философ.

Математическая логика тесно связана с логикой и обязана ей своим возникновением. Основы логики, науки о законах и формах человеческого мышления (отсюда одно из ее названий формальная логика), были заложены величайшим древнегреческим философом Аристотелем (384—322 гг. до н. э.), который в своих трактатах обстоятельно исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления, в том числе законы противоречия и исключения третьего [1—5]. Вклад Аристотеля в логику весьма велик, недаром другое ее название — Аристотелева логика.

Еще сам Аристотель заметил, что между созданной им наукой и математикой (тогда она именовалась арифметикой) много общего. Он пытался соединить две эти науки, а именно свести размышление, или, вернее, умозаключение, к вычислению на основании исходных положений. В одном из своих трактатов Аристотель вплотную приблизился к одному из разделов математической логики — теории доказательств.

Билет №4

1.Данное высказывание записать в виде формулы логики высказываний: «Он хороший студент или хороший спортсмен»

A_˅B. Где А-«он хороший студент», а В-«он хороший спортсмен».

2.Метод математической индукции.

Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.

Метод математической индукции состоит в следующем:

Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:

1.P(1) является истинным предложением (утверждением);

2.P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).

Таким образом метод математической индукции предполагает два этапа:

1.Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).

2.Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).

Билет №5

1.Количество подмножеств Булевая. Теорема о булеане.

Теорема:

Число всех подмножеств множества из n элементов равно

Доказательство:

Перенумеруем элементы множества А и для каждого подмножества множества А построим последовательность длины n из нулей и единиц по следующему правилу: на k -ом месте пишем 1, если элемент с номером k входит в подмножество, и 0, если элемент с номером k не входит в подмножество.Итак, каждому подмножеству соответствует своя последовательность нулей и единиц.Например, пустому множеству соответствуем последовательность из одних нулей.Числовсех возможных последовательностей длины n, составленных из нулей иединиц, равно, согласно правилу умножения, 2*2*2*...*2 = .Следовательно, и число всех подмножеств множества А равно .

2.Бинарные отношения и их примеры.

СМ. Билет 3 Вопрос 1.

Примеры: Пусть X = {a, b, c, d}, Y = {1, 2, 3, 4, 5}. Тогда множество кортежей a={(a, 1), (b, 2), (c, 3), (d, 4)} являются соответствием из X в Y.

Билет №6

1.Операции над множествами. Свойства операций

Два множества А и В называются равными (А = В), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.

Говорят, что множество А содержится в множестве В (рис.1) или множество А является подмножеством множества В (в этом случае пишут А В),если каждый элемент множества А одновременно является элементом множества В. Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: 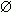А и А А.

Сумма (объединение) множеств А и В (пишется А В) есть множество элементов, каждый из которых принадлежит либо А, либо В. Таким образом, е А В тогда и только тогда, когда либо е А,либо е В.

Произведение (пересечение) множеств А и В (пишется А В, рис.2) есть множествоэлементов, каждый из которых принадлежит и А, и В. Таким образом, е А В тогда и только тогда, когда е А и е В.

Разность множеств А и В (пишется А – В, рис.3) есть множество элементов, которые принадлежат множеству А, но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В (пишется А \ В) есть множество:

А \ В = (А – В) (В – А).

Свойства операций над множествами:

2.Бинарные отношения, их виды и свойства. Связи с графами.

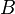Бинарное отношение в математике — двухместное отношение между любыми двумя множествами и , то есть всякое подмножество декартова произведения этих множеств: . Бинарное отношение на множестве — любое подмножество , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.

Виды бинарных отношений:

· Обратное отношение (отношение, обратное к ) — это двухместное отношение, состоящее из пар элементов , полученных перестановкой пар элементов данного отношения . Обозначается: . Для данного отношения и обратного ему верно равенство: .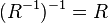

· Взаимо-обратные отношения (взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого.

· Рефлексивное отношение — двухместное отношение , определённое на некотором множестве и отличаю­щееся тем, что для любого этого множества элемент на­ходится в отношении к самому себе, то есть для любого элемента этого множества имеет место . Примеры рефлексивных отношений:равенство, одновременность, сходство.

· Антирефлексивное отношение (иррефлексивное отношение; так же, как антисимметричность не совпадает с несимметричностью, иррефлексивность не совпадает с нерефлексивностью) — бинарное отношение , определённое на некотором множестве и отличаю­щееся тем, что для любого элемента этого множества неверно, что оно находится в отношении к самому себе (неверно, что ), то есть возможен случай, что элемент множества не находится в отно­шении к самому себе.

· Транзитивное отношение — двухместное отношение , оп­ределённое на некотором множестве и отличающееся тем, что для любых из и следует (). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».

· Нетранзитивное отношение — двухместное отношение , оп­ределённое на некотором множестве и отличающееся тем, что для любых этого множества из и не следует (). Пример нетранзитивного отношения: «x отец y»

· Симметричное отношение — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любых элементов и этого множества из того, что находится к в отношении , следует, что и находится в том же отношении к — . Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.

· Антисимметричное отношение — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любых и из и следует (то есть и выполняются одновременно лишь для равных между собой членов).

· Асимметричное отношение — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любых и из следует . Пример: отношения «больше» (>) и «меньше» (<).

· Отношение эквивалентности — бинарное отношение между объектами и , являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.

· Отношение порядка — отношение, обладающие только некоторыми из трёх свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но несимметричное (например, «не больше») образует нестрогий порядок, а отношение транзитивное, но нерефлексивное и несимметричное (например, «меньше») — строгий порядок.

· Функция одного переменного — бинарное отношение , определённое на некотором мно­жестве, отличающееся тем, что каждому значению отно­шения соответствует лишь единственное значение . Свойство функциональности отно­шения записывается в виде аксиомы: .

· Биекция (взаимно-однозначное отношение) — бинарное отношение , определённое на некотором мно­жестве, отличающееся тем, что в нём каждому значению соответствует единственное значение , и каждому значению соответствует единственное значение .

· Связанное отношение — бинарное отношение , определённое на некотором множестве, отличающееся тем, что для любых двух различных элементов и из этого множества, одно из них находится в отношении к другому (то есть выполнено одно из двух соотношений: или ). Пример: отношение «меньше» (<).

Свойства отношений:

Бинарное отношение на некотором множестве может обладать различными свойствами, например:

· рефлексивность: ,

· антирефлексивность (иррефлексивность): ,

· корефлексивность: ,

· симметричность: ,

· антисимметричность: ,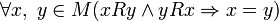

· асимметричность: , эквивалентна одновременной антирефлексивности и антисимметричности отношения,

· транзитивность: ,

· евклидовость: ,

· полнота (или связность^[2]): ,

· связность (или слабая связность^[2]): ,

· коннексность (англ. connex): ,

· трихотомия: верно ровно одно из трех утверждений: , или .

Наиболее удачным способ представить бинарные отношения R на множестве X – с помощью ориентированного графа, вершины которого представляют собой элементы множества X, а дуги – упорядоченные пары элементов, определяющие отношения R.

Билет №7

1.Операции двоичного сложения и ей свойства.

Сложение по модулю 2 (логическая неравнозначность, исключающее «ИЛИ», строгая дизъюнкция, XOR, поразрядное дополнение, побитовый комплемент, жегалкинское сложение) — булева функция, а также логическая и битовая операция. В случае двух переменных результат выполнения операции является истинным тогда и только тогда, когда лишь один из аргументов является истинным. Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных 1, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.

Сложение по модулю 2 следует отличать от простого сложения, которое соответствует обыкновенному не исключающему «или» (логической дизъюнкции).

В теории множеств сложению по модулю 2 соответствует операция разности двух множеств.

В префиксной записи

.

Свойства:

· (идемпотентность)

· (отрицание)

·

· (коммутативность)

· (ассоциативность)

·

· (сравнения по модулю)

2.Кванторы операции.

· Высказывание 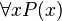означает, что область значений переменной включена в область истинности предиката .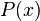

(«При всех значениях утверждение верно»).

· Высказывание означает, что область истинности предиката 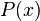непуста.

(«Существует , при котором утверждение верно»).