
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача № 4. Задача о назначениях
В общем виде задача о назначениях формулируется следующим образом:
Имеется n работ и n кандидатов для их выполнения. Затраты i – го кандидата на выполнение j – ой работы равны  . Каждый кандидат может быть назначен только на одну работу и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы при котором суммарные затраты на выполнение работы минимальны.
. Каждый кандидат может быть назначен только на одну работу и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы при котором суммарные затраты на выполнение работы минимальны.
Пусть x ij = 1 – значение переменной, если i – й кандидат
выполняет j – ю работу;
x ij = 0 – в противном случае.
Математическая постановка задачи
 - min (1)
- min (1)

 (2)
(2)
В целевую функцию (1) входят только те значения  для которых x ij
для которых x ij  , т.е. входят затраты соответствующие назначенным работам.
, т.е. входят затраты соответствующие назначенным работам.
Уравнения системы (2) означают, что каждый кандидат выполняет только одну работу и каждая работа может быть выполнена только одним кандидатом.
Решить задачу о назначениях – значит найти х ij удовлетворяющее (2) и доставляющее минимум (1).
Задача о назначениях является частным случаем транспортной задачи. Однако ее относительно простая структура позволяет разработать достаточно простые методы решения.
Одним из таких методов является венгерский метод.
Математическое обоснование венгерского метода решения задачи о назначениях заключено в трех теоремах.
Теорема Кененга
Если элементы матрицы разделить на два класса на основании свойства S, то минимальное число линий содержащих все элементы со свойствами S, равно максимальному числу таких элементов со свойством S, никакие два из которых не может на одной и той же линии. При решении задачи о назначениях венгерским методом свойство S состоит в том, что элемент матрицы нулевой.
Теорема А
Если набор X = (x ij) минимизирует функцию  по всем х ij, таким, что х ij
по всем х ij, таким, что х ij  и
и  , то Х = (x ij) минимизирует также функционал
, то Х = (x ij) минимизирует также функционал  , где
, где  , при всех
, при всех  ,
,  .
.
Другими словами говорят, что решение задачи о назначениях не изменится, если прибавить к любому столбцу или строке матрицы Сij некоторую константу или вычесть ее из них.
Теорема В
Если все Сij  и можно отыскать набор х = (x ij) такой, что
и можно отыскать набор х = (x ij) такой, что 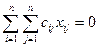 , то это решение оптимально.
, то это решение оптимально.
Алгоритм венгерского метода
Для решения задачи о назначениях составляют таблицу (табл. 2) в левой колонке записаны номера кандидатов, в верхней строке номера работ, а в i – ой строке и j – ом столбце стоят затраты на выполнение i – м кандидатом j – ой работы.
Таблица 2
| № | … | j | … | n | ||
| С11 | С12 | … | C1j | … | C1n | |
| С21 | С22 | … | C2j | … | C2n | |
| … | … | … | … | … | … | … |
| i | Ci1 | Ci2 | … | Cij | … | Cin |
| … | … | … | … | … | … | … |
| n | Cn1 | Cn2 | … | Cnj | … | Cnn |
Метод решения задачи сводится к прибавлению и вычитанию констант к строкам и столбцам (на основании теоремы А) до тех пор пока достаточное число величин Cij не образуется в ноль, что дает решение равное нулю (на основании теоремы В).
1 шаг. Получено в каждой строке, в каждом столбце. Для этого определяют сначала наименьший элемент в каждой строке и его значения отнимают от всех элементов этой строки. Затем в преобразованной таблице определяют минимальный элемент в каждом столбце и его значение вычитают из всех элементов этого столбца.
2 шаг. Если после выполнения 1-го шага алгоритма можно отметить нули в полученной таблице так, чтобы в каждой строке и в каждом столбце, находится один отмеченный нуль, то согласно теоремы, получим решение задачи.
Разметка нулей соответствует назначениям для них переменных x ij = 1. Другими словами, если назначение, которое получено, при всех отмеченных нулях, является полным (т.е. число отмеченных нулей равно n), то решение называется оптимальным.
В противном случае следует переходить к следующему шагу.
3 шаг. На основании теоремы Кенинга производят поиск. Набора строк, содержащих все нули. Доказано, что во всех матрицах n х n все нули можно пересечь меньшим числом линий чем n, тогда и только тогда, когда эти нули не обеспечивает решение задачи. Для этого пользуются следующими правилами:
а) отмечают все строки, в которых не имеется ни одного отмеченного нуля;
б) отмечают все столбцы, содержащие неотмеченный нуль хотя бы в одной из отмеченных строк;
в) отмечают все стороны, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов.
Действия (б) и (в) повторяют поочередно до тех пор, пока существуют варианты для разметки. После этого вычерчивают отмеченные столбцы и неотмеченные строки.
Цель третьего шага – провести минимальное число горизонтальных и вертикальных линий, пересекающих, по крайней мере, один раз все нули.
4 шаг. Перестановка некоторых нулей. Находят наименьшее число из тех, которые остались не вычеркнутыми после третьего шага. Затем вычитают это число из не вычеркнутых столбцов (точнее и тех столбцов, которые содержат не вычеркнутые элементы) и прибавляют это число по всем вычеркнутым строкам.
Это шаг не изменяет оптимального решения и после его выполнения появится, по крайней мере, один новый ноль. Далее следует вернуться к шагу 2 и весь цикл расчета повторять до тех пор, пока не будет получено оптимальное решение.
Задача Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты первого проекта являются входными данными для второго проекта, выходные результата второго проекта – это входные данные для третьего проекта, результаты третьего проекта используются для работы над четвертым проектом.
В качестве научных руководителей проектов кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время необходимое ему для реализации проекта. Матрица времен задана.

В i – ой строке и j – ом столбце матрицы Т стоит время на выполнение i – м ученым j – го проекта.
Пусть продолжительность времени задана в месяцах и требуется выбрать научного руководителя для выполнения каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным.
Решение:
В данной задаче о назначениях в качестве работ рассматриваются исследовательские проекты, а в качестве кандидатов – ученые, претендующие на роль научных руководителей.
Введем переменные х ij. х ij = 1 – если j – й ученый научный руководитель j – го проекта.
х ij = 0 – если i – й ученые не являются руководителем j – го проекта.
Целевая функция задачи в общем виде:
С = 3 х 11 + 7 х 12 + 5 х 13 + 8 х 14 + 2 х 21 + 4 х 22 + 4 х 23 + 5 х 24 + 4 х 31 + 7 х 32 + 2 х 33 + 8 х 34 + 9 х 41 + 7 х 42 + 3 х 43 + 8 х 44 → min.
Составляем таблицу 3
| № | |||||
Вычитаем минимальные элементы из каждой строки и записываем в таблицу 4.
Таблица 4
| № | ||||
Вычитаем минимальные элементы из соответствующих столбцов и запишем таблицу в 5.
Таблица 5
| № |  3 3
| |||
 1 1
| 0. | |||
 2 2
| 0. | |||
| 0. | ||||
В таблице 5 вычеркивание произведем таким образом, чтобы в каждой строке и в каждом столбце отмеченными оказались по одному нулю.
- Отметим точкой О в первой строке и в первом столбце. Другой О первого столбца остается неотмеченным. Это означает, что если первый ученый назначен научным руководителем первого проекта, второй ученый уже не может быть назначен на этот же проект.
- Отмечаем О стоящий во второй строке и втором столбце и оставляем неотмеченным О стоящий в четвертом столбце, т.к. второй ученый уже назначен руководителем второго проекта.
- Отмечаем О третьей строки и третьего столбца и оставляем неотмеченным О в четвертой строке, поскольку четвертый ученый уже не может быть назначен для руководства третьим проектом.
Число отмеченных нулей 3, т.е. назначение не полное. Переходим к шагу 3 алгоритма. Найдем минимальный набор строк и столбцов, содержащих все нули.
В рассматриваемой задаче следует вычеркнуть первую и вторую строки и третий столбец.
Зачеркнутые строки и столбцы тем минимальным набором, который содержит все нули.
Переходим к четвертому шагу алгоритма венгерского метода. В оставшихся не вычеркнутыми клетках минимальный элемент равен 2.
Вычитаем его из каждого элемента не вычеркнутых (1, 2, 4) столбцов. Получим таблицу 6.
Таблица 6
| № | ||||
| -2 | ||||
| -2 | -2 | -2 | ||
Прибавим 2 к каждому элементу вычеркнутых строк и получим преобразованную таблицу 7.
Таблица 7
| № | ||||
| 0. | ||||
| 0. | ||||
| 0. | ||||
| 0. |
Возвращаемся к шагу 2, и вновь сделаем назначения, отметив по порядку нуля в таблице. В этот раз назначение полное, т.к. число отмеченных нулей – 4.
В итоге получим следующее назначение: Х* = (х 11, х 22, х 33, х 44), т.е.
- х 11 = 1 – первый ученый назначается руководителем первого проекта;
- х 22 = 1 – второй ученый руководитель второго проекта;
- х 33 = 1 – третий ученый руководитель третьего проекта;
- х 44 = 1 – четвертый ученый руководитель четвертого проекта.
Целевая функция – время выполнения всего проекта
 ,
, 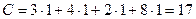 дней.
дней.
В рассматриваемой задаче данное назначение не является единственным. Существует еще одно назначение, приведенное в таблице 8.
Таблица 8
| № | ||||
| 0. | ||||
| 0. | ||||
| 0. | ||||
| 0. |
Х 2 * = (х 11, х 24, х 33, х 42)
В этом варианте назначения осуществлены следующим образом:
- х 11 = 1 – первый ученый руководит первым проектом;
- х 24 = 1 – второй ученый руководит четвертым проектом;
- х 33 = 1 – третий ученый назначен на третий проект;
- х 42 = 1 – четвертый ученый руководит вторым проектом.
Целевая функция, время выполнения проектов
 дней - не меняется.
дней - не меняется.
Вывод: Получены два оптимальных назначения, которым соответствует минимальное время осуществления проекта четырьмя учеными.
Определение. Говорят, что i -я операция доминирует j -ю, если:

Или:

Определение Операция называется оптимальной по Парето, если не существует операций, которые бы ее доминировали.
Задача № 6
Инвестор рассматривает четыре инвестиционные операции со случайными эффективностями, описываемыми случайными величинами Y 1, Y 2, Y 3, Y 4 с рядами распределения:
| Y 1 | Y 2 | ||||||||
| p | 1/6 | 1/2 | 1/6 | 1/6 | p | 1/2 | 1/6 | 1/6 | 1/6 |
| Y 3 | Y 4 | ||||||||
| p | 1/6 | 1/6 | 1/6 | 1/2 | p | 1/3 | 1/3 | 1/6 | 1/6 |
Необходимо определить, какие из этих операций оптимальны по Парето.
Решение:
Ожидаемые эффективности и риски равны соответственно:
M (Y 1) = 5,00, M (Y 2) = 4,33, M (Y 3) = 7,50, M (Y 4) = 3,67; σ(Y 1) = 0,58, σ(Y 2) = 3,59, σ(Y 3) = 2,93; σ(Y4) = 2,05.
Нанесем точки ( ) на единый график (рис. 5). i -я операция доминирует j -ю, если точка, соответствующая i -й операции, находится на графике правее и ниже точки, соответствующей j -й операции.
) на единый график (рис. 5). i -я операция доминирует j -ю, если точка, соответствующая i -й операции, находится на графике правее и ниже точки, соответствующей j -й операции.

Рис. 5.
Видно, что первая операция доминирует вторую и четвертую, третья операция доминирует вторую. При этом первая операция не доминирует третью, а третья не доминирует первую. Первая и третья операции, таким образом, оптимальны по Парето.
Задача № 7
Группа из 5 экспертов оценивает качество изделий, изготовленных на 7 предприятиях. Их предпочтения представлены в таблице. Вычислить коэффициент конкордации рангов Кендалла и оценить его значимость на уровне α = 0,05.
Решение.
Коэффициент конкордации рангов рассчитывается по формуле:
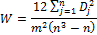
где n – число альтернатив, m – число экспертов.

| Предприятие | |||||||
| Эксперт | |||||||

| |||||||

| -12 | -10 | -5 | ||||

|
В итоговой строке таблицы приведены суммы рангов изделий по каждому из 7 предприятий, полученных от 5 экспертов. Средняя сумма рангов равна 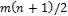 = 5(7+1)/2=20.
= 5(7+1)/2=20.  .
.
Вычислим коэффициент конкордации:

Данное значение свидетельствует о достаточно сильно степени согласованности мнений экспертов. Оценим статистическую значимость коэффициента конкордации рангов с помощью  критерия на уровне 0,05.
критерия на уровне 0,05.
Проверяется нулевая гипотеза об отсутствии корреляции рангов ( ). Конкурирующая гипотеза –
). Конкурирующая гипотеза – 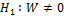 .
.
Найдем наблюдаемое значение  критерия:
критерия:

Найдем табличное значение  критерия в приложении 2:
критерия в приложении 2:


Поскольку наблюдаемое значение  критерия превышает табличное, то нулевая гипотеза отклоняется на уровне значимости 0,05, т.е. признается статистическая значимость коэффициента конкордации рангов.
критерия превышает табличное, то нулевая гипотеза отклоняется на уровне значимости 0,05, т.е. признается статистическая значимость коэффициента конкордации рангов.
Date: 2016-05-14; view: 1532; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |