Тригонометрические функции. Из равенства (2.2) вытекает знаменитая формула Эйлера

для вещественных .

Далее

.

Из двух последних равенств следует, что

, . (2.6)

Поэтому естественно положить

, . (2.7)

Так определенные функции будут заданы при всех комплексных и при вещественных 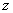(то есть при ) будут, в силу (2.6), совпадать с и 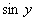соответственно.

Из (2.7) непосредственными вычислениями можно показать, что все формулы сложения, формулы приведения для тригонометрических функций переносятся с вещественной на комплексную переменные. Для иллюстрации проверим знаменитое равенство

.

В самом деле

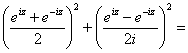
В вещественном анализе из этого тождества делается вывод о том, что синус и косинус – ограниченные функции. В случае комплексных переменных это не так. Более того, оказывается, что на комплексной плоскости эти две функции принимают все комплексные значения. То есть уравнения

,

имеют решения при любых .

Рассмотрим для краткости только случай косинуса

.

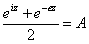Тогда

и .

Положим , тогда

,

и поэтому

.

(Заметим, что теперь корень можно извлечь из любого комплексного числа.) Значит

,

поэтому

,

если . Из формул Виета следует, произведение корней и равно единице (свободному члену в квадратном уравнении), поэтому ни , ни неравны нулю. Следовательно, решение

существует при любом .

В частности, решение уравнения естественно назвать . Таким образом получим, что

.

Аналогично можно показать, что

.

Уравнение имеет решение

,

то есть обращается в нуль в тех же точках, что косинус вещественного переменного. Иными словами расширение области определения не добавило нулей этой функции. То же самое относится и к функции . Она обращается в нуль в точках , где .

Функции в силу вышесказанного определена при всех, где .

Аналогично определена при , где

Date: 2016-01-20; view: 524; Нарушение авторских прав