
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дробный факторный эксперимент
Как указывалось выше, план ПФЭ содержит 2k опытов. С ростом числа факторов k объем необходимого эксперимента быстро возрастает и становится трудновыполнимым и дорогим. Перед экспериментатором возникает задача сокращения числа опытов, рассматривая прежнее число факторов k. Теория планирования эксперимента дает правила сокращения опытов, гарантируя минимальную потерю информации. Один из способов - дробный факторный эксперимент (ДФЭ), основанный на том, что во многих случаях наиболее важная информация содержится в линейных членах уравнения регрессии - коэффициентах влияния факторов. Взаимодействия часто малы или дают второстепенные сведения.
Число опытов в ПФЭ превышает число коэффициентов регрессии линейной модели (bi¹0; bij=0), причем тем больше, чем больше факторов. Поэтому число опытов для решения задачи интерполяции с построением модели только с членами biхi. можно сократить, применяя ДФЭ.
Дробным факторным экспериментом называется такой эксперимент, который содержит часть точек ПФЭ.
Покажем на примере, как получить план ДФЭ из простейшего ПФЭ 22. В ПФЭ 22 (см. табл. 3.4) можно вычислить четыре не смешанных (не зависящих друг от друга - вспомним свойство ортогональности) между собой коэффициента и представить результаты эксперимента полиномом первого порядка у=b0+b1x1+b2x2+b12x1х2. Если в выбранных интервалах варьирования достаточно для адекватного описания первых трех членов, то необходимо определить три коэффициента b0, b1 и b2. Так как при этом b12→0, то вектор-столбец x1х2 можно использовать для введения в планирование нового фактора х3. В этом случае в первом и четвертом опытах он должен быть на верхнем уровне, а во втором и третьем - на нижнем.
Таким образом, достаточно выполнить всего четыре опыта для оценки влияния трех факторов, т.е. воспользоваться половиной полного факторного эксперимента 23, или, как принято называть в планировании эксперимента, «полурепликой» 23-1 (табл. 3.6), и, следовательно, можно представить результаты эксперимента по этой полуреплике уравнением у=b0+b1x1+b2x2+b3x3.
Причем коэффициенты bi. вычисляются по общей формуле (3.10) и полученное уравнение обладает свойством ортогональности, т.е. все коэффициенты bi найдены независимо друг от друга.
Заметим, что коэффициент b3 в данном уравнении вычисляется по такому же выражению, как вычислялся бы и коэффициент взаимодействия b12 (значения у суммируются со знаками последнего столбца матрицы). Это означает, что найденный коэффициент b3 отражает и не учитываемое в уравнении взаимодействие факторов x1х2, т.е. имеет место смешивание эффектов. Можно показать, что из-за сокращения (вдвое) числа опытов по сравнению с ПФЭ смешанными со взаимодействиями оказываются и два других линейных члена, а именно b1 с b23 и b2 с b13. Однако для ДФЭ такое смешивание малосущественно, так как постулируется незначительность взаимодействий.
Таблица 3.6
| Номер опыта | zi | yu | |||
| x0 | x1 | x2 | x3ºx1x2 | ||
| + | - | - | + | y1 | |
| + | + | - | - | y2 | |
| + | - | + | - | y3 | |
| + | + | + | + | y4 |
Итак, дробный факторный эксперимент применяется для локального описания линейными моделями поверхности отклика таких объектов, математическое описание которых не может иметь (или имеет пренебрежимо малые, незначимые) хотя бы некоторые из взаимодействий. При построении дробных реплик пользуются универсальным правилом (смешивания линейных эффектов и взаимодействий): при введении в планирование нового фактора следует поместить его в вектор-столбец, принадлежащий высшему взаимодействию, которым можно пренебречь.
Дробная реплика (часть ПФЭ), в которой р линейных эффектов приравнены к эффектам взаимодействия, обозначается так: 2k-p.
На практике широко применяются планы ДФЭ, основанные на использовании матрицы ПФЭ 23 (см. табл. 3.5), состоящей из восьми опытов. Заменив столбец x1x2x3 новым фактором x4, получим полуреплику 24-1 - сокращенный вдвое план четырехфакторного ПФЭ. Далее, заменив пятым фактором столбец x1x2, получим четверть-реплику 25-2 - плана ДФЭ для пяти факторов. Действуя так же, можно ввести вместо оставшихся взаимодействий еще два фактора и получить насыщенный план, согласно которому, проведя всего восемь опытов, можно изучить влияние семи факторов, определить восемь коэффициентов регрессии и составить уравнение вида у=b0+b1x1+b2x2+b3x3+b4x4+b5x5+b6x6+b7x7.
Все коэффициенты bi независимы, однако полностью утеряны сведения о взаимодействиях.
Можно убедиться, обратившись к рис. 3.4, что ДФЭ действительно практический способ минимизации опытов без потерь существенной информации. ПФЭ 23 - это куб, вершины которого обозначены кружками и зачерненными точками. Чтобы вместо восьми опытов выполнить четыре, оптимально использовав факторное пространство, следует провести опыты, обозначенные либо только кружками, либо только зачерненными точками, а и те, и другие являются полурепликами ПФЭ 23. Любые другие варианты несимметричны относительно центра плана и не могут гарантировать от значительных потерь информации.
С увеличением числа факторов выбор реплик усложняется, так как быстро увеличивается число реплик различной дробности. Выбор дробной реплики требует предварительного тщательного анализа. Применяя дробное планирование, необходимо точно знать систему смешивания и четко представлять цену потерянной информации.
Дробное факторное планирование на практике применяется при исследовании ГТД и его узлов, если число факторов более трех-пяти. В работе [2] приведен пример ДФЭ.
Планирование эксперимента для получения полинома второй степени
Если из имеющейся априорной информации известно, что изучаемая характеристика объекта явно нелинейна и не может быть описана полиномом первого порядка, то возникает задача о составлении рационального плана экспериментов, позволяющего получить уравнение регрессии в виде полинома второго порядка. Неадекватность модели в виде полинома первого порядка, установленная проверкой по F-критерию, также свидетельствует о необходимости описания полиномом более высокой степени. Об этом же можно судить по разности |y0-b0|, которая статистически значима при существенных квадратичных членах.
В теории планирования эксперимента разработано много различных планов второго порядка, отличающихся числом опытов, расположением точек в факторном пространстве, свойствами получаемого уравнения регрессии. Остановимся на композиционных планах, которые образуются дополнением планов первого порядка.
Если добавить к плану для оценки коэффициентов полинома первого порядка (в планировании он называется ядром плана второго порядка) еще несколько опытов в точках, специальным образом расположенных относительно ядра (они называются «звездные» точки) и в центре плана, то можно определить на основе полученного таким образом плана коэффициенты полинома второго порядка.
На примере трех факторов поясним алгоритм построения композиционного плана второго порядка (рис. 3.4). Сначала планируются опыты по плану первого порядка (ПФЭ типа 23) в точках, обозначенных светлыми и зачерненными кружками, и опыты в центре плана.
И, как сказано выше, планируют еще шесть опытов в «звездных» точках (на рис. 3.4 обозначены *) с координатами (±а, 0, 0), (0, ±а, 0), (0, 0, ±а), расположенных на осях. «Звездные» точки расширяют область эксперимента и дают возможность определить коэффициенты полиномиальной модели второй степени, если правильно выбрать расстояние а до «звездных» точек. Общее число опытов при реализации композиционного плана второго порядка составляет Nk=2k+2k+n0, где n0 - число повторных опытов в центре

Рис. 3.4. План трехфакторного эксперимента для получения полинома второго порядка
плана. Для ядра композиционного плана второго порядка можно использовать и ДФЭ (на рис. 3.4 или только зачерненные кружки, или - незачерненные). Расстояние а до звездных точек выбирают из условия использования какого-либо критерия оптимальности плана эксперимента. Такими критериями могут быть рассмотренные выше ортогональность или ротатабельность плана.
Расчет коэффициентов регрессии и статистический анализ полученного уравнения регрессии проводят на ЭВМ с помощью пакета прикладных программ.
Для построения модели второй степени ротатабельный и ортогональный планы равнозначны. Следует заметить, что ни ортогональные, ни ротатабельные композиционные планы не являются оптимальными, поскольку при таком планировании нарушается принцип максимального использования факторного пространства. Это видно на рис. 3.4, где при построении плана не используются углы куба (±a, ±а, ±а), т.е. используется не все факторное пространство, отведенное для эксперимента. Поэтому разработаны и другие критерии оптимальности для планов второго порядка, лишенных указанного недостатка.
Как при решении задачи интерполяции, так и особенно при решении задачи оптимизации полученный полином второго порядка
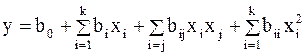 (3.18)
(3.18)
необходимо подвергнуть анализу.
Можно с помощью адекватного полинома второй степени предсказать точку экстремума. Для этого необходимо решить систему линейных уравнений, получаемых из условий экстремума уравнения регрессии:

 (3.19)
(3.19)

При решении системы линейных уравнений (3.19) следует иметь в виду, что координаты экстремальной (оптимальной) точки х. получены в закодированных (относительных) единицах, а начало координат находится в центре эксперимента. Подставляя в уравнение (3.18) координаты xic,, можно предсказать оптимальное значение функции отклика уc.
Анализ нелинейной модели не заканчивается определением экстремальной точки, а в общем случае включает изучение поверхности отклика. Поверхности второго порядка удобно анализировать после преобразования полинома вида (3.18) к каноническому виду.
Date: 2016-01-20; view: 1294; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |