Определение оценок случайных погрешностей

В основе практического определения характеристик случайных погрешностей измерений лежит проведение повторных наблюдений измеряемой величины. В случае градуировки средств измерений значение измеряемой величины заведомо известно (например, оно воспроизводится образцовой мерой) и полученные данные будут характеризовать точность используемых средств измерений (измерительного прибора, измерительного канала и т.д.).

При повторных наблюдениях какого-либо параметра в реальных условиях на получаемые результаты будут влиять не только погрешности средств измерений, но и особенности функционирования экспериментального объекта и его элементов (точность поддержания режима; стабильность рабочего процесса; точность изготовления и сборки, если используются различные экземпляры объекта и т.д.). Поэтому полученные характеристики погрешностей будут в целом отражать точность воспроизведения результатов эксперимента с принятой системой измерений в данных конкретных условиях.

Результаты повторных наблюдений служат также основой для выяснения многих других вопросов, возникающих при проведении испытаний', таких, например, как определение эффективности мероприятий при доводке, сравнение по точности различных способов измерений и т.д.

Характеристики случайных величин могут быть строго определены только тогда, когда известна генеральная совокупность значений случайной величины - достаточно большое (теоретически бесконечное) множество всех мыслимых значений случайной величины. Однако на практике имеется лишь некоторое конечное, обычно небольшое, число n результатов наблюдения (х₁, х₂,..., х_n) - конечная выборка объема n. Возникает задача оценивания параметров генеральной совокупности (в первую очередь, математического ожидания и дисперсии) случайных величин по выборочным данным. Оценка называется точечной, если она выражается одним числом.

Для того чтобы оценка была пригодной для описания оцениваемых параметров, она должна удовлетворять следующим требованиям:

- несмещенности - ее математическое ожидание должно быть равно оцениваемому параметру;

- эффективности - ее дисперсия должна быть минимальной по сравнению с другими оценками;

- состоятельности - с ростом объема выборки она должна приближаться к значению оцениваемого параметра.

Можно доказать, что с учетом перечисленных требований наилучшей выборочной оценкой математического ожидания является выборочное среднее значение

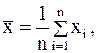
а оценкой дисперсии - исправленная выборочная дисперсия

Применив правила вычисления дисперсии суммы случайных величин и произведения случайной величины на постоянный множитель, получим S²()=S²(x)/n, т.е. дисперсия выборочной средней в n раз меньше дисперсии отдельного наблюдения. Соответственно среднее квадратическое отклонение S() уменьшается в раз.

Таким образом, увеличение объема выборки я равносильно повышению точности измерений. Поэтому при проведении повторных наблюдений за результат измерения принимается значение .

Для определения по заданной доверительной вероятности доверительного интервала для результата измерения необходимо образовать нормированную случайную величину t=( -a)/S()=( -а) /S(x). В том случае, когда известна дисперсия генеральной совокупности (S(x)=s(х)), то t=z и доверительный интервал может быть найден с использованием стандартной функции Ф(z) для нормированного нормального распределения (см. разд. 2.2). Если же значение S(x) определяется по выборке, то величина t подчиняется не нормальному распределению, а так называемому распределению Стьюдента. В отличие от нормального распределения оно зависит от объема выборки n или, точнее, от числа степеней свободы f=n-1. С ростом n, когда величина S²(х) все точнее определяет генеральную дисперсию, распределение Стьюдента приближается к нормальному.

Для распределения Стьюдента составлены таблицы, позволяющие находить критические значения t=t_g.f, при выбранной доверительной вероятности у и числе степеней свободы f=n-1, а также доверительную границу случайной погрешности D()=| -а|=t_g.fS()=t_g.fS(x)/ .

На рис. 2.2 приведены кривые зависимостей g=f(t_g), соответствующие различным значениям t. Как видно, при малых значениях f и равной вероятности для распределения Стьюдента возможны большие отклонения от среднего значения по сравнению с нормальным распределением, так как в этом случае сама дисперсия определена с некоторой неопределенностью.

Пример. Пусть по выборке объемом n=4 вычислено значение =50, являющееся результатом измерения некоторой величины а, причем известно, что дисперсия генеральной совокупности s²[х]=4 или s(х)=2. Необходимо определить доверительный интервал при значении доверительной вероятности g=0,95. Так как в атом случае g=2Ф(z_g), то находим, что значению Ф(z_g)= g/2=0,475 соответствует критическое значение z_g=1,96. Это означает, что с вероятностью 0,95 случайная величина z находится в пределах -1,96<z£1,96, или доверительная граница случайной погрешности D()=| -а|=z_gs()=z_gs(x)/ =1,96^.2/ »2 (значение погрешности округляется до второй значащей цифры).

Найдем доверительный интервал для тех же исходных данных, но предположим, что по экспериментальным данным определена также выборочная дисперсия S²(х)=4. Для g=0,95 и f=4-1=3 находим t_g.f=3,18.

Это означает, что рассматриваемая величина t лежит в пределах -3,18<t<+3,18 или D()=t_g.fS()/ =3,2.

Таким образом, во втором случае доверительный интервал шире, чем в первом. Это следствие возможной неточности в определении дисперсии по малому числу измерений.

Для получения объективных данных при обработке результатов повторных наблюдений необходимо исключить результаты, искаженные грубыми погрешностями. В первую очередь должны быть проверены те результаты наблюдений х_k, которые наиболее сильно отличаются от средней арифметической величины . Для этого вычисляется параметр и сравнивается с табличным значением n_кр для принятого уровня значимости q=1-g. Если n>n_кр, то данный результат следует отбросить и вновь определить и S(x) по оставшимся данным.

При косвенных измерениях также возникает задача оценивания истинного значения измеряемой величины g и ее погрешностей. Пусть величина g связана с параметрами x_i, измеряемыми прямыми методами, уравнением g=F(x₁, x₂,...; x_n). Доказано, что в случае выполнения повторных наблюдений для получения наилучшей оценки истинного значения величины g (т.е. для того, чтобы величина g обладала наименьшей дисперсией) в исходное уравнение должны быть подставлены средние арифметические значения параметров , ,..., .

Если погрешности параметров x_i не коррелированы, т.е. отсутствует взаимосвязь между ними (это в большинстве случаев имеет место на практике), то формула для определения средней квадратической погрешности будет иметь вид

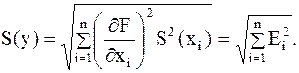(2.1)

Величины называются частными погрешностями результата косвенного измерения.

При вычислении погрешностей результат округляется до двух значащих цифр и небольшие частные погрешности могут на него вообще не оказывать влияния. Частной погрешностью E_k можно пренебречь, если выполняется неравенство E_k<0,3S(y). Это неравенство называется критерием ничтожности погрешностей, а отвечающие ему погрешности - ничтожными.

Доверительный интервал для результата косвенного измерения определяется с помощью рассмотренного выше распределения Стьюдента. Эффективное число степеней свободы при этом должно быть найдено по формуле

Здесь m_i - число повторных наблюдений величин x_i.

В практических расчетах чаще применяются относительные величины погрешностей ; . Чтобы перейти к ним, необходимо обе части выражения (2.1) разделить на у, а каждое слагаемое в подкоренной сумме умножить и разделить на :

;

.

Величины представляют собой относительные коэффициенты влияния погрешности на .

Если функция у=F(x₁, x₂,..., x_n) логарифмируема, то для удобства вычислений величины К. целесообразно представить в виде .

Пример. Расход газа в мерном участке экспериментальной установки вычисляется по формуле

.

Здесь m - коэффициент расхода, учитывающий неравномерность поля скоростей; D - диаметр участка; r - плотность газа; Dр=р*-р - динамический напор в центре сечения. Известны относительные значения средних квадратических погрешностей, полученных в результате трехкратных наблюдений: ; ; . Значение диаметра D определено с точностью d_D=±0,4% (предельные отклонения). Принимая, что закон распределения d_D равномерный, получим .

Требуется определить доверительный интервал для величины G при доверительной вероятности g=0,95. Для этого прологарифмируем выражение для G:

.

Найдем коэффициенты влияния К_D,G=D^.2¶(lnD)/ ¶D=2; аналогично найдем К_m,G=1; К_r,G=К_Dp,G=0,5.

Частные относительные погрешности исходных величин

E_i=K_i,G^.S_i; ; ;

; .

Среднее квадратическое отклонение

.

Поскольку значения и меньше 0,3 , то эти частные погрешности будут ничтожно малыми, т.е. повышение точности измерений величин р и Dр не приведет в данном случае к заметному повышению точности измерения расхода G.

Эффективное число степеней свободы f_эф=25; значение t_0,95;25»2,0. Отсюда доверительная граница относительной случайной погрешности при g=0,95.

Date: 2016-01-20; view: 745; Нарушение авторских прав