І. Задачі, які приводять до диференціальних рів­нянь

План

Вступ

Розділ І. Задачі, які приводять до диференціальних рів­нянь.

Розділ ІІ. Диференційні рівняння в прикладних задачах

2.1. Методика складання диференціальних рівнянь

2.2. Схема складання диференціального рівняння

Розділ ІІІ. Прикладні задачі

Висновки

Список використаної літератури

Вступ

Під час розв'язування багатьох практичних задач дово­диться знаходити невідому функцію з рівняння, яке міс­тить поряд з цією невідомою функцією її похідні.

Рівняння, яке містить невідому функцію та її похідні, називається диференціальним. Порядок найвищої похід­ної, яка входить до диференціального рівняння, назива­ється його порядком. Наприклад, рівняння

y ''+ 4у = 0 є диференціальним рівнянням другого порядку.

Якщо до рівняння входить незалежна змінна, невідома функція і її похідна, то це рівняння називається диферен­ціальним рівнянням першого порядку. Якщо, крім того, в рівняння входить похідна другого порядку від шуканої функції, то рівняння називається диференціальним рів­нянням другого порядку і т. д.

В даній роботі буде розглянуто прикладні задачі, які зводяться до розв’язання диференціальних рівнянь, а також розглянута методика та схема розв’язання диференціальних рівнянь.

І. Задачі, які приводять до диференціальних рів­нянь.

Використання математичних моделей є одним з найбільш ефективних методів вивчення різноманітних фізичних процесів і явищ. Математичні моделі допомагають зрозуміти фізичний процес, дають можливість установити якісні та кількісні харак­теристики його стану, з їх використанням можна передбачити подальший розвиток процесу без натуральних експериментів, проведення яких у багатьох випадках є надто дорогим або просто неможливим.

Вивчаючи фізичні явища, не завжди вдається безпосередньо знайти закони або формули, які пов’язують між собою величи­ни фізичного процесу, але часто можна виявити певну функціо­нальну залежність між невідомими характеристиками процесу, швидкостями їх зміни й часом, тобто знайти рівняння, які мі­стять похідні невідомих характеристик процесу.

Розв’язування задачі дослідження певного фізичного явища чи процесу можна розділити на два етапи:

1. Складання диференціального рівняння, яке при певних припущеннях описує сутність явища чи процесу.

2. Знаходження розв’язку диференціального рівняння, тобто функціональної залежності між величинами, які характеризу­ють фізичне явище.

Для складання диференціальних рівнянь природничих наук використовують фізичний зміст першої та другої похідних, а та­кож додаткові умови та закони, притаманні конкретній галузі науки, такі як-от:

- другий закон Ньютона (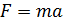, де т – маса тіла, а – прискорення руху, – сума сил, що діють на тіло);

- закон всесвітнього тяжіння (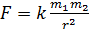, де – маси двох тіл, r – відстань між ними);

- закон Кірхгофа (алгебрична сума сил струмів, які протіка­ють у певній точці електричного кола, дорівнює нулю);

- закон Фур’є (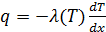, де – питомий потік теплоти,

– коефіцієнт теплопровідності середовища, – швидкість зміни температури Т);

- закон Ньютона про охолодження тіла (швидкість охолодже­ння тіла пропорційна різниці температур тіла та середовища);

- закон розчинення речовини (швидкість розчинення пропор­ційна наявній кількості нерозчиненої речовини та різниці концен­трацій насиченого розчину і розчину у певний момент часу);

- закон Гука (сила пружності пружини пропорційна її видов­женню) тощо.

Питання про відповідність математичної моделі й реального явища вивчається на основі аналізу результатів досліду та їх по­рівняння з поведінкою розв’язку одержаного диференціального рівняння.

Зауважимо, що багато розділів фізики значною мірою мож­на розглядати як різні розділи теорії диференціальних рівнянь. Перш за все це виявляється в аналітичній механіці, яку бага­то вчених розглядають як математичну дисципліну. Основним апаратом сучасної теоретичної фізики також є диференціальні рівняння.

Розглянемо деякі прикладні задачі, які приводить до ди­ференціальних рівнянь.

Задача 1. Матеріальна точка Р рухається по прямій, яку приймемо за вісь x, і в момент часу t займає положення х (рис. 1.1). Відома швидкість руху v(t). Знайти закон руху точки, тобто залежність х від t, якщо відомо, що у момент часу точка Р займає положення .

Рис. 1.1

Розв’язання. З курсу математичного аналізу відомо, що швид­кість точки у момент часу t дорівнює похідній х'(t) (фізичний зміст похідної), тобто

х'(і)= v(t). (1.1)

Співвідношення (1.1) є диференціальним рівнянням руху точки Р і задає закон її руху в диференціальній формі. Інтегруючи рівняння (1.1), одержуємо:

де C — довільна стала (стала інтегрування).

За умовою задачі, x(t₀) = x₀. Підставляючи в (1.2) x = x₀ і t = 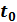, одержуємо, що C =x₀. Отже, шуканим розв’язком (рухом) є

Розглянемо задачу геометричного змісту. Розв‘язання цієї задачі допоможе з‘ясувати зміст довільних сталих.

Задача 2. Знайти рівняння кривої, що проходить через точку М (1;2), якщо кутовий коефіцієнт проведеної до нього дотичної дорівнює 4x­­­_­­­­­­­_­­³.

Розв‘язання. У цій задачі треба знайти формулу, що задає функцію F, похідною якої є функція f (x) = 4x³ , тобто треба знайти первісну функції y=4x³. Крім того, відомо, що графік шуканої функції проходить через задану точку М (1;2).

Множина первісних всіх функцій для функції y=4x³ має вигляд F(x) = x⁴+С, де С – довільна стала. Щоб виділити з цієї множини первісну, графік якої проходить через точку М (1;2), враховується, що коли x=1, значення функції F (1) має дорівнювати 2. Підставляючи у рівність F(x) = x⁴+С замість x число1, а замість F(x) – число 2, дістанемо 2 = 1 + С, звідки С=1. Підставляючи значення С в ту саму рівність дістанемо, що F(x) = x⁴+1 – шукане рівняння кривої, яка проходить через точку М (1;2).