Полиномы над полем Q

f(x)=a₀xⁿ+…a_nÎQ[x]. для исслед-я многочл над полем Q м. полагать что коэф многочл f(x) целые числа. Если коэф дробные, то f(x) умножаем на общ знамен чисел a₀,…,a_n при этом корни многочл не измен-ся и на разлож на множ-ли f(x) это тоже не повлияет 1) целые корни f(x)=a₀xⁿ+…a_nÎZ[x] Для нахожд целых корней исп след Т. Т₁: целые корни мног f(x) явл-ся делителями своб члена a_n. Док-во: пусть aÎZ, a-корень f(x), тогда f(a)=a₀aⁿ+…+a_n-1a+a_n=0, => a_n=-a (a₀a^n-1+…+a_n-1) => a_n a обратная Т на верна, т.к. своб член м. иметь гораздо > делит-й, чем степ многочл. Если своб член имеет много делит-й, то непоср-я проверка этих делит-й на корни многочл треб. б. вычисл-й. Предварительно отсеять части из них позв-т Т₂: Если f(x) ÎZ[x] и a-корень f(x), то f(1) (a-1), а f(-1) (a+1). Док-во: Т.к. a-корень, то f(x)=(х-a)g(x). g(x)ÎZ[x], т.к. если бы коэф-ты g(x) были дробными нашлось бы такое знач х₀ что g(x₀)Ï Z, но тогда рав-во f(x₀)=(х₀-a)g(x₀) не вып-ся => g(x)ÎZ[x]. Возьмем х=1, тогда f(1)=(1-a)g(1) => f(1) -(1-a)=a-1. Если х=-1, то f(-1)=(-1-a)g(-1) => f(-1) (a +1) Обратное не верно. 2) дробные корни Для их нахожд польз-ся след теор-ми Т₁: Многочл с цел коэф, старш коэф кот-го =1, не имеет дроб корней f(x)=xⁿ+a₁x^n-1+…+a_n, a₀=1, a_iÎZ. Метод от против i =1-n. Допустим, что p/q –корень f(x) и (p,q)=1, тогда f(p/q)= (p/q)ⁿ+ a₁(p/q)^n-1+…+a_n=0. Домножим на q^n-1: pⁿ/q=-(a₁p^n-1+a₂p^n-2q+…+a_nq^n-1). Тогда в левой части получ несокр дробь, а в правой целое число. Что невозм. Т₂: Если p/q, где (p,q)=1 – корень многочл f(x)=a₀xⁿ+…a_n то a_n p, a₀ q. Док-во: Пусть p/q – корень f(x), тогда f(p/q)= a₀(p/q)ⁿ+ a₁(p/q)^n-1+…+a_n=0 домножим на qⁿ: a₀pⁿ+a₁p^n-1q+…+a_nqⁿ=0, a₀pⁿ=-q(a₁p^n-1+…+a_nq^n-1) => a₀pⁿ q, т.к. (p,q)=1, получим a₀ q a_nqⁿ=-p(a₀p^n-1+…+a_n-1q^n-1) => a_nqⁿ p, т.е. a_n p. Опред: Многочл назыв непривод-м над полем P, если он имеет только 2 кл. делителей 1-й класс: aÎP, P-поле; 2-й: af(x) над полем рацион чисел м. построить многочл любой степ, неприводимые над полем Q. Это=>из критерия Эйзенштейна: Критерий неприводимости Эйзенштейна: Если из многочл f(x)ÎZ[x]: 1)старш коэф 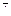p, 2)все остальные коэф p, 3) своб член делится на p, но не / на p², где p-простое число, тогда f(x) неприводим над Q. Док-во: f(x)=a₀xⁿ+…a_nÎZ[x]. Допустим, что f(x) приводим т.е. f(x)=(b_kx^k+…+b₀)(c_tx^t+…+c₀) Сравним коэф правой и лев части при одинаковых степенях неизв-го: (1) a₀=b₀c₀ p, 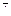p², (2) a₁=b₁c₀+b₀c₁ p, (3) a₂=b₂c₀+b₁c₁+b₀c₂ p, … (n+1) a_n=b_kc_t 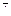p. Из рав-ва (1)=>b₀c₀ p, 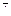p²=>b₀ p или c₀ p. Пусть b₀ p, тогда c₀ 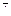p, т.к. b₀c₀ 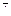p². Из рав-ва (2)=>b₁c₀ p, т.к. с₀ 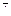p, то b₁ p, …, из (n+1)=>b_k p или a_n p, что приводит к противор с усл-м. Аналогично рассм случай, когда c₀ p. Итак, f(x) неприводим над полем Q.