
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение. Дополнительным к событию А называется событие , означающее, что событие А не происходит
Определение. Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.
Совокупность всех элементарных исходов опыта называется пространством элементарных событий.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события  образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Определение. Противоположными называются два несовместных события, образующие полную группу.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Следствие 2: Сумма вероятностей противоположных событий равна единице.

Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Определение. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

Также можно записать: 
Если события независимые, то  , и теорема умножения вероятностей принимает вид:
, и теорема умножения вероятностей принимает вид:
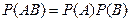
В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.

Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.
Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

Здесь событие А обозначает наступление хотя бы одного из событий Ai, а qi – вероятность противоположных событий  .
.
Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.
Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.
Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.
Всего в колоде 13 червонных и 13 бубновых карт.
При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна  , при вытаскивании второй карты -
, при вытаскивании второй карты -  , третьей -
, третьей -  , четвертой -
, четвертой -  .
.
Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна  .
.
Тогда 
Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?
Вероятность выпадения 6 очков при одном броске кости равна  . Вероятность того, что не выпадет 6 очков -
. Вероятность того, что не выпадет 6 очков -  . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна
. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна  .
.
Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна  .
.
Формула полной вероятности.
Пусть некоторое событие А может произойти вместе с одним из несовместных событий  , составляющих полную группу событий. Пусть известны вероятности этих событий
, составляющих полную группу событий. Пусть известны вероятности этих событий  и условные вероятности наступления события А при наступлении события Hi
и условные вероятности наступления события А при наступлении события Hi  .
.
Теорема. Вероятность события А, которое может произойти вместе с одним из событий  , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.

Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.
Вероятность того, что выстрелы производит первый, второй или третий стрелок равна  . Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
. Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
- для первого стрелка: 
- для второго стрелка: 
- для третьего стрелка: 
Искомая вероятность равна:

Формула Байеса. (формула гипотез)
Пусть имеется полная группа несовместных гипотез  с известными вероятностями их наступления
с известными вероятностями их наступления  . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности  .
.
Требуется определить какие вероятности имеют гипотезы  относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности  .
.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
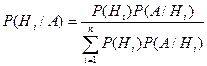
Эта формула называется формулой Байеса.
Пример. Трое охотников одновременно выстрелили по медведю, который был убит одной пулей. Определить вероятность того, что медведь был убит первым стрелком, если вероятности попадания для этих стрелков равны соответственно 0,3, 0,4, 0,5.
В этой задаче требуется определить вероятность гипотезы уже после того, как событие уже совершилось. Для определения искомой вероятности надо воспользоваться формулой Бейеса. В нашем случае она имеет вид:

В этой формуле Н1, Н2, Н3 – гипотезы, что медведя убьет первый, второй и третий стрелок соответственно. До произведения выстрелов эти гипотезы равновероятны и их вероятность равна  .
.
P(H1/A) – вероятность того, что медведя убил первый стрелок при условии, что выстрелы уже произведены (событие А).
Вероятности того, что медведя убьет первый, второй или третий стрелок, вычисленные до выстрелов, равны соответственно:



Здесь q1 = 0,7; q2 = 0,6; q3 = 0,5 – вероятности промаха для каждого из стрелков, рассчитаны как q = 1 – p, где р – вероятности попадания для каждого из стрелков.
Подставим эти значения в формулу Байеса:

Повторение испытаний.
Формула Бернулли.
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.
Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рт,п того, что в результате п испытаний событие А наступило ровно т раз.
Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик)
Пусть в результате п независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие  с вероятностью
с вероятностью  .
.
Обозначим Ai – наступление события А в испытании с номером i. Т.к. условия проведения опытов одинаковые, то эти вероятности равны.
Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

Вероятность каждой комбинации равна произведению вероятностей:
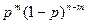
Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:

Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.
Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.
В случае пяти попаданий из пяти возможных: 
Четыре попадания из пяти выстрелов: 
Три попадания из пяти: 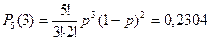
Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
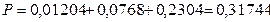
Наивероятнейшее число наступления события 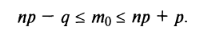





 имеет место
имеет место

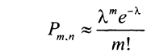





Где 
 и
и 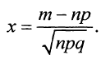















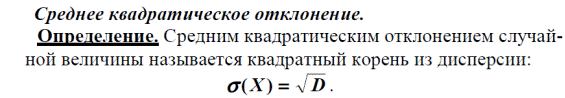

Пример 1










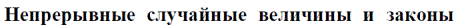



p(a≤X<b)=F(b)-F(a)

Пример 2 
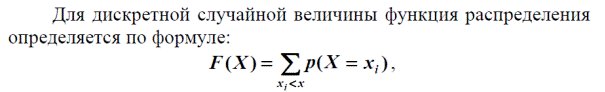

В примере1:





вал: p(30<X<70)=p(30≤X<70)-p(30)=F(70)-F(30)-p(30)=0,4-0,1-0,2=0,1


В примере 2:  и
и 





В примере 2 найдем:










Примеры случайных величин
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [ a, b ], если ее плотность имеет следующий вид


Непрерывная случайная величина Х имеет показательное распределение, если функция плотности которой задается выражением


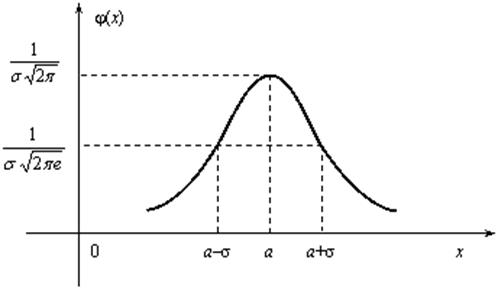
Случайная величина Х имеет нормальное распределение (или распределение по закону Гаусса), если ее плотность вероятности имеет вид: 
Из колоды в 36 карт вытаскивают три. Какова вероятность того, что среди вынутых карт нет десяток
2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7.
Найти: 1) вероятность р того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего
3. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом?
Элементы математической статистики




Date: 2016-02-19; view: 543; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |