Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

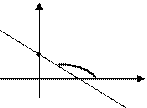
Уравнение прямой с угловым коэффициентом
|
у = kx + b

(!) Не существует для прямых, параллельных оси О у
+ Уравнение пучка прямых: y-y1=k(x-x1)
2) Общее уравнение прямой
|


3)Уравнение прямой с данным вектором нормали
и проходящей через данную точку
|


4)Уравнение прямой в отрезках
|
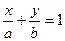
(!) Не существует для прямых,
параллельных осям координат
5) Уравнение прямой, проходящей через две данные точки



|

Вопрос 8: Расстояние от точки до прямой с доказательством.
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу
| d = | |A·Mx + B·My + C| |
| √A2 + B2 |
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
 (1)
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
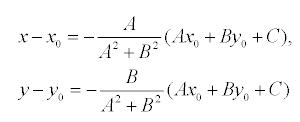
Подставляя эти выражения в уравнение (1), находим:
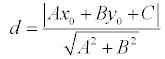
Воспрос 9 Угол между прямыми на плоскости и в пространстве. Условие параллельности и перпендикулярности прямых.
1) На плоскости
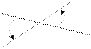 Углом между двумя прямыми I и II называется угол, отсчитываемый в положительном направлении от прямой I к прямой II.
Углом между двумя прямыми I и II называется угол, отсчитываемый в положительном направлении от прямой I к прямой II.
Пусть даны две прямые, заданные уравнениями с угловыми коэффициентами
y = k1 · x + b1, y = k2 · x + b2.
Найдем угол между первой и второй прямыми. Обозначим углы наклона прямых j1 и j2. Тогда k1 = tgj1, k2 = tgj2
Проведем через точку пересечения прямую, параллельную оси OX.

|

- формула для вычисления угла между двумя прямыми.
1. Предположим, что прямые параллельны:
a= 0Þ tg a= 0Þ
k1 = k2 - условие параллельности прямых.
Для случая, когда прямые заданы уравнениями в общем виде: 
2. Предположим, что прямые перпендикулярны:
a= 900 Þ tg a не существует Þ ctg a = 0 Þ
Þ k1 · k2 = -1 - условие перпендикулярности прямых.
Если уравнения прямых заданы в общем виде: 
2) В пространстве
· Определение. Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
·  Угол между прямыми в пространстве равен углу между их направляющими векторами
Угол между прямыми в пространстве равен углу между их направляющими векторами  . Поэтому, если две прямые заданы каноническими уравнениями вида
. Поэтому, если две прямые заданы каноническими уравнениями вида  и
и  то косинус угла между ними можно найти по формуле:
то косинус угла между ними можно найти по формуле:
§ l1|| l2, когда S1|| S2, т.е 
§ l1 ⊥ l2, когда S1⊥S2, т.е 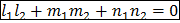
Вопрос 10. Все виды уравнения плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей.
Всякое уравнение вида Ax+By+Cz+D=0, где A, B, C и D –действительные числа (А, В и C не равны 0), определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида Ax+By+Cz+D=0.
 Существуют такие формы записи уравнения плоскости:
Существуют такие формы записи уравнения плоскости:
1) Ax+By+Cz+D=0−общее уравнение плоскости P, где N=(A,B,C)
 2) A(x−x0)+B(y−y0)+C(z−z0)=0− уравнение плоскости, которая проходит через точку M(x0,y0,z0) ⊥вектору N=(A,B,C).
2) A(x−x0)+B(y−y0)+C(z−z0)=0− уравнение плоскости, которая проходит через точку M(x0,y0,z0) ⊥вектору N=(A,B,C).
 3)
3)  - уравнение плоскости в отрезках на осях, где a, b и c− величины отрезков, которые плоскость отсекает на осях координат.
- уравнение плоскости в отрезках на осях, где a, b и c− величины отрезков, которые плоскость отсекает на осях координат.
4)  − уравнение плоскости, которая проходит через три точки A(x1,y1,z1),B(x2,y2,z2) и C(x3,y3,z3).
− уравнение плоскости, которая проходит через три точки A(x1,y1,z1),B(x2,y2,z2) и C(x3,y3,z3).
5) xcosα+ycosβ+zcosγ−p=0− нормальное уравнение плоскости, где cosα,cosβ и cosγ− направляющие косинусы нормального вектора N, направленного из начала координат в сторону плоскости, а p>0−расстояние от начала координат до плоскости.
6*) Ax+By+Cz+D=0: • D=0, Ax+By+Cz=0, плоскость проходит через начало координат • А=0, By+Cz+D=0, N⊥0x плоскость || оси 0x • B=0, N⊥0y,плоскость || оси 0y • C=0, N⊥0z, плоскость || оси 0z • A;D=0, N⊥0x, плоскость проходит через Ox • B;D=0, N⊥0y, плоскость проходит через Oy • C;D=0, N⊥0z, плоскость проходит через Oz • A;B=0, N⊥0xy, плоскость || плоскости Oxy • A;C=0, N⊥0xz, плоскость || плоскости 0xz • B;C=0, N⊥0yz, плоскость || плоскости 0yz • A;B;D=0, N⊥0xy, плоскость совпадает с плоскостью 0xy • A;C;D=0, N⊥0xz, плоскость совпадает с плоскостью 0xz • B;C;D=0, N⊥0yz, плоскость совпадает с плоскостью 0yz
Угол между плоскостями:
Пусть  ={A1;B1;C1} и
={A1;B1;C1} и  ={A2;B2;C2} – нормали к плоскостям α1 и α2, соответственно, тогда угол между плоскостями определяется соотношением:
={A2;B2;C2} – нормали к плоскостям α1 и α2, соответственно, тогда угол между плоскостями определяется соотношением:  =
= 
А условие параллельности и перпендикулярности имеют вид:
α1 || α2 Þ 
 Þ
Þ 
α1 ⊥α2 Þ 
 Þ
Þ 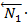
 =0 Þ
=0 Þ 
Вопрос 11. Все виды уравнения прямой в пространстве. Угол между прямыми. Угол между прямой и плоскостью.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0;
2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями:
 =
=  ;
;
3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором 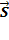 (m, n, р), ей коллинеарным (||) (S-направляющий вектор). Тогда прямая определяется уравнениями:
(m, n, р), ей коллинеарным (||) (S-направляющий вектор). Тогда прямая определяется уравнениями:
 . - каноническое уравнениями прямой.
. - каноническое уравнениями прямой.
Поскольку направляющий вектор S || исследуемой прямой, то равенство нулю какой-либо его координаты означает, что прямая  соответствующей оси. Если две координаты вектора S = 0, то прямая
соответствующей оси. Если две координаты вектора S = 0, то прямая  -на соответствующей координатной плоскости
-на соответствующей координатной плоскости
Угол между прямыми: Углом между двумя прямыми называют угол между направляющими векторами  ={m1;n1;P1} и
={m1;n1;P1} и  ={m2;n2;p2} этих прямых. Этот угол вычисляется по формуле:cosфи =
={m2;n2;p2} этих прямых. Этот угол вычисляется по формуле:cosфи =  =
= 
Угол между прямой и плоскостью:
Плоскость заается вектором нормали 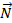 {A,B,C}, а прямая направляющим вектором
{A,B,C}, а прямая направляющим вектором  {m,n,p}, то угол между прямой и плоскостью определяется через синус угла:
{m,n,p}, то угол между прямой и плоскостью определяется через синус угла:
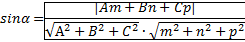
Воспрос 12. Уравнение и свойства эллипса (окружности как частный случай) Свойства фокальных радиусов с доказательством.
· Эллипс - геометрическое место всех точек такое, что сумма расстояний от любой выбранной точки до фокуса постоянно.
 В специально подобранной декартовой системе координат каноническое уравнение эллипса имеет вид:
В специально подобранной декартовой системе координат каноническое уравнение эллипса имеет вид:
 , где |OA1|=|OA2|=a
, где |OA1|=|OA2|=a
|OB1|=|OB2|=b
a,b – полуоси эллипса; F1(-c;0) и F2(c;0) – фокусы эллипса
фокусное расстояние 2с связано с полуосями соотношением: 
E (эксцентреситет) =  - показывает вытянутость, 0≤ E≤1(у окружности =0)
- показывает вытянутость, 0≤ E≤1(у окружности =0)
Расстояние от точки M(x;y), кот принадлежит эллипсу, до фокуса называется фокальным радиусом r1=a+Ex, r2=a-Ex




· Начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ, при a < b фокусы эллипса лежат на оси ОY, а при a = b эллипс становится окружностью (фокусы эллипса в этом случае совпадают с центром окружности). Таким образом, окружность есть частный случай эллипса.
Свойства эллипса:
· Эллипс пересекает каждую из осей координат в двух точках.
· Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси
· Эллипс имеет две взаимно перпендикулярные оси симметрии.
· Эллипс имеет центр симметрии.
· Эллипс может быть получен сжатием окружности.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
 .
.
Воспользуемсяформулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
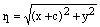 ,
,  , откуда получаем:
, откуда получаем:
 .
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
 .
.
Сокращая, получаем:
 .
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
 .
.
Возводим в квадрат
 .
.
Раскрываем скобки и сокращаем на  :
:
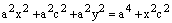 ,
,
откуда получаем:
 .
.
Используя равенство (2), получаем:
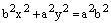 .
.
Разделив последнее равенство на  , получаем равенство (4), ч.т.д.
, получаем равенство (4), ч.т.д.
Date: 2016-02-19; view: 754; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |