Первая теорема Больцано-Коши. Формулировка, доказательство, анализ, применение

Формулировка:

Если функция f(x) определена и непрерывна в [a;b], и f(a) * f(b) < 0 (a и b имеют разные знаки), то $ с є (a;b): f(c) = 0.

Доказательство №1(Больцано):

Для определенности, пусть f(a) < 0, f(b) > 0. Разделим промежуток [a; b] пополам точкой .

Может случиться, что В таком случае, теорема доказана. В противном случае, получим два промежутка: и , причём на концах одного из этих промежутков, функция будет принимать значения разных знаков. Более того, слева – отрицательное значение, справа – положительное. Выберем этот промежуток, обозначив его, как . Разделим его пополам точно так же, как и в прошлый раз, но на этот раз точкой . Опять может произойти такое, что в этой точке функция обращается в нуль. В таком случае теорема доказана. Рассмотрим обратный случай: получаем два промежутка: и . Причём, как и в прошлый раз, на концах одного из этих промежутков, функция будет принимать значения разных знаков. Более того, слева – отрицательное значение, справа – положительное. Выберем этот промежуток, обозначив его, как . Продолжим процесс построения промежутков. При этом мы либо за конечное число шагов придём к точке, в которой f(x) действительно обращается в нуль, либо же получим бесконечную последовательность вложенных один в другой промежутков. В первом случае функция обращается в нуль и теорема доказана. Остановимся на втором. В этом случае, для n-ного промежутка будем иметь:

причём его длина, очевидно, равна:

.

Построенная последовательность промежутков удовлетворяет условиям леммы о вложенных промежутках, так как, учитывая (2): , поэтому существует точка c є [a;b], для которой справедливо равенство:

Осталось только показать, что именно эта точка c удовлетворяет условию теоремы. Перейдём к пределам в неравенствах (1), учитывая непрерывность функции:

и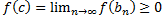

Следовательно, f(c) = 0, что и требовалось доказать.

Доказательство №2(Коши):

Для доказательства тем способом, который предложил Коши, необходимо сформулировать такую лемму:

Если функция f(x) непрерывна в точке x =x₀ и f(x₀) ¹ 0, то для всех достаточно близких к x₀ значений x функция f(x) имеет тот же знак, что и в f(x₀).

Для определенности, пусть f(a) < 0, f(b) > 0. Рассмотрим все точки 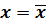, в которых К их числу, например, относится точка a и все близлежащие к ней точки (в силу леммы). Множество ограничено сверху числом b. Положим теперь c =sup{ }; мы утверждаем, что f(c) = 0.

Допустим противное: тогда либо f(c) < 0, либо f(c) > 0. Если бы f(c) < 0, то – по лемме – и правее нашлись бы значения , для которых верно а это противоречило бы определению c, как верхней границы для . Если же было бы f(c) > 0, то снова имели бы - и вблизи c слева, а именно – в некотором достаточно малом промежутке а тогда там вовсе и не было бы значений , что также невозможно, ибо c, по определению – точная верхняя граница для множества . То есть, f(c) = 0, что и требовалось доказать.

Анализ:

Методы, используемые для доказательства теоремы по Больцано:

· Сужение области (метод половинного деления или метод Больцано);

· Индукция;

· Приведение задачи к другой, уже решенной, задаче;

· Перебор вариантов.

Методы, используемые для доказательства теоремы по Коши:

· От противного;

· Перебор вариантов;

· Приведение задачи к другой, уже решенной, задаче;

· Введение вспомогательного элемента.

Условия теоремы являются необходимыми. Докажем это:

1)Исключим первое условие. В таком случае, имея разрыв, функция может сменить знак и, не обращаясь в ноль. Так будет, например, с функцией , на промежутке [-1;1]. Действительно, функция имеет разрыв при , следовательно, первое условие – не выполняется. Также верно и то, что на концах промежутка, функция имеет значения разных знаков: , следовательно, второе условие выполняется. Однако, функция меняет знак и без обращения в 0, что легко доказать: предположим обратное – пусть f(x) имеет значение 0, на заданном промежутке. Попробуем найти значения x, при которых f(x)= = 0. Для этого составим уравнение: . Так как уравнение не имеет корней, то во всем множестве вещественных чисел нет такого значения x, для которого было бы справедливо равенство f(x) = 0, следовательно, в заданном промежутке такого значения нет и подавно.

Из этого следует, что условие №1 является обязательным.

2)Исключим второе условие. В таком случае, функция также может и не обращаться в ноль. Так будет, например, с функцией 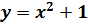, на промежутке [-10; 5]. Действительно функция определена и непрерывна на всём промежутке, из чего следует, что первое условие выполняется. Кроме того, на концах промежутка функция принимает значения одинаковых знаков, следовательно, условие №2 не выполняется. И действительно, в таком случае заключение теоремы становится неверным, так как во всем множестве вещественных чисел нет такого значения x, для которого было бы справедливо равенство f(x) = 0, следовательно, и в заданном промежутке такого значения также нет.

Из этого следует, что условие №2 является обязательным.

Применение:

· Используется для доказательства второй теоремы Больцано – Коши, кроме того, является её частным случаем.

Date: 2016-02-19; view: 4252; Нарушение авторских прав