
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сформулировать все теоремы о числовых последовательностях. Доказать одну из них
Теорема 1. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
Доказательство. Пусть  – бесконечно малая последовательность. Это означает, что для любого положительного числа
– бесконечно малая последовательность. Это означает, что для любого положительного числа  существует такой номер N, что для всех номеров
существует такой номер N, что для всех номеров  выполняется условие
выполняется условие  , где С – любое действительное число. Тогда
, где С – любое действительное число. Тогда  <
<
<  , а это и означает, что последовательность
, а это и означает, что последовательность  – бесконечно малая.
– бесконечно малая.
Теорема 2. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть  и
и  – бесконечно малые последовательности. Это означает, что для любого числа
– бесконечно малые последовательности. Это означает, что для любого числа 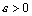 существуют такие номера
существуют такие номера  и
и  , что для всех номеров
, что для всех номеров  и для всех номеров
и для всех номеров  выполняются условия
выполняются условия  и
и  соответственно. Тогда для всех номеров
соответственно. Тогда для всех номеров  выполняется условие
выполняется условие 
 , а это и означает, что последовательность
, а это и означает, что последовательность  – бесконечно малая.
– бесконечно малая.
Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3. Бесконечно малая последовательность ограничена.
Доказательство. Пусть  – бесконечно малая последовательность, ε>0 – некоторое число, а N – номер, начиная с которого выполняется условие
– бесконечно малая последовательность, ε>0 – некоторое число, а N – номер, начиная с которого выполняется условие  . Обозначим через М наибольшее из следующих чисел
. Обозначим через М наибольшее из следующих чисел  . Очевидно, что
. Очевидно, что  для любого номера n, а это и означает, что последовательность {
для любого номера n, а это и означает, что последовательность {  } – ограничена.
} – ограничена.
Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
Доказательство. Пусть  – ограниченная, а
– ограниченная, а  – бесконечно малая последовательности. Это означает, что существует число М >0 такое, что для любого номера n выполняется
– бесконечно малая последовательности. Это означает, что существует число М >0 такое, что для любого номера n выполняется  , и для любого числа
, и для любого числа  существует номер N такой, что для всех номеров
существует номер N такой, что для всех номеров  выполняется
выполняется  . Тогда для всех номеров
. Тогда для всех номеров  и любого ε>0 выполняется
и любого ε>0 выполняется  , а это и означает, что последовательность
, а это и означает, что последовательность  – бесконечно малая.
– бесконечно малая.
Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 5. Если элементы бесконечно малой последовательности  равны одному и тому же числу С, то С =0.
равны одному и тому же числу С, то С =0.
Доказательство. Предположим, что 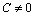 . Для
. Для  существует такой номер N, что для всех номеров
существует такой номер N, что для всех номеров  выполняется
выполняется  . Так как
. Так как  , а
, а  , то последнее неравенство имеет вид
, то последнее неравенство имеет вид  , откуда
, откуда 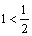 . Полученное противоречие показывает, что предположение
. Полученное противоречие показывает, что предположение 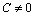 неверно, следовательно,
неверно, следовательно,  .
.
Теорема 6. Если  – бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность
– бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность  , которая является бесконечно малой. Если не все элементы бесконечно малой последовательности
, которая является бесконечно малой. Если не все элементы бесконечно малой последовательности  равны нулю, то последовательность
равны нулю, то последовательность  бесконечно большая.
бесконечно большая.
Доказательство. Пусть  – бесконечно большая последовательность. Это означает, что для любого положительного числа М можно указать такой номер N, что для всех номеров
– бесконечно большая последовательность. Это означает, что для любого положительного числа М можно указать такой номер N, что для всех номеров  выполняется
выполняется  . А это означает, что при
. А это означает, что при  все элементы
все элементы  , а поэтому последовательность
, а поэтому последовательность  имеет смысл с номера N. Пусть
имеет смысл с номера N. Пусть 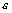 - любое положительное число. Для числа
- любое положительное число. Для числа  можно указать номер
можно указать номер  такой, что для n
такой, что для n  N выполняется
N выполняется  . Это и означает, что
. Это и означает, что  – бесконечно малая. Доказательство второй части теоремы проводится аналогично.
– бесконечно малая. Доказательство второй части теоремы проводится аналогично.
Рассмотрим теперь лемму, которая будет использоваться при доказательстве некоторых теорем.
Лемма. Для того чтобы число а являлось пределом последовательности  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  имел вид
имел вид 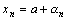 , n =1,2,…, где
, n =1,2,…, где  есть бесконечно малая последовательность.
есть бесконечно малая последовательность.
Доказательство. Обозначим  . Условие
. Условие  по определению предела равносильно тому, что для любого числа
по определению предела равносильно тому, что для любого числа 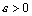 существует такой номер N, что для всех номеров
существует такой номер N, что для всех номеров  выполняется неравенство
выполняется неравенство  , то есть
, то есть  , а это и равносильно тому, что
, а это и равносильно тому, что  .
.
Эта лемма показывает особую роль бесконечно малых последовательностей при изучении предела последовательности. Перейдем теперь непосредственно к рассмотрению простейших свойств пределов числовых последовательностей.
Теорема 7. Числовая последовательность может иметь только один предел.
Доказательство. Предположим противное. Это означает, что существует последовательность  , имеющая два различных предела а и в. По лемме
, имеющая два различных предела а и в. По лемме 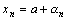 и
и  , где
, где  и
и  – бесконечно малые последовательности, откуда получаем
– бесконечно малые последовательности, откуда получаем 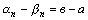 . Так как все элементы бесконечно малой последовательности
. Так как все элементы бесконечно малой последовательности  имеют одно и то же значение в-а, то в-а =0, то есть в=а, что противоречит предположению. Теорема доказана.
имеют одно и то же значение в-а, то в-а =0, то есть в=а, что противоречит предположению. Теорема доказана.
Теорема 8. Сходящаяся числовая последовательность ограничена.
Доказательство. Пусть  – сходящаяся к числу а, тогда
– сходящаяся к числу а, тогда  , где
, где 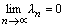 . Так как бесконечно малая последовательность ограничена, то $ такое число
. Так как бесконечно малая последовательность ограничена, то $ такое число 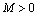 , что для всех
, что для всех  выполняется
выполняется  . Поэтому
. Поэтому 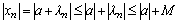 для всех
для всех  , а это и означает, что последовательность
, а это и означает, что последовательность  ограничена.
ограничена.
Теорема 9. Если последовательность  сходится к числу а, то и любая подпоследовательность этой последовательности сходится к этому же числу.
сходится к числу а, то и любая подпоследовательность этой последовательности сходится к этому же числу.
Доказательство. По условию  , то есть для любого числа
, то есть для любого числа  существует такой номер N, что для всех номеров
существует такой номер N, что для всех номеров  выполняется неравенство
выполняется неравенство  . Пусть
. Пусть  – некоторая подпоследовательность последовательности
– некоторая подпоследовательность последовательности  . Тогда для всех номеров
. Тогда для всех номеров  выполняется
выполняется  , поэтому
, поэтому  .
.
Замечание. Теорема 3 справедлива для случая  , то есть для бесконечно большой последовательности
, то есть для бесконечно большой последовательности  . Таким образом, каждая подпоследовательность бесконечно большой последовательности является бесконечно большой последовательностью. Доказательство этого утверждения аналогично доказательству теоремы 3.
. Таким образом, каждая подпоследовательность бесконечно большой последовательности является бесконечно большой последовательностью. Доказательство этого утверждения аналогично доказательству теоремы 3.
Теорема 10. Если последовательность  сходится к числу
сходится к числу  , то, начиная с некоторого номера, определена последовательность
, то, начиная с некоторого номера, определена последовательность  , которая является ограниченной.
, которая является ограниченной.
Доказательство. Пусть  , так как
, так как  . Пусть N – номер, начиная с которого выполняется условие
. Пусть N – номер, начиная с которого выполняется условие  . Отсюда при
. Отсюда при  получаем
получаем  или
или  . Тогда при
. Тогда при 
 , что означает ограниченность последовательности
, что означает ограниченность последовательности  , начиная с номера N.
, начиная с номера N.
Теорема 11. Если  и, начиная с некоторого номера, выполняется
и, начиная с некоторого номера, выполняется 
 , то
, то 
 .
.
Доказательство. Пусть с некоторого номера выполняется  . Предположим, что
. Предположим, что  . Так как
. Так как  , то для
, то для  существует такой номер N, что для всех
существует такой номер N, что для всех  выполняется
выполняется 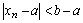 или
или 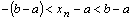 , откуда получаем
, откуда получаем  , что противоречит условию. Случай
, что противоречит условию. Случай  рассматривается аналогично.
рассматривается аналогично.
Следствие 1. Пусть  и
и  сходятся и, начиная с некоторого номера, выполняется
сходятся и, начиная с некоторого номера, выполняется  , тогда
, тогда  .
.
Следствие 2. Пусть  сходится и при любом
сходится и при любом 
 , тогда и
, тогда и  .
.
Доказательство. Так как  , то и
, то и  .
.
Теорема 12. Пусть 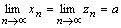 и с некоторого номера n выполняется условие
и с некоторого номера n выполняется условие 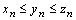 . Тогда последовательность
. Тогда последовательность  сходится и
сходится и  .
.
Доказательство. Пусть  – номер, с которого выполняется
– номер, с которого выполняется 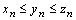 , тогда с этого номера выполняется
, тогда с этого номера выполняется  , или
, или  . Так как
. Так как  и
и  , то для любого числа
, то для любого числа 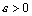 существуют такие номера
существуют такие номера  и
и  , что для всех
, что для всех 
 , а для всех
, а для всех 
 , а для всех номеров
, а для всех номеров  , где
, где  выполняется
выполняется  , что и означает
, что и означает  .
.
Теорема 13. Если монотонная последовательность  ограничена, то она сходится.
ограничена, то она сходится.
Доказательство. Так как последовательность  ограничена, то множество ее элементов имеет точные верхнюю
ограничена, то множество ее элементов имеет точные верхнюю  и нижнюю
и нижнюю  грани. Пусть
грани. Пусть  – неубывающая последовательность и
– неубывающая последовательность и  – точная верхняя грань множества ее элементов. Это означает, что для любого числа
– точная верхняя грань множества ее элементов. Это означает, что для любого числа 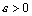 можно указать такой элемент
можно указать такой элемент  , что
, что  и
и  . Эти два неравенства равносильны неравенству
. Эти два неравенства равносильны неравенству  или
или  . Так как
. Так как  – неубывающая последовательность, то при
– неубывающая последовательность, то при  выполняется
выполняется  или
или 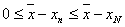 . Это означает, что при
. Это означает, что при  выполняется
выполняется  или
или  . Таким образом,
. Таким образом,  . Аналогично доказывается случай, когда
. Аналогично доказывается случай, когда  – невозрастающая последовательность.
– невозрастающая последовательность.
Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме 8 сходящаяся монотонная последовательность ограничена.
Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность  сходится к числу ноль, но не является монотонной.
сходится к числу ноль, но не является монотонной.
Замечание 3. Если последовательность  неубывающая сходящаяся и
неубывающая сходящаяся и  - ее предел, то для всех номеров n выполняется неравенство
- ее предел, то для всех номеров n выполняется неравенство 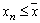 . Аналогично, если
. Аналогично, если  невозрастающая сходящаяся последовательность и
невозрастающая сходящаяся последовательность и  – ее предел, то для всех номеров n справедливо
– ее предел, то для всех номеров n справедливо 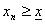 .
.
Определение. Говорят, что последовательность { 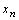 } удовлетворяет условию
} удовлетворяет условию  Коши, если для любого числа
Коши, если для любого числа  >0 существует такой номер N, зависящий от
>0 существует такой номер N, зависящий от  , что для всех номеров m и n таких, что n≥N, m≥N, справедливо неравенство
, что для всех номеров m и n таких, что n≥N, m≥N, справедливо неравенство  <
< 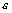 (*).
(*).
Последовательность, удовлетворяющая условию Коши, называется фундаментальной.
Условие (*) можно сформулировать иначе: для любого числа 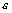 >0 существует такой номер N, зависящий от
>0 существует такой номер N, зависящий от 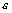 , что для всех номеров n
, что для всех номеров n  N и всех натуральных p выполняется условие:
N и всех натуральных p выполняется условие:  .
.
Теорема (критерий Коши). Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Доказательство. Необходимость. Пусть последовательность {  } сходится и
} сходится и  .
.
Зададим 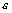 >0, тогда существует такой номер N, что для всех номеров n
>0, тогда существует такой номер N, что для всех номеров n  N выполняется неравенство
N выполняется неравенство  . Пусть n
. Пусть n  N и m
N и m  N, тогда
N, тогда  , то есть выполняется условие Коши.
, то есть выполняется условие Коши.
Достаточность. Пусть { 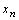 } удовлетворяет условию Коши, то есть для любого
} удовлетворяет условию Коши, то есть для любого 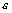 >0 существует номер N, что для n
>0 существует номер N, что для n  N и m
N и m  N выполняется неравенство
N выполняется неравенство 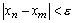 . Пусть
. Пусть 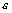 =1, тогда существует номер N
=1, тогда существует номер N  такой, что при n
такой, что при n  N
N  и m
и m  N
N  выполняется
выполняется  . В частности, если n
. В частности, если n  N
N  и m=N
и m=N  , то
, то 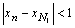 , то есть
, то есть  при n
при n  N
N  . Это значит, что последовательность {x
. Это значит, что последовательность {x  }, n=N
}, n=N  , N
, N  +1,…ограничена. Поэтому в силу теоремы Больцано-Вейерштрасса существует ее сходящаяся подпоследовательность {
+1,…ограничена. Поэтому в силу теоремы Больцано-Вейерштрасса существует ее сходящаяся подпоследовательность {  }.
}.
Пусть  . Зададим
. Зададим 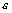 >0. Тогда существует такой номер K
>0. Тогда существует такой номер K  ,что для всех номеров K
,что для всех номеров K  K
K  или, что то же самое, для всех n
или, что то же самое, для всех n  n
n  выполняется неравенство
выполняется неравенство 
Обозначим через  =max{ N,n
=max{ N,n  } и зафиксируем некоторое n
} и зафиксируем некоторое n 
 . Тогда для всех n
. Тогда для всех n  N имеем
N имеем  , что и означает, что
, что и означает, что 
Date: 2016-02-19; view: 706; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |