
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общие указания
Задания и методические рекомендации
По выполнению контрольной работы
по дисциплине «Математический анализ»
(для студентов направления «Экономика»
заочной формы обучения)
Курган - 2011
Задания и методические рекомендации по выполнению контрольной работы по дисциплине «Математический анализ» (для студентов направления «Экономика» заочной формы обучения) составлены:
· с учётом требований Федерального Государственного образовательного стандарта высшего профессионального образования к минимуму содержания и уровню подготовки выпускников по направлению;
· на основании учебного плана подготовки бакалавров по данному направлению.
Задания и методические рекомендации по выполнению контрольной работы по дисциплине «Математический анализ» (для студентов направления «Экономика» заочной формы обучения) разработала:
ст. преподаватель кафедры МиЕНД_______________/ Макеева Н.В./
Задания и методические рекомендации по выполнению контрольной работы по дисциплине «Математический анализ» (для студентов направления «Экономика» заочной формы обучения) утверждены на заседании кафедры МиЕНД
Протокол №2 от «8» сентября 2011 г.
Заведующий кафедрой МиЕНД
к. ф. – м. наук, доцент________________________/Косовских С.В. /
Общие указания
В курсе «Математический анализ» студенты-заочники 1 курса изучают дифференциальное и интегральное исчисления, дифференциальные уравнения и ряды. Изучение этих разделов математики занимает важное место в формировании экономиста высокой квалификации и служит теоретической основой многих специальных учебных дисциплин. На втором году обучения студенты-заочники изучают математическое программирование, теорию вероятностей и математическую статистику. Знание этих разделов математики имеет большое значение при решении вопросов, связанных с организацией и планированием производства. Это необходимо для общей экономической подготовки студентов, создания у них прочной базы независимо от области, в которой они в будущем будут работать. В методических указаниях к каждой контрольной работе приводится список рекомендованной учебной литературы, изучение которой необходимо для выполнения заданий. Указываются номера глав и параграфов учебников, а также номера задач, предназначенных для самостоятельной работы. В случае возникновения затруднений студент может обратиться на кафедру высшей математики за письменной консультацией. Необходимо строго придерживаться следующих правил:
1. Студент обязан делать работу только своего варианта, отсылая ее в Академию на рецензирование в сроки, предусмотренные графиком!
2. Контрольную работу следует выполнять на листах формата А4 чернилами любого цвета, кроме красного или в печатном виде.
3. В конце работы необходимо привести список использованных источников.
4. Перед решением задачи нужно полностью выписать ее условие. Если несколько задач имеют общую формулировку, переписывать следует только условие задачи нужного варианта.
Решение каждой задачи студент должен сопровождать подробными объяснениями и ссылками на соответствующие формулы, теоремы и правила. Вычисления должны быть доведены до конечного числового результата. Ответы и выводы, полученные при решении задач, следует подчеркнуть.
5. После получения отрецензированной работы студенту необходимо исправить все отмеченные ошибки и недочеты. Если работа не зачтена, то следует переделать те задачи, на которые указывает рецензент, а при отсутствии такого указания вся контрольная работа должна быть выполнена заново. Переделанная работа высылается на повторное рецензирование обязательно с не зачтенной ранее работой и рецензией к ней. При этом на обложке следует указать фамилию рецензента. Работы, выполненные без соблюдения этих правил, к зачету не принимаются и возвращаются без рецензирования для переработки. При подготовке к экзамену следует еще раз обратиться к методическим указаниям и примерам, разобранным в них, вопросам для самопроверки и задачам, которые рекомендуется решить. На экзамен студент должен являться с зачтенными контрольными работами и рецензиями на них. Каждому студенту предлагается индивидуальное задание, состоящее из пяти задач в каждой из четырех контрольных работ. Для определения индивидуального задания контрольной работы 1 нужно использовать таблицу 1.
Номера задач контрольных работ определяются по соответствующей таблице с помощью двух последних цифр номера зачетной книжки студента.
Например, для студента, имеющего зачетную книжку с номером ЗЭ 87128, на пересечении горизонтальной колонки 2 и столбца 8 таблицы 1 указаны следующие номера задач его индивидуального задания контрольной работы 1: 08, 21, 54, 66, 83.
Таблица 1
ДЛЯ ОПРЕДЕЛЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
КОНТРОЛЬНОЙ РАБОТЫ № 1
| Последняя цифра номера зачетной книжки | |||||||||||
| П Р Е Д П О С Л Е Д Н Я Я Ц И Ф Р А | |||||||||||
КОНТРОЛЬНАЯ РАБОТА
ПРОГРАММА
Раздел I.Введение в анализ: множества, функции
Тема 1. Действительные числа, их свойства. Числовые множества. Элементы алгебры множеств. Обозначения для сумм и произведений. Окрестность точки. Ограниченные множества.
Тема 2. Числовые функции. Способы задания функций. Область определения и множество значений функции. График функции. Сложная и обратная функции. Характеристики функций: четность и нечетность, периодичность, монотонность, ограниченность. Свойства основных элементарных функций. Степенная, показательная и логарифмическая функции. Тригонометрические функции и обратные к ним. Элементарные функции.
Раздел II.Предел и непрерывность
Тема 1. Числовые последовательности. Способы задания последовательностей. Прогрессии. Формула сложных процентов. Предел последовательности и его свойства. Единственность предела. Ограниченность сходящейся последовательности. Бесконечно малые и бесконечно большие последовательности, их свойства. Свойства пределов, связанные с арифметическими действиями.
Тема 2. Предел функции. Различные типы пределов: односторонние пределы, пределы в бесконечности, бесконечные пределы. Бесконечно малые и бесконечно большие функции, их свойства. Свойства пределов, связанные с арифметическими действиями и с неравенствами. Первый и второй замечательные пределы. Замена переменной при вычислении предела (предел сложной функции). Сравнение бесконечно малых функций: эквивалентные функции.
Тема 3. Непрерывность функции в точке. Непрерывность суммы, разности, произведения и частного непрерывных функций. Непрерывность сложной и обратной функции. Непрерывность элементарных функций. Точки разрыва функции, их классификация. Свойства функций, непрерывных на отрезке: теоремы о существовании корня, о промежуточных значениях, об ограниченности функции, о достижении наибольшего и наименьшего значений.
Раздел III.Дифференциальное исчисление функций одной переменной
Тема 1. Производная функции. Дифференцируемость и дифференциал
функции. Непрерывность дифференцируемой функции. Геометрический смысл производной и дифференциала функции. Уравнение касательной к графику функции. Правила дифференцирования суммы, разности, произведения и частного двух функций, сложной и обратной функций. Производные основных элементарных функций. Эластичность функции, ее свойства и геометрический смысл. Логарифмическая производная. Локальный экстремум функции, теорема Ферма. Теоремы Ролля, Лагранжа и Коши для дифференцируемых функций. Правило Лопиталя раскрытия неопределенностей. Производные и дифференциалы высших порядков. Признак монотонности функции на интервале. Достаточное условие локального экстремума.
Тема 2. Исследование функции с помощью производной и построение графика функции. Монотонность функции. Экстремумы функции. Выпуклые (вогнутые) функции. Достаточные условия выпуклости функции. Необходимый и достаточный признаки точки перегиба. Асимптоты графика функции. Отыскание наибольшего и наименьшего значений функции на отрезке.
Раздел IV.Интегральное исчисление функций одной переменной
Тема 1. Первообразная и неопределенный интеграл. Таблица неопределенных интегралов. Свойства неопределенного интеграла. Замена переменной в неопределенном интеграле, интегрирование по частям. Интегрирование рациональных функций. Интегрирование некоторых классов иррациональных и трансцендентных функций.
Тема 2. Определенный интеграл и его свойства. Интегрируемость непрерывной функции. Интеграл с переменным верхним пределом. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле, интегрирование по частям. Геометрические приложения определенного интеграла: вычисление площади криволинейной трапеции и объема тела вращения. Несобственные интегралы.
Раздел V.Дифференциальное исчисление функции нескольких переменных
Тема 1. Функции нескольких переменных. Поверхности (линии) уровня
функции. Предел и непрерывность функции нескольких переменных. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений. Частные производные, дифференцируемость, дифференциал функции нескольких переменных. Достаточное условие дифференцируемости. Непрерывность дифференцируемой функции. Производная сложной функции. Производная по направлению, градиент. Свойства градиента. Эластичность функции нескольких переменных. Частные производные высших порядков. Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Условный экстремум функции нескольких переменных. Метод исключения переменных. Метод множителей Лагранжа. Нахождение глобальных экстремумов дифференцируемой функции на замкнутом ограниченном множестве.
Раздел VI.Обыкновенные дифференциальные уравнения
Тема 1. Обыкновенные дифференциальные уравнения первого порядка, их решения. Задача Коши. Общее и частное решения уравнения. Общий интеграл. Уравнения первого порядка, интегрируемые в квадратурах: с разделяющимися переменными, однородные, в полных дифференциалах,
линейные, Бернулли.
Тема 2. Линейные дифференциальные уравнения. Пространство решений линейного однородного уравнения, фундаментальная система решений. Структура общего решения линейного неоднородного уравнения. Линейные дифференциальные уравнения с постоянными коэффициентами (на примере уравнений второго порядка). Характеристическое уравнение и фундаментальная система решений однородного уравнения. Построение частного решения неоднородного уравнения с правой частью специального вида методом неопределенных коэффициентов.
Раздел VII.Ряды
Тема 1. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Числовые ряды с неотрицательными членами: критерий и признаки сходимости (первый и второй признаки сравнения, признак Даламбера в предельной форме, интегральный признак). Знакочередующиеся ряды. Признак Лейбница. Оценка остатка ряда. Абсолютно и условно сходящиеся числовые ряды. Свойства абсолютно и условно сходящихся рядов.
Тема 2. Степенные ряды. Интервал и радиус сходимости степенного ряда. Свойства степенного ряда на интервале сходимости. Ряды Тейлора (Маклорена). Разложимость в ряд Тейлора бесконечно дифференцируемой функции с производными, ограниченными в совокупности. Разложения функций ex, sin x, cos x, (1+ x)a, ln(1+ x) в ряд Маклорена.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Указания составлены в соответствии с учебниками [1, 2, 3]
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Уч. пособие для вузов. Ч.1,2.-М.: ОНИКС 21 век, 2002
2.Кремер Н.Ш. Высшая математика для экономистов: Учебник для вузов. - 2-е изд., перераб. и доп.-М.: ЮНИТИ, 2004
3.Кремер Н.Ш. Практикум по высшей математике для экономистов: Учеб. пособие для вузов. - М.: ЮНИТИ - ДАНА, 2005
Раздел 1- 2
[1]: гл.6, §§ 1-6.
[2]: гл.5, §§ 1-7, гл.6, §§1-8.
[3]: гл.5, гл.6, §§1-5.
Вопросы для самопроверки
1. Что называется функцией? Каковы способы ее задания?
2. Что называется областью определения функции?
3. Что называется графиком функции?
4. Дайте определение конечного предела функции в точке. Дайте определения конечного предела функции при x →+∞ и при х→-∞.
5. Как связаны понятия: «предел функции в точке» и «пределы функции в точке слева и справа»?
6. Что такое бесконечно малая величина? Сформулируйте основные теоремы о бесконечно малых величинах.
7. Что такое бесконечно большая величина и как она связана с бесконечно малой?
8. Сформулируйте основные теоремы о пределах.
9. Напишите первый и второй замечательные пределы. Какие теоремы о пределах используются при их вычислении?
10. Дайте определения функции, непрерывной в точке и на отрезке.
11. Сформулируйте основные теоремы о непрерывных функциях.
12. Какие типы точек разрыва функции Вы знаете? Приведите примеры.
После получения этих тем можно приступить к выполнению первой задачи контрольной работы.
Задача 1
Найти предел:
3x2 + 11x + 10 x – 1 3 – x/2
а) lim; г) lim;
x→ -2  -
-  x→∞ x + 3
x→∞ x + 3
x (sin 5x + sin 6x) lg (x + 1)
б) lim; д) lim;
x→0  x→0 sin 2x
x→0 sin 2x
tg2 3x
в) lim; е) lim (e3x – e2x) ∙ ctg 4x
x→0  x→0
x→0
Решение:
а) Функция, предел которой при х→ -2 требуется найти, представляет собой частное двух функций. Однако применить теорему о пределе частного ([2], гл.6. § 5 теорема4) в данном случае нельзя, так как предел функции, стоящей в знаменателе, при х→ -2 равен нулю.
Преобразуем данную функцию, умножив числитель и знаменатель дроби, находящейся под знаком предела, на выражение  , сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:
, сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:
3х2 + 11х + 10 (3х + 5)(х + 2)( )
)
= =
 (
( )(
)( )
)
(3х + 5)(х + 2)( ) (3х +5)(х + 2)(
) (3х +5)(х + 2)( )
)
=.
(х + 7) – (3 – х) 2(х + 2)
Сокращая теперь числитель и знаменатель последней дроби на общий множитель х + 2, получим новую функцию (3х + 5)( )
)
у =,
которая отличается от данной значением лишь в одной точке х = -2: данная функция в этой точке не определена, а новая определена и непрерывна как элементарная функция ([2], гл.5, § 3). Поскольку переопределение функции в одной точке не сказывается на значении предела и поскольку для функции, непрерывной в точке х0, ее предел при х→х0 равен значению этой функции в точке х0 ([2], гл.6, §7), то
 .
.
б) И в этом примере начнем преобразования с умножения числителя и знаменателя дроби, стоящей под знаком предела, на выражение, сопряженное к знаменателю:
х(sin 5x + sin 6x) x(sin 5x + sin 6x)( )
)
= =
 (1 + x ∙ tg x) – (1 - x ∙ tg x)
(1 + x ∙ tg x) – (1 - x ∙ tg x)
x(sin 5x + sin 6x)( ) (sin 5x + sin 6x)(
) (sin 5x + sin 6x)( )
)
= = =
2x ∙ tg x 2x ∙ tg x
sin 5x + sin 6x cos x
= ∙ ∙ ( ).
).
sin x 2
Заметим, что пределы в нуле второго и третьего сомножителей как непрерывных в нуле функций равны их значениям в этой точке:
cos x
lim = ½; lim ( ) = 2
) = 2
x→0 2 x→0
Чтобы найти предел первого сомножителя, разделим его числитель и знаменатель на х:
sin 5x + sin 6x sin 5x sin 6x
+
sin 5x + sin 6x x x x
= =
sin x sin x sin x
x x
Предел sin x
lim = 1
x→0 x
есть первый замечательный предел ([2], гл.6, § 6). Пределы  легко сводятся к нему. Например,
легко сводятся к нему. Например, 
и после замены t = 5х:
sin 5x sin t
lim = lim = 1
x →0 5x x →0 t
sin 5x sin 6x
Следовательно, lim = 5. Аналогично, lim = 6. Теперь с помощью теорем о пре-
x →0 x x →0 x
деле частного и суммы ([2], гл.6, § 5, теорема 2,4) вычисляем предел первого сомножителя:
sin 5x sin 6x
lim + lim
sin 5x + sin 6x x →0 x x →0 x 5 + 6
lim = = = 11
x →0 sin x sin x 1
lim
x →0 x
Воспользовавшись, наконец, теоремой о пределе произведения ([2], гл. 6, § 5, теорема 3), окончательно получаем:
sin 5x + sin 6x cos x
lim ∙ ∙ ( ) = 11∙ ½ ∙ 2 = 11
) = 11∙ ½ ∙ 2 = 11
x →0 sin x 2
в) Избавляясь от иррациональности в знаменателе (так же, как и в предыдущих двух примерах) и применяя формулу 1 – cos 2x = 2sin2x, будем иметь:
tg23x tg23x ∙ (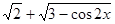 )
)
lim = lim =
x →0  x →0 2 – (3 – cos 2x)
x →0 2 – (3 – cos 2x)
tg23x tg23x
= lim (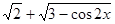 ) = lim (
) = lim (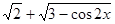 )
)
x →0 cos 2x – 1 x →0 - 2sin2x
Предел в нуле функции у = 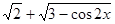 найдем, воспользовавшись непрерывностью этой элементарной функции в нуле:
найдем, воспользовавшись непрерывностью этой элементарной функции в нуле:
lim (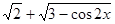 ) =
) = 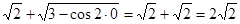
tg23x
Предел в нуде функции у = найдем, разделив предварительно числитель и зна-
-2sin2x
менатель дроби в правой части равенства на х2 и используя основные свойства предела:
tg23x tg3x 2 sin 3x 2
lim lim
tg23x x2 x →0 x x →0 x cos 3x
lim = - ½ ∙ lim = - ½ ∙ = - ½ ∙ =
x →0 -2sin2x x →0 sin2x sin x 2 sin x 2
x2 lim lim
x →0 x x →0 x
sin 3x 3 2
lim ∙
x →0 3x cos 3x sin 3x 3 2 3 2
= - ½ ∙ = - ½ ∙ lim ∙ lim = - ½ ∙ 1 ∙ = - 9/2
12 x →0 3x x →0 cos 3x cos 0
Теперь, применяя теорему о пределе произведения, получим:
tg23x tg23x
lim = lim ∙ lim (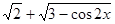 ) =
) = 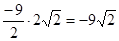
x →0  x →0 -2 sin2 x x →0
x →0 -2 sin2 x x →0
г) Прежде всего преобразуем основание данной степенно-показательной функции:
х – 1 х + 3 – 3 – 1 (х + 3) – 4 4
= = =1-
х + 3 х + 3 х + 3 х + 3
Введем новую переменную

Заметим, что предел функции t при х→+∞ равен нулю, то есть t→0 при х→+∞.
Следовательно, 
В конце мы воспользовались теоремой о пределе произведения, следствием теоремы о пределе сложной функции ([2], гл.6, § 5), вторым замечательным пределом ([2], гл.6, §6) и непрерывностью в нуле функции у = (1 + t)9/2
д) Разделим числитель и знаменатель дроби, стоящей под знаком предела, на х:
lg (x + 1)
lg (x + 1) x
=
sin 2x sin 2x
x
и рассмотрим пределы в нуле числителя и знаменателя получившейся большой дроби:
lg (x + 1) 1
lim = lim tg (x + 1) = lim lg (x + 1)1/ x = lg lim (x + 1)1/ x = lg e
x →0 x x →0 x x →0 x →0
и sin 2x 2sin 2x sin 2x
lim = lim = 2 ∙ lim = 2 ∙ 1 = 2.
x →0 x x →0 2x x →0 2x
Используя, наконец, теорему о пределе частного, получим:
lg (x + 1) lg (x + 1)
lim
x x →0 x lg e
lim = =
x →0 sin 2x sin 2x 2
x lim
x →0 x
е) Представим выражение под знаком предела в виде
ex – 1
cos 4x ex – 1 x
(e3x – e2x ) ∙ ctg 4x = (e2x ex – e2x) ∙ = e2x ∙ ∙ cos 4x = e2x ∙ ∙cos4x
sin 4x sin 4x sin 4x
x
Легко находим: lim e2x = e0 = 1; lim cos 4x = cos 0 = 1;
x →0 x →0
sin 4x 4sin 4x sin 4x
lim = lim = 4 ∙ lim = 4 ∙ 1 = 4
x →0 x x →0 4x x →0 4x
ех - 1
Для вычисления предела функции у = при x →0 введем новую переменную
х
t = ex – 1. Тогда ех = t + 1, x = ln (1 + t) причем предел в нуле непрерывной функции t = ex – 1 равен значению функции в нуле: е0 – 1 = 1 – 1 = 0, то есть t→0 при x →0. Следовательно,
lim 1
ex – 1 t 1 x →0 1 1
lim = lim = lim = = = = 1
x →0 x x →0 ln (1 + t) x →0 1/t ln (1 + t) lim ln (1 + t)1/ t ln lim (1 + t)1/ t ln e
x →0 x →0
Применяя теоремы о пределе произведения и частного, окончательно получаем:
ex – 1
x
lim e2x ∙ ∙ cos 4x = 1∙ ¼ ∙ 1 = ¼
x →0 sin 4x
x
Раздел 3
[1]: гл.7, §§ 1-6.
[2]: гл.7, §§ 1-7; гл.9, §§ 1-3.
[3]: гл.7, §§ 1-4; гл.9.
Вопросы для самопроверки
1. Что называется производной функции? Найдите производную функции у = х3, пользуясь только определением производной.
2. Что называется касательной к кривой в данной точке? Каков геометрический смысл производной? Как составить уравнение касательной?
3. Каков механический смысл производной?
4. Может ли функция иметь производную в точке разрыва?
5. Будет ли функция непрерывна в точке, если она в ней дифференцируема?
6. Перечислите правила дифференцирования и формулы дифференцирования основных элементарных функций.
7. Производная сложной функции.
8. Что называется дифференциалом функции? Его основные свойства.
9. Каков геометрический смысл дифференциала функции в точке при заданном приращении аргумента?
10. Какие свойства дифференциала функции Вы знаете?
11. Сформулируйте теоремы Ролля и Лангранжа.
12. Дайте определение возрастания (убывания) функции. В чем состоит необходимый и достаточный признак возрастания (убывания) функции?
13. Дайте определение максимума (минимума) функции. В чем состоит необходимый признак экстремума?
После изучения этих тем можно приступить к выполнению второй задачи контрольной работы.
Задача 2
5х + 9
Исследовать функцию у = и построить ее график.

Решение
1. Область определения данной функции – вся числовая ось, то есть интервал
(-∞; +∞), так как выражение 5х + 9

в правой части аналитического задания функции имеет смысл при любом действительном х.
2. Как элементарная функция данная функция является непрерывной в каждой точке своей области определения, то есть в каждой точке числовой оси.
3. Найдем все асимптоты графика данной функции.
Вертикальных асимптот график данной функции у = f (x) не имеет, поскольку последняя непрерывна на всей числовой оси ([2], гл.8, § 7).
Для отыскания наклонной асимптоты при х→+∞ вычислим следующие два предела
k = lim y/x и b = lim (y – kx)
x→+∞ x→+∞
Если оба они существуют и конечны, то прямая у = kx + b является наклонной асимптотой при х→+∞ графика функции у = f (x) ([2], гл. 9, § 7).
Прежде чем обращаться к вычислению указанных пределов, напомним тождество  *
*
Приступая к вычислению первого предела, разделим числитель и знаменатель дроби на х2, затем воспользуемся равенством (*) и основными свойствами предела:
5x + 9 5 9 5 9
+ +
y 5x + 9 x2 x x2 x x2 5 ∙ 0 + 9 ∙ 0
k = lim = lim = lim = lim = lim =
x→+∞ x x→+∞ x√x2 + 3 x→+∞ x√x2 + 3 x→+∞ √x2 + 3 x→+∞ √1 + 3/x2 √ 1+ 3 ∙0
x2 x
=0.
Для вычисления второго предела разделим числитель и знаменатель дроби на х и, действуя далее аналогично тому, как и при вычислении первого предела, получим:
5x + 9
5x + 9 x 5 + 9/x 5 + 9 ∙ 0
b = lim (y – kx) = lim y = lim = lim = lim = =
x→+∞ x→+∞ x→+∞ √x2 + 3 x→+∞ √x2 + 3 x→+∞ √1 + 3/x2 √1 + 3 ∙ 0
x
=5.
Следовательно, прямая у = 5 является наклонной асимптотой графика данной функции при х→+∞ (поскольку угловой коэффициент k этой прямой равен нулю, то такую наклонную асимптоту называют также горизонтальной при х→+∞).
Для отыскания наклонной асимптоты при х→-∞ вычислим пределы
k1 = lim y/x и b1 = lim (y – kx)
х→+∞ х→+∞
Если оба они существуют и конечны, то прямая y = k1x + b1 является наклонной асимптотой при х→-∞.
Для вычисления этих пределов используем те же приемы, что и выше, учитывая только на сей раз, что  . Теперь, в частности, для отрицательных значений аргумента имеем:
. Теперь, в частности, для отрицательных значений аргумента имеем:
√х2 + 3 √х2 + 3 х2 + 3 3
= = -√ = - √ 1 +
х -√х х2 х2
и следовательно, k1 = 0, b1 = -5

то есть наклонной (горизонтальной) асимптотой при х→-∞ на сей раз является прямая у = -5. Изобразим пунктиром найденные асимптоты на предварительном чертеже (рисунок2):
Рисунок 2
4. Найдем точки пересечения графика данной функции с осями координат и установим участки ее знакопостоянства.
Для отыскания абсцисс точек пересечения графика с осью ОХ решим уравнение
5х + 9
= 0

Его единственным решением, очевидно, является х = -1,8. Причем, в силу положительности знаменателя при любом х ясно, что
f (x) > 0 при х > -1,8
f (x) < 0 при х < -1,8
Таким образом, точка А (-1,8; 0) является единственной точкой пересечения графика функции с осью ОХ, а для х из интервалов (-∞; -1,8) и (-1,8; +∞) соответствующие точки графика функции расположены, соответственно, ниже и выше оси абсцисс.
Точка пересечения графика функции у = f (x) с осью ОУ – это всегда точка (0; f(0)), если только нуль входит в область определения функции. В нашем случае такой точкой является
В (0; 9/√3), где 9/√3= 9√3/3 = 3√3 ≈ 5,20.
Полученные в результате исследования точки А и В изобразим на предварительном чертеже (рисунок 2)
5. Приступим теперь к отысканию точек экстремума данной функции и участков ее монотонности.
Вычислим сначала ее производную:
5√х2 + 3 – (5х + 9) х
√х2 + 3 5(х2 + 3) – х(5х + 9) 3(5 –3х)
у/ = = =
х2 + 3 (х2 + 3) √х2 + 3 (х2 + 3) ½
Решая уравнение у/ = 0, получим единственный корень производной: х = 5/3 ≈ 1,67
Таким образом, необходимое условие экстремума ([2], гл.8,§ 4) выполняется лишь в точке
х = 5/3. Эта точка разбивает ось абсцисс на два интервала (-∞; 5/3) и (5/3; +∞)
знакопостоянства производной. Для определения знака производной в каждом интервале (пользуясь ее непрерывностью) определим знак производной в одной какой-либо точке каждого интервала. Так как 15 -3
f/(0) = > 0 и f/(2) = < 0
√27 √343
то заключаем, что функция возрастает на интервале (-∞; 5/3) и убывает на интервале
(5/3; +∞), и значит точка х = 5/3 является точкой максимума данной функции ([2], гл.8 § 4). Значение функции в этой точке (то есть максимум функции) равно
5 ∙ 5/3 + 9 52
f (5/3) = = = √52 ≈ 7.21
√(5/3)2 + 3 √52
Отметим на чертеже вершину С (5/3; √52) графика данной функции (рисунок 2).
6. Наконец, обратимся к исследованию данной функции на выпуклость, вогнутость и существование точек перегиба.
С этой целью найдем производную второго порядка данной функции:
-3(х2 + 3)3/2 – (5 – 3х) ∙ 3/2 ∙ (х2 + 3) ½ ∙ 2х 3(х2 + 3) ½ [-(х2 + 3) – х(5 – 3х)]
у/ = (у)/ = 3 ∙ = 3 ∙
(х2 + 3)3 (х2 + 3)3
9(2х2 – 5х – 3)
=
(х2 + 3)5/2
Решая затем уравнение у// = 0, эквивалентное квадратному уравнению 2х2 – 5х – 3 = 0, находим его корни: х1 = -0,5; х2 = 3, которые разбивают область определения функции на три интервала знакопостоянства второй производной: (-∞; -0,5), (-0,5; 3), (3; +∞). Для определения знака производной второго порядка в каждом из этих интервалов определим ее знак в какой-либо точке соответствующего интервала:
9 ∙ (2 + 5 - 3)
f//(-1) = = 9/8 > 0
√(1 + 3)5
9 ∙ (-3) 27 3
f//(0) = = - = - = -√3 < 0
√35 9√3 √3
9 ∙ (32 – 20 – 3) 81
f//(4) = = > 0
√195 192 √19
Из полученных неравенств вытекает, что график функции является выпуклым на интервале
(-0,5; 3) и вогнутым на интервалах (-∞; -0,5) и (3; +∞) ([2], гл.8 § 6), и значит точки
D (-0,5; f(-0.5)) и Е (3; f(3)), согласно определению ([2], гл.8 § 6), являются точками перегиба графика данной функции. Осталось найти ординаты этих точек:
-5/2 + 9 13
f (-0,5) = = = √13 ≈ 3,61
√1/4 + 3 √13
15 + 9 24 12
f (3) = = = = 4√3 ≈ 6,93
√9 + 3 2√3 √3
Точки D и E также отметим на рисунке 2.
Учитывая результаты полного исследования, соединим непрерывной кривой все ранее отмеченные точки предварительного чертежа так, чтобы эта кривая слева и справа неограниченно приближалась к асимптотам у = -5 и у = 5, соответственно (рисунок3)

Рисунок 3. Искомый график функции.
Раздел 4
[1]: глава 9, §§ 1-5.
[2]: глава 10, §§ 1-9.
[3]: глава 10, §§ 1-6.
Вопросы для самопроверки
1. Какая функция называется первообразной данной функции?
2. Что называется неопределенным интегралом от данной функции?
3. Запишите таблицу простейших интегралов.
4. Как производится замена переменной в неопределенном интеграле?
5. Как производится интегрирование по частям в неопределенном интеграле?
6. Назовите основные свойства неопределенного интеграла.
7. Что называется определенным интегралом от данной функции? Каков его геометрический смысл?
8. Как связаны между собой понятия определенного и неопределенного интеграла?
9. Сформулируйте теорему о производной определенного интеграла с переменным верхним пределом.
10. Перечислите основные свойства определенного интеграла.
11. Дайте определение несобственных интегралов с бесконечным пределом интегрирования.
После разбора этих тем можно приступать к выполнению третьей задачи контрольной работы.
Задача 3
Вычислить площадь фигуры, ограниченной линиями у = х2 – 2 х и у = -2 х2 + х.
Решение:
Чтобы наглядно представить фигуру, площадь которой надо найти, построим графики функций у = х2 – 2 х и у = -2 х2 + х в одной системе координат.

Рисунок 1
Для построения параболы у = х2 – 2 х определим координаты ее вершины и точек пересечения с осями координат. Выделив полный квадрат у = х2 – 2 х = (х – 1)2 – 1, получим координаты вершины параболы А (1; -1). Ветви параболы направлены вверх, так как коэффициент при х 2, равный 1, положителен. Точки пересечения параболы с осью абсцисс найдем, решив квадратное уравнение х2 – 2 х = 0. Корни этого уравнения х 1 = 0; х 2 = 2. Получили точки О (0; 0); А (2; 0). Точка пересечения с осью ординат находится при х = 0. Эта точка совпадает с точкой А. Для построения второй параболы у =-2 х2 + х необходимо провести аналогичные действия. Получим вершину В (1/4; 1/8) и точки О (0; 0); В 1 (½; 0). Ветви этой параболы направлены вниз, так как коэффициент при х 2 отрицателен. На рисунке 4 построены обе параболы. Заштрихованная часть плоскости является фигурой, площадь которой надо найти. Для определения абсцисс точек пересечения парабол решим уравнение х2 – 2 х = -2 х2 + х или
3 х 2 – 3 х = 0, откуда х 1 = 0; х 2 = 1.
Площадь фигуры вычислим по формуле
b
S = ∫ [ f (x) – g (x)] dx, где f (x) ≥ g (x) для всех x € [a; b]
a
(формула (11.21) §6 главы 11 [2]).
В нашем случае а = х 1 = 0; b = x 2 = 1. На отрезке [0; 1] имеем: -2 х 2 + х ≥ х 2 – 2 х.
Поэтому f (x) = -2x2 + x и g (x) = x2 – 2x.
Следовательно,
1 1
S = ∫ [(-2x2 + x) – (x2 – 2x)] dx = ∫ (-3x2 + 3x) dx
1 0
Для вычисления определенного интеграла применяется формула Ньютона-Лейбница:
b b
∫ f (x) dx = F (x) = F (b) – F (a),
a a
где F (x) – первообразная подынтегральной функции f (x) (формула (11.15) § 4 главы 11 [2]).
Окончательно
1 1
S = ∫ (-3x2 + 3x) dx = (-x3 + 3/2 x2) = -(1)3 + 3/2 ∙ 1 – 0 = ½
0 0
Ответ: 0,5 кв.ед.
Раздел 5
[1]: глава 8, §§ 1- 4.
[2]: глава 15, §§ 1-12.
[3]: глава 15, §§ 1-6.
Вопросы для самопроверки
1. Дайте определение непрерывной функции нескольких (например, двух) переменных.
2. Дайте определение частных производных и полного дифференциала. Как они связаны?
3. Что называется градиентом функции нескольких переменных?
4. Дайте определение экстремума функции нескольких переменных и приведите необходимые условия экстремума.
5. Как определяются частные производные?
После изучения этих тем можно приступать к выполнению четвертой задачи контрольной работы.
Задача 4
Найти z//yx ; z//yy ; z//xy ; z//xx функции z = 3х + х2 у3. Написать уравнение линий уровня
f (x; y) = c при c = 0 и с = 1. Найти grad z в точке М0 (-1; 1).
Решение:
Учитывая формулы (15.1) и (15.2) § 3 главы 15 [2] и обычные правила дифференцирования функции одной переменной, находим частные производные первого порядка. При этом следует помнить, что при вычислении частной производной по х, мы считаем у постоянной. Аналогично, при нахождении частной производной по у считаем х постоянной.
∂ z ∂
z/x = = (3x + x2 y2) = 3 + 2xy3
∂ x ∂ x
∂ z ∂
z/y = = (3x + x2 y2) = 0 + 3x2 y2 = 3x2 y2
∂ y ∂ y
Теперь найдем частные производные второго порядка:
∂2 z ∂
z//xx = (z/x)/x = = (3 + 2xy6 ) = 0 + 2y3 = 2y3
∂ x2 ∂ x
∂2 z ∂
z//yy = (z/y)/y = = (3x2 y2 ) = 6x2 y
∂ y2 ∂ y
∂
z//xy = (z/x)/y = (3 + 2xy3 ) = 0 + 6xy2 = 6xy2
∂ y
∂
z//yx = (z/y)/x = (3x2 y2 ) = 3y2 ∙ 2x = 6xy2
∂ x
Запишем уравнения линий уровня. Как известно, линии уровня образуют на плоскости семейство параллельных кривых, на каждой из которых функция принимает постоянное значение
f (x; y) = с.
При с = 0 имеем линию нулевого уровня: 3х + х2 у3 = 0.
При с = 1 уравнение линии уровня: 3х + х2 у3 = 1
При переходе от одной линии уровня к другой значение функции изменяется.
∂ z ∂ z
Направление возрастания функции указывает вектор grad z =;
∂ x ∂ y
Найдем направление градиента в точке М0 (-1; 1). Имеем
∂ z ∂ z
M0 = 3 + 2 ∙ (-1) ∙ (1)3 = 1; M0 = 3 ∙ (-1)2 ∙ 12 = 3.
∂ x ∂ x
Поэтому grad z = {1; 3} в точке М0.
Раздел 6
[1]: глава 4, § 1-5 (часть 2).
[2]: глава 12, § 1-9.
[3]: глава 12, § 1-7.
Вопросы для самопроверки
1. Дайте определение дифференциального уравнения и основных понятий, связанных с ним (порядок решения, общее решение, частное решение и интегральная кривая).
2. Как можно геометрически истолковать общее и частное решение?
3. Изложите методы решения основных типов дифференциальных уравнений первого порядка (с разделяющимися переменными, однородных и линейных).
4. Изложите методы решения основных типов дифференциальных уравнений второго порядка (с понижением порядка, однородных и линейных).
После разбора этих тем можно приступить к выполнению пятой задачи контрольной работы.
Задача 5
Найдите решение дифференциального уравнения у // + 4 у / + 3 у = е –2 х , удовлетворяющее начальным условиям у (0) = 2, у / (0) = 0.
Решение
В соответствии с теоремой 3 §8 главы 12 книги [2] общее решение данного неоднородного линейного уравнения есть сумма его частного решения и общего решения соответствующего ему линейного однородного дифференциального уравнения у // + 4 у / + 3 у = 0.
Ищем общее решение однородного уравнения. В соответствии с формулами 12.38 из § 8 главы 12 книги [2] это решение записывается в виде у 0 = С1 ек1х + С ек2х, где С1 и С2 – произвольные постоянные, а k 1 и k 2 – корни характеристического уравнения ak 2 + bk + c = 0 данного уравнения ay // + by / + cy = 0. В нашем случае а = 1, b = 4, c = 3. Характеристическое уравнение принимает вид: k 2 + 4 k + 3 = 0, его корни k 1 = -3, k 2 = -1, значит, общее решение однородного уравнения имеет вид: у 0 = С1 е-3х + С2 е-х.
Найдем частное решение неоднородного уравнения. Поскольку правая часть данного уравнения содержит в показателе степени коэффициент (-2), не являющийся корнем характеристического уравнения, частное решение следует искать в виде: у 1 = de –2x. Найдем неизвестный коэффициент d. Так как у/ 1 = 2 de –2x, у// 1 = -4 de –2x, подставив значения у1, у/1, у//1 в данное уравнение, получим равенство 4 de –2x – 8 de –2x + 3 de –2x = e –2x откуда – de –2x = e –2x, т.е.
d = -1.
Таким образом, общее решение данного дифференциального уравнения имеет вид
у = у0 + у1 = С1 е –3х + С2 е –х – е –2х
Найдем то решение, которое удовлетворяет данным начальным условиям. Так как
у/ = -3 С1 е –3х + С2 е –х – 2е –2х, у (0) = С1 + С2 – 1, у/ (0) = -3 С1 – С2 + 2,
то решая систему уравнений: С1 + С2 – 1 = 2, -3 С1 – С2 = 0, находим С1 = -0,5; С2 = 3,5.
Следовательно, у = -0,5 –3х + 3,5е –х – е –2х - искомое решение.
Ответ: у = -0,5 –3х + 3,5е –х – е –2х
Задачи 01-20
Найти предел:
01.
а)  в)
в) 
б) 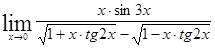 г)
г) 
02.
а)  в)
в) 
б)  г)
г) 
03.
а)  в)
в) 
б)  г)
г) 

04.
а)  в)
в) 
б) 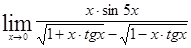 г)
г) 
05.
а)  в)
в) 
б)  г)
г) 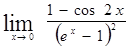
06.
а)  в)
в) 
б)  г)
г) 
07.
а)  в)
в) 
б)  г)
г) 
08.
а)  в)
в) 
б) 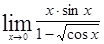 г)
г) 

09.
а)  в)
в) 
б)  г)
г) 
10.
а)  в)
в) 
б)  г)
г) 
11.
а)  в)
в) 
б)  г)
г) 
12.
а)  в)
в) 
б) 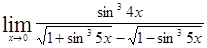 г)
г) 
13.
а)  в)
в) 
б)  г)
г) 

14.
а)  в)
в) 
б)  г)
г) 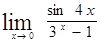
15.
а)  в)
в) 
б)  г)
г) 
16.
а) 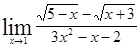 в)
в) 
б)  г)
г) 
17.
а)  в)
в) 
б)  г)
г) 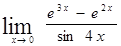
18.
а)  в)
в) 
б)  г)
г) 

19.
а)  в)
в) 
б)  г)
г) 
20.
а)  в)
в) 
б)  г)
г) 
Задачи 21-40
Исследовать функцию у = f (x) и построить ее график:
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 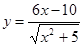
29.  30.
30. 
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 
39.  40.
40. 
Задачи 41-60
Вычислить площадь фигуры, ограниченной линиями
у = ах2 + bx и у = сх2 + dx
| Номер | a | b | c | d |
| -1 | -1 | |||
Date: 2016-02-19; view: 331; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |