Примеры решения типовых задач. Пример 1. Изменить порядок интегрирования в двойном интеграле

Пример 1. Изменить порядок интегрирования в двойном интеграле

Решение. Зная пределы интегрирования, найдем границы области интегрирования D: и построим их (рис. 2). Область D располагается в полосе 0£ x £1 и ограничена снизу и сверху соответствующими ветвями параболы y²=4x.

Найдем новые пределы внешнего (по у) и внутреннего (по х) интегрирования. Так как область D проецируется на ось Оу в отрезок АВ, то пределами внешнего интегрирования являются ординаты точек А и В, т. е. у=-2 и y=2 соответственно. Левой границей области является кривая х = у²/4 (урав нение параболы у²=4х разрешено относительно х), а правой - прямая х=1. Таким образом, двойной интеграл I с измененным порядком интегрирования запишется в виде

Пример 2. Вычислить тройной интеграл,

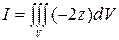если область V ограничена поверхностями s₁: z=2 и s₂ : z²=x²+y² (z³0) (рис. 3).

Решение. Исключая z из уравнений s₁ и s₂, получим уравнение границы области D_xy (проекции V на плоскость хОу): х²+y²= 4. Для вычисления интеграла I переходим к цилиндрическим координатам по формулам (4) с пределами интегрирования 0£j£2p, 0£r£2, r£z£2 (z=r - уравнение верхней части конуса z² = x² + y² в цилиндрических координатах). По формуле (5) получаем

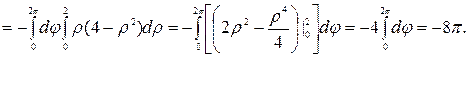Пример 3. Вычислить поверхностный интеграл

где s₂ - внешняя часть конуса z² = х²+у^г (z ≤ 0), отсекаемая плоскостью z=2 (рис. 13).

Решение. Поверхность s₂ однозначно проецируется в область D_xy плоскости хОу и интеграл вычисляется по формуле (7).

Единичный вектор внешней нормали к поверхности s₂ найдем по формуле (8):

Здесь в выражении для нормали выбран знак плюс, так как угол g между осью Oz и нормалью - тупой и, следовательно, должен быть отрицательным. Учитывая, что , на поверхности s₂ , получаем

Область D_xy есть круг Поэтому в последнем интеграле переходим к полярным координатам (при этом 0£j£2p, 0£r£2):

Пример 4. Найти дивергенцию и ротор векторного поля

Решение. По формуле (9) получаем

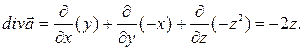Ротор данного векторного поля находим по формуле (10):

Пример 5. Вычислить поток векторного поля через замкнутую поверхность s, образованную плоскостью z=2 и частью конуса (z³0). Проверить результат с помощью формулы Остроградского.

Решение. Поверхность s состоит из двух поверхностей: s₁-части плоскости z=2 и s₂ – части конуса (рис. 13). Поэтому поток через s равен сумме потоков вектора через составляющие поверхности:

где 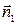и 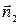- внешние нормали к плоскости и конусу соответственно.

Для поверхности z=2 в силу формулы (8) получим и, следовательно,

так как на поверхности s₁ имеем z=2.

Вычислим поток через поверхность s₂, уравнение которой в явном виде дается соотношением 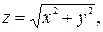вектор внешней нормали равен

По формуле (11) получаем

(см. пример 3).

Таким образом, поток векторного поля через поверхность равен

Найдем решение этой задачи с помощью формулы Остроградского (13). Дивергенция поля равна (см. пример 4), и поток

как это было показано в примере 2.

Пример 6. Вычислить циркуляцию векторного поля по контуру Г, образованному пересечением поверхностей s₁: z=2 и s₂: (z³0). Проверить результат с помощью формулы Стокса.

Решение. Пересечением указанных поверхностей является окружность z=2 (рис. 13). Направление обхода контура выбирается обычно так, чтобы ограниченная им область оставалась слева. Запишем параметрические уравнения контура Г:

				(15)

откуда

причем параметр t изменяется от 0 до 2p. По формуле (12) с учетом (6) и (15) получаем

Ц

Применим теперь формулу Стокса (14). В качестве поверхности s₁, натянутой на контур Г, можно взять часть плоскости z=2. Направление нормали к этой поверхности согласуется с направлением обхода контура Г. Ротор данного векторного поля вычислен в примере 4: Поэтому искомая циркуляция

Ц

что совпадает со значением циркуляции, полученным непосредственно вычислением.

2.2. Контрольная работа № 5

Задача 25

Построить область интегрирования и изменить порядок интегрирования.

№ вар.	Данный интеграл	№ вар.	Данный интеграл

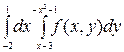
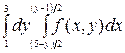
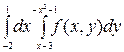
Задача 26

Найти координаты центра тяжести однородной пластины, ограниченной линиями. Сделать чертеж.

№ вар.	Уравнения линий	№ вар.	Уравнения линий

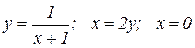
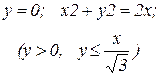
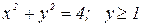
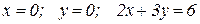
Задача 27

Перейдя к полярным координатам, вычислить двойной интеграл. Сделать чертеж.

№ вар.	Данный интеграл	Область интегрирования D

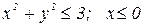
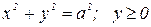
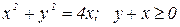
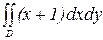
Задача 28

Вычислить объем тела, ограниченного заданными поверхностями. Сделать чертеж.

№ вар.	Уравнения поверхностей	№ вар.	Уравнения поверхностей

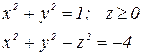
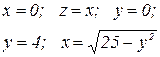
Задача 29

Требуется:

1) найти поток векторного поля через замкнутую поверхность (выбирается внешняя нормаль к );

2) вычислить циркуляцию векторного поля по контуру L, образованному пересечением поверхностей и (направление обхода выбирается так, чтобы область, ограниченная контуром L находилась слева);

3) проверить правильность вычисленных значений потока и циркуляции с помощью формул Гаусса и Стокса;

4) дать заключение о наличии источников или стоков внутри области, ограниченной поверхностью ;

5) сделать чертеж поверхности .

№ вар.	Векторное поле	Поверхности

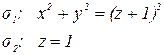
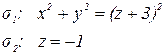
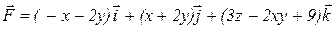
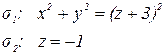
Вопросы к экзамену

1. Что называется двойным интегралом от функции по области ? Укажите его геометрический смысл.

2. Докажите теорему о среднем для двойного интеграла и укажите её геометрический смысл.

3. Выведите формулу для вычисления двойного интеграла с помощью двукратного. Обоснуйте формулы, служащие для вычисления объёма цилиндрического тела и площади плоской фигуры с помощью двойных интегралов.

4. Как выразить элемент площади области и двойной интеграл в полярных координатах? Выведите формулу для вычисления двойного интеграла в полярных координатах с помощью двукратного.

5. Каков геометрический смысл интеграла , где - функция, обладающая непрерывными частными производными в области ? Вычислите площадь поверхности сферы . Используйте полярные координаты.

6. Каков механический смысл интеграла , где 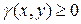- непрерывная функция в области ?

7. Выведите формулу для вычисления координат центра тяжести плоской фигуры , поверхностная плотность которой .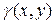

8. Что называется тройным интегралом от функции 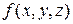по пространственной области V? Укажите его механический смысл.

9. Что называется трёхкратным интегралом от функции 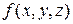по области V? Как он вычисляется?

10. Сформулируйте теорему о среднем для тройного интеграла. Выведите формулу для вычисления тройного интеграла с помощью трёхкратного.

11. Обоснуйте формулу, служащую для вычисления объёма тела с помощью тройного интеграла.

12. Как выразить элемент объёма области и тройной интеграл в цилиндрических координатах? Напишите формулу для вычисления тройного интеграла в цилиндрических координатах с помощью трёхкратного.

13. Каков механический смысл интеграла 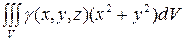, где - непрерывная функция в области ? Напишите формулу для вычисления координат центра тяжести тела , объёмная плотность которого .

14. Что называется криволинейным интегралом по координатам? Укажите его механический смысл. Сформулируйте известные Вам свойства криволинейного интеграла.

15. Как обозначается криволинейный интеграл от векторного поля по кривой ? Что называется циркуляцией векторного поля по замкнутому контуру ?

16. Дайте определение дивергенции векторного поля и перечислите её дифференциальные свойства. Запишите формулы дивергенции в цилиндрической и сферической системах координат.

17. Дайте определение ротора векторного поля и перечислите его дифференциальные свойства. Запишите формулы ротора в декартовых координатах и в ортогональных криволинейных координатах.

18. Что называется потоком векторного поля через двустороннюю поверхность? Перечислите основные свойства и методы вычисления потока.

19. Сформулируйте теорему Остроградского. Выведите из формулы Остроградского инвариантный смысл дивергенции векторного поля.

20. Какие векторные поля называются потенциальными? Дайте определение соленоидального векторного поля.

РЯДЫ

Литература: [2], гл.9; [3], гл.4, 6, §6.9, 6.10; [4], т.2, гл. XVI, XVII; т.I гл. VII, §4, 5; [5], гл. XVII; [8], гл. 5,9,11.