Задача № 2. Расчет пластинки на изгиб

На прямоугольную пластинку (рисунок 21) с размерами в плане a = b = 4м действует поперечная нагрузка

В качестве функции прогиба предлагается выражение:

Требуется:

1 Найти постоянный коэффициент «С» из условия, что предложенная функция w (x,y) удовлетворяет уравнению изгиба пластинки (17).

2 Установить, каким граничным условиям удовлетворяет предложенное уравнение упругой поверхности w (x,y).

3 Составить выражения моментов и поперечных сил по известным формулам для этих усилий (18) – (20).

4 Построить эпюры моментов и поперечных сил для заданных сечений

I – I и II – II. (В контрольной работе эпюры строятся для одного сечения).

Решение.

1 Для выяснения граничных условий найдем выражения для прогибов, углов поворота и изгибающих моментов на кромках пластинки (см. параграф «Запись условий опирания») Вначале вычислим соответствующие производные от функции прогиба:

, ,

,

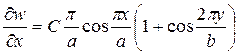На левой грани (ее координаты: x = 0, - b/ 2≤ y ≤ b/ 2) и на правой грани (x = а, -b/ 2≤ y ≤ b/ 2) прогиб w = 0. (Для выяснения этого достаточно подставить координаты кромок в уравнение прогиба). То есть кромки оперты.

Угол поворота на этих гранях 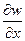принимает значения:

при х = 0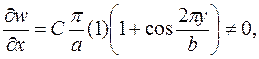

при х = а

Пока можно сделать вывод что кромки не защемлены.

Вычисляем изгибающие моменты

,

т. е. левая и правая кромки шарнирно оперты.

На верхнем (0 ≤ x ≤ a, y = b/ 2) и нижнем (0 ≤ x ≤ a, y = - b/ 2) краях пластинки прогиб w = 0.

Угол поворота на этих гранях определяется как и принимает значения:

при y = b /2

при y = - b/ 2

Таким образом, верхняя и нижняя кромки защемлены.

2 Для вычисления константы «С» находим соответствующие уравнению (17) производные и подставляем в уравнение изгиба пластинки.

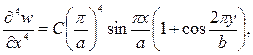
После подстановки полученных производных и выражения q (x, y) в уравнение (17) и приведения подобных членов получим:

Сокращая на общий множитель определяем постоянную С:

3 Находим выражения для моментов и поперечных сил с учетом полученных производных и постоянной «С».

(а)

(б)

(в) (г)

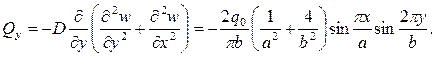(д)

4. Для построения эпюр внутренних усилий в сечении I-I с координатами 0 ≤ х ≤ а, у = – b/ 4 = – 1м подставим в полученные выше выражения постоянное значение у = – b/ 4 = – 1м. Тогда в этих выражениях внутренних усилий

Уравнения (а) – (д) представляют собой уравнения синусоид и косинусоид с одной полуволной и разными амплитудами. Для построения эпюр необходимо вычислить значения минимум в трех точках.

Соответствующие вычисления сведем в таблицу 5.

Примем коэффициент Пуассона μ = 0,3.

Таблица 5

Внутренние усилия	Координата «х»
х = 0	х = а/ 2 = 2 м	х = а = 4 м
Мх
Му
Мху
Qx
Qy

Сечение II-II. х = а/ 2, - b/ 2≤ y ≤ b/ 2 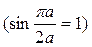. Значения соответствующих внутренних усилий сведем в таблицу 6.

Таблица 6

Внутренние усилия	Координата «у»
у = - b/ 2 = - 2 м	y = 0	у = b/ 2 = 2 м
Мх
Му
Мху
Qx
Qy

Поскольку Q_y (см. выражение (д)) вдоль оси у имеет две полуволны синусоиды для уточнения решения вычислим Q_y при у = ± b /4.

Строим эпюры прогибов и внутренних усилий (рисунок 19).

Список литературы

Основной:

1 Александров А. В. и др. Сопротивление материалов. М.: Высш. шк., 1995.

2 Варданян Г. С. И др. Сопротивление материалов с основами теории упругости и пластичности. М.: АСВ. 2000.

3 Теребушко О. И. Основы теории упругости и пластичности., М.: Наука, 1984.

Дополнительной:

1 Нечипорук Г. С. Решение плоской задачи теории упругости с применением ПЭВМ (учебное пособие)., Магадан,: МфХГТУ. 1997.

2 Самуль В. И. Основы теории упругости и пластичности., М.: Высш. шк. 1982.

3 Тимошенко С. П., Гудъер Дж. Теория упругости., М.: 1979.

4 Сопротивление материалов с основами теории упругости и пластичности. Методические указания для студентов инженерно-строительных специальностей., М.: Высш. шк. 1990.

Оглавление

Постановка задачи теории упругости ……………………………………….……3

Плоская задача теории упругости в декартовых координатах…………….…….4

Плоская задача теории упругости в полярных координатах…………………….7