
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейные дифференциальные уравнения 1-го порядка
Общий вид этих уравнений следующий:  . Поясним, почему это уравнение является линейным относительно у и у ¢. Обратите внимание, какие операции производятся над ними в уравнении. Переменная у умножается на функцию, зависящую только от х. То же действие выполнено и с у ¢. Нет в уравнении ни у 2, ни уу ¢, никаких других функций от этих переменных. Обе они входят только в первой степени, т.е. линейно. Отсюда и название уравнения.
. Поясним, почему это уравнение является линейным относительно у и у ¢. Обратите внимание, какие операции производятся над ними в уравнении. Переменная у умножается на функцию, зависящую только от х. То же действие выполнено и с у ¢. Нет в уравнении ни у 2, ни уу ¢, никаких других функций от этих переменных. Обе они входят только в первой степени, т.е. линейно. Отсюда и название уравнения.
Существует готовая формула общего решения этого уравнения. Но она слишком громоздка для математически неподготовленного человека. Рассмотрим метод Бернулли для решения линейного уравнения. Он заключается в том, что решение уравнения ищется в виде произведения двух новых неизвестных функций:  или короче
или короче  . Для решения также понадобится заготовка
. Для решения также понадобится заготовка  . Далее, в исходное линейное уравнение подставим вместо символа у произведение
. Далее, в исходное линейное уравнение подставим вместо символа у произведение  , а вместо символа
, а вместо символа  заготовку
заготовку 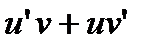 . Получим дифференциальное уравнение относительно новых неизвестных функций
. Получим дифференциальное уравнение относительно новых неизвестных функций  и
и  .
.

Раскроем скобки:
 .
.
Из левой части этого уравнения возьмем два слагаемых: одно обязательно с произведением  , а второе с символом
, а второе с символом  и создадим из них новое дифференциальное уравнение:
и создадим из них новое дифференциальное уравнение:
 или
или  .
.
Вариант, когда  , интереса не представляет, т.к. в этом случае и функция
, интереса не представляет, т.к. в этом случае и функция  . Поэтому получаем уравнение
. Поэтому получаем уравнение  .
.
Замечание. Если приглядеться, то левая часть этого нового уравнения с точностью до обозначения неизвестной функции удивительно напоминает левую часть исходного линейного дифференциального уравнения. Это означает, что функция  -- не что иное, как частное решение однородного линейного уравнения, получающегося из неоднородного заменой правой части
-- не что иное, как частное решение однородного линейного уравнения, получающегося из неоднородного заменой правой части  на ноль.
на ноль.
Все дальнейшие действия разберем на конкретном примере.
Пример 19. Найти решение дифференциального уравнения  , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию  .
.
Решение. Для перехода к новому дифференциальному уравнению заменим в исходном уравнении символ у на произведение uv, а символ у¢ на сумму 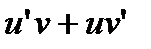 . Получим уравнение
. Получим уравнение
 (1)
(1)
Из подчеркнутых слагаемых создаем новое уравнение  . Сократим его на
. Сократим его на  . Останется уравнение
. Останется уравнение 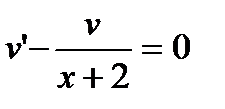 . А это дифференциальное уравнение с разделяющимися переменными. Решим его.
. А это дифференциальное уравнение с разделяющимися переменными. Решим его.
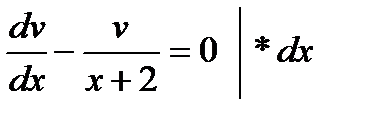 Þ
Þ  Þ
Þ  Þ
Þ  Þ
Þ  .
.
Для нахождения  нам нужна только одна конкретная функция
нам нужна только одна конкретная функция  , поэтому нужно выбрать только одно конкретное значение константы С, например, С = 0. Тогда
, поэтому нужно выбрать только одно конкретное значение константы С, например, С = 0. Тогда
 .
.
Вернемся в уравнение (1). Функция  найдена нами так, что сумма подчеркнутых слагаемых обращается в ноль, а значит, из уравнения эти слагаемые исчезают. При этом вместо буквы v нужно подставить выражение
найдена нами так, что сумма подчеркнутых слагаемых обращается в ноль, а значит, из уравнения эти слагаемые исчезают. При этом вместо буквы v нужно подставить выражение  :
:  .
.
По ОДЗ исходного дифференциального уравнения  , а значит, на него все уравнение можно сократить, после чего получится
, а значит, на него все уравнение можно сократить, после чего получится  . Найдем
. Найдем
 .
.
Заметим, что при нахождении функции  константа С должна присутствовать обязательно. Теперь можно записать общее решение исходного дифференциального уравнения
константа С должна присутствовать обязательно. Теперь можно записать общее решение исходного дифференциального уравнения  .
.
При каждом конкретном значении С получается конкретная функция, которая является решением дифференциального уравнения. А поскольку  , то получается, что данное дифференциальное уравнение имеет бесконечно много решений. На Рис. 1 изображены графики пяти частных решений при
, то получается, что данное дифференциальное уравнение имеет бесконечно много решений. На Рис. 1 изображены графики пяти частных решений при  .
.

| С=2 |
| С=1 |
| С=0 |
| С=-1 |
| С=-2 |
| Рис. 1 |
| Рис. 1 |
По условию задачи нам нужно найти решение, удовлетворяющее начальным данным  . Геометрически это означает, что график этого решения должен проходить через точку
. Геометрически это означает, что график этого решения должен проходить через точку  . Чтобы найти это решение аналитически (т.е. его формулу), нужно в формулу общего решения подставить вместо буквы у число (-3), а вместо буквы х число 1. В результате получится одно уравнение с одним неизвестным С. В нашем примере это уравнение имеет вид:
. Чтобы найти это решение аналитически (т.е. его формулу), нужно в формулу общего решения подставить вместо буквы у число (-3), а вместо буквы х число 1. В результате получится одно уравнение с одним неизвестным С. В нашем примере это уравнение имеет вид:  . Теперь нужно найденное значение С подставить в формулу общего решения:
. Теперь нужно найденное значение С подставить в формулу общего решения:
 .
.
График этого решения на Рис. 2 нарисован жирной линией.

|
Ответ. Решение задачи Коши – это функция  .
.
Date: 2016-02-19; view: 440; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |
