Это фрагмент таблицы, для наглядности

Вопрос 31 Табулирование распределений.

Вопрос 32 Зависимые и независимые случайные величины.

Две случайные величины считаются независимыми, если возможные значения и закон распределения каждой из них один и тот же при любом выборе допустимых значений другой. В противном случае они называются зависимыми. Несколько случайных величин называются взаимно независимыми, если возможные значения и законы распределения любой из них не зависят от того, какие возможные значения приняли остальные случайные величины.

Вопрос 33 Математическое ожидание случайной величины. Свойства математического ожидания.

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности.

Случайной называют величину, которая в результате испытания примет одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Математическое ожидание Мx (или М(x)) случайной величины x определяется формулой Мx=Σ _i=1ⁿ x _i p _i, где x - случайная величина, р – вероятность исхода, х – значение величины.

Свойства математического ожидания: 1. Если случайная величина x принимает одно и то же значение при всех исходах случайного эксперимента, то есть x º С, то её математическое ожидание равно С (Математическое ожидание постоянной величины равно самой постоянной). 2. Если Мx = а, и k – константа, то М(kx) = kа (Постоянный множитель можно выносить за знак математического ожидания.). 3. Если Мx = а, и k – константа, то М(k + x) = k + а (математическое ожидание суммы случайной величины и числа равно сумме этого числа и математического ожидания случайной величины). 4. М(x + h) = Mx + Mh (Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых). 5. М(xh) = Мx×Мh (Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий)

Вопрос 34 Дисперсия случайной величины. Свойства дисперсии.

Дисперсия случайной величины - мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений. Обозначается DX. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения. Отклонением называют разность между случайной величиной и ее математическим ожиданием (Х – М[Х]). Средним квадратичным отклонением называется квадратный корень из дисперсии. DX=E[(X-EX) ² ], где E – математическое ожидание; DX=E[X ² ]-(EX) ², где E – математическое ожидание; σx=σ[x]=√D[X], где ơ[x] – среднее квадратичное отклонение.

Свойства дисперсии: 1. Дисперсия постоянной величины с равна нулю. 2. При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется (D [ X + c ] = D [ X ]). 3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с². 4. Дисперсия всегда неотрицательна (Dx≥0). 5. Дисперсия обращается в нуль лишь для вырожденного распределения: (если Dx=0, то x=const). 6. Если x и n независимы, то дисперсия их суммы равна сумме их дисперсий: В(x+n)=Dx+Dn.

Вопрос 35 Моменты случайной величины, ассиметрия, эксцесс.

Момент случайной величины - числовая характеристика распределения данной случайной величины. Если дана случайная величина X то: 1. k-м начальным моментом случайной величины Х называется величина V _k =E=[X ^k ], если математическое ожидание E[*] в правой части этого равенства определено; 2. 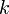-м центра́льным моментом случайной величины X называется величина u _k =E[(X-EX) ^k ], 3. k-м абсолю́тным и k-м центральным абсолютным моментами случайной величины Х называется соответственно величины V _k =E[|X| ^k ] и u _k =E[|X-EX| ^k ], 4. k-м факториальным моментом случайной величины Х называется величина u _k =E[X(X-1)..(X-k+1)], если математическое ожидание в правой части этого равенства определено. Геометрический смысл некоторых моментов: 1. V ₁ равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой. 2. u₂ равняется дисперсии распределения (u₂=σ ²) и показывает разброс распределения вокруг среднего значения. 3. u ₃, будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение называется коэффициентом асимметрии. 4. u₄ контролирует, насколько ярко выражена вершина распределения в окрестности среднего.

Коэффициент асимметрии - величина, характеризующая асимметрию распределения данной случайной величины. Пусть задана случайная величина Х, такая что E|X| ³ <∞. Пусть u ₃ обозначает третий центральный момент: u ₃ =E[(X-EX) ³ ], а σ=√D[X] – стандартное отклонение Х. Тогда коэффициент асимметрии задаётся формулой:ᵞ ₁ =u ₃ \σ ³. Коэффициент эксцесса - мера остроты пика распределения случайной величины. Пусть задана случайная величина Х, такая что Е|X| ⁴ <∞. Пусть u ₄ обозначает четвёртый центральный момент: u ₄ =Е[(X-EX) ⁴ ], а σ=√D[X] – стандартное отклонение Х. Тогда коэффициент эксцесса задаётся формулой: ᵞ ₂ = u ₄ \σ ⁴ -3.