Способы задания функции

Существует несколько способов задания функции.

Табличный. Используется тогда, когда область определения состоит из

конечного множества чисел. Тогда для задания функции проще всего указать

таблицу, содержащую значения аргумента и соответствующие значения

функции. Например, таблица логарифмов. Другим примером могут быть

таблицы, содержащие данные о числе жителей, населяющих земной шар в

отдельные годы, расписания движения поездов и т.п.

Аналитический. При аналитическом способе задания функция может

быть задана явно, когда дано выражение у через x, т.е. формула имеет вид

y  f (x); неявно, когда х и у связаны между собой уравнением вида F (x, y)  0;

параметрически, когда соответствующие друг другу значения х и у выражены

через третью переменную величину t, называемую параметром.

Логический. Если функция описывается правилом ее составления,

например, функция Дирихле: f (x) = 1, если x – рациональное; f (x) = 0, если x –

иррациональное.

Графический. Состоит в изображении графика функции – множества

точек (x, y) плоскости, абсциссы которых есть значения аргумента

функции (в декартовой прямоугольной системе координат)

называют геометрическое место точек, абсциссы которых являются значениями

Лекция №2 «Функции и способы их задания»

независимой переменной, а ординаты – соответствующими значениями

функции.

Преобразования графиков функций.

Покажем, как из графика функции y  f (x) можно получить графики

функций вида y  Af (ax  b)  B, где A, В, a, b – некоторые действительные

числа.

1. График функции y  f (x)  b получается из графика функции y  f (x)

параллельным переносом.

Если b  0, то перенос совершается параллельно оси ординат на

расстояние b вверх, а если b  0, то вниз на расстояние | b |. На рис.

изображены графики функций y  x 2 (пунктирной линией) и y  x 2 1

(сплошной линией).

2. График функции y  f (x  a) также получается из графика функции

y  f (x) параллельным переносом.

Если a  0, то график переносится параллельно оси абсцисс влево на

расстояние а, а если a  0, то вправо на расстояние | a |. На рис. изображены

графики функций y  x 2 (пунктирной линией) и y  (x 1)2 (сплошной

линией).

3. График функции y  Af (x), где A  0, получается из графика

функции y  f (x) растяжением или сжатием вдоль оси ординат.

Если A 1, то график функции растягивается вдоль оси О у в A раз, а

если 0  A 1, то сжимается в 1 A раз. На рис. изображены графики функций

y  sin x (пунктирной линией) и y  2sin x (сплошной линией).

4. График функции y  f (ax), где a  0, получается из графика функции

y  f (x) сжатием к оси ординат или растяжением вдоль оси абсцисс.

Лекция №2 «Функции и способы их задания»

График функции y  f (ax) есть график y  f (x), сжатый (при a 1) в а

раз или растянутый (при 0  a 1) вдоль оси Ох. На рис. изображены графики

функций y  sin x (пунктирной линией) и y  sin 2 x (сплошной линией).

5. График функции y   f (x) получают из графика функции y  f (x)

зеркальным отражением относительно оси абсцисс.

На рис. изображены графики функций y  x 2 (пунктирной линией) и

y   x 2 (сплошной линией).

6. График функции y  f ( x) получается из графика функции y  f (x)

зеркальным отражением относительно оси ординат.

На рис. изображены графики функций y  ax, где a  0 (пунктирной

линией) и y  a  x (сплошной линией).

21) Обратная функция

Обратная функция

Функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = φ (y), является обратной по отношению к данной функции у = f (x). Например, О. ф. для у = ax + b (а≠0) является х = (у—b)/a, О. ф. для у = е^х является х = ln у и т.д. Если х = φ(y) есть О. ф. по отношению к у = f (x), то и у = f (x) есть О. ф. по отношению к х = φ(y). Областью определения О. ф. является область значений данной функции, а областью значений О. ф.— область определения данной. Графики двух взаимно обратных функций у = f (x) и у = φ (x) (где независимое переменное обозначено одной и той же буквой х), как, например, у = ax + b и у = (х—b)/a, у = е^х и у = ln х, симметричны по отношению к биссектрисе у = х первого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции х² и 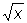у = f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). О. ф. по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна

Сложная функция:

Пример 1. Дана функция f (x) = 3 x ² – 4. Найти:

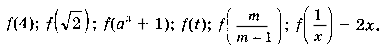
Решение: f (4) = 3•4² – 4 = 48 – 4 = 44;

f (a ³ + 1) = 3(a ³ + 1)² – 4 = 3(a ⁶ + 2 a ³ + 1) – 4 =

= 3 a ⁶ + 6 a ³ – 1;

f (t) = 3 t ² – 4;

Пример 2. Найти функцию f (x), если f (x + 1) = x ² + 2 x + 2.

Решение. Пусть x + 1 = a, тогда x = a – 1; f (a) = (a – 1)² + 2(a – 1) + 2 = a ² – 2 a + 1 + 2 a – 2 + 2 = a ² + 1.

Ответ: f (x) = x ² + 1.

Пример 3. F (2 x – 1) = 4 x – 7; F (g (x)) = x ³. Найти g (x).

Решение. Пусть 2 x – 1 = a, тогда

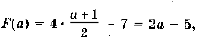
т. е. F (x) = 2 x – 5. Значит,

F (g (x)) = 2 g (x) – 5. 2 g (x) – 5 = x ³.

Ответ: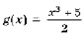

Сложная функция – функция от функции. Если z – функция от у, т.е. z (y), а у, в свою очередь, – функция от х, т.е. у (х), то функция f (x) = z (y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z (y).

Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:

.

Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f ₁(y ₁), y ₁ = f ₂(y ₂), …, y_{n -1} = f_n (x), то

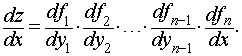
Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k x, где k - постоянная величина (коэффициент пропорциональности). График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол , тангенс которого равен k: tan = k (рис.8). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.
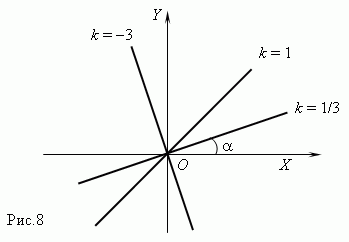
	Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:   A x + B y = C,   где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
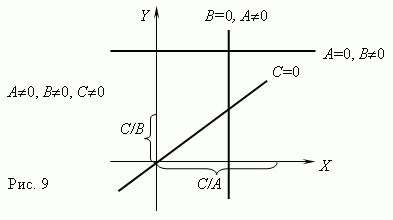
	Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x, где k - постоянная величина. График обратной пропорциональности – гипербола (рис.10). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конусаплоскостью (о конических сечениях см. раздел «Конус» в главе «Стереометрия»). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy= k.     Основные характеристики и свойства гиперболы: - область определения функции: x 0, область значений: y 0; - функция монотонная (убывающая) при x < 0 и при x > 0, но не монотонная в целом из-за точки разрыва x = 0 (подумайте, почему?); - функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая; - нулей функция не имеет.
	Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a 0. В простейшем случае: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы. 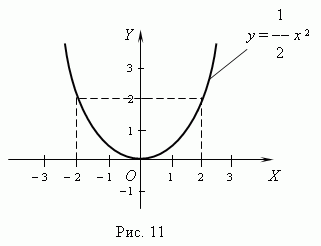  График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в начале координат, а в точке с координатами: 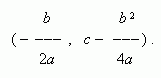Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x 2 и дискриминанта D = b 2 – 4 ac. Эти свойства следуют из анализа корней квадратного уравнения (см. соответствующий раздел в главе «Алгебра»). Все возможные различные случаи для квадратной параболы показаны на рис.12.

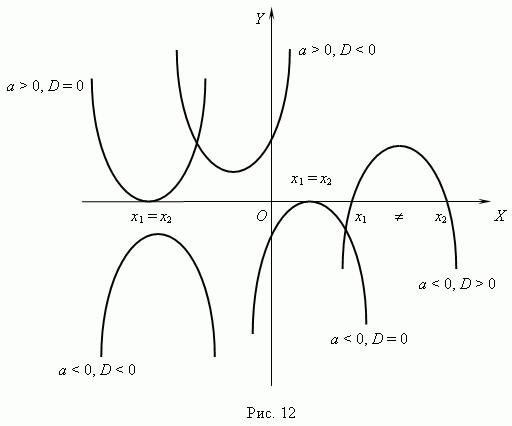
Изобразите, пожалуйста, квадратную параболу для случая a > 0, D > 0.

Основные характеристики и свойства квадратной параболы:

- область определения функции: - < x < + 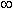(т.e. x 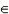R), а область

значений: … (ответьте, пожалуйста, на этот вопрос сами!);

- функция в целом не монотонна, но справа или слева от вершины

ведёт себя, как монотонная;

- функция неограниченная, всюду непрерывная, чётная при b = c = 0,

и непериодическая;

- при D < 0 не имеет нулей. (А что при D 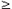0?).

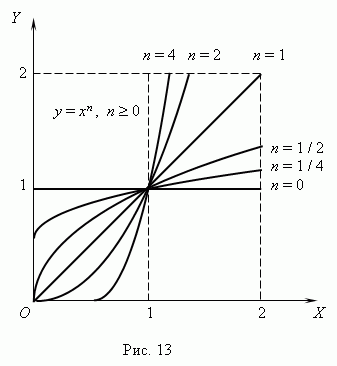
5.

Степенная функция. Это функция: y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 - квадратную параболу; при n = -1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степеннойфункции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, при n = 0 степенная функция превращается в постоянную величину: y = a, т.e. её график - прямая линия, параллельная оси Х, исключая начало координат (поясните, пожалуйста, почему?).Все эти случаи (при a = 1) показаны на рис.13 (n 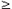0) и рис.14 (n < 0). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции: 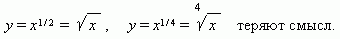 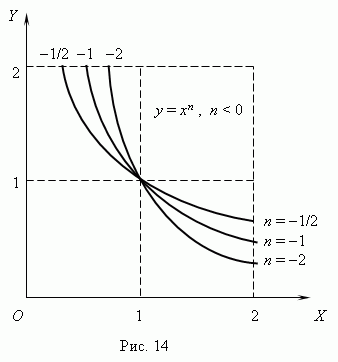   Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3. 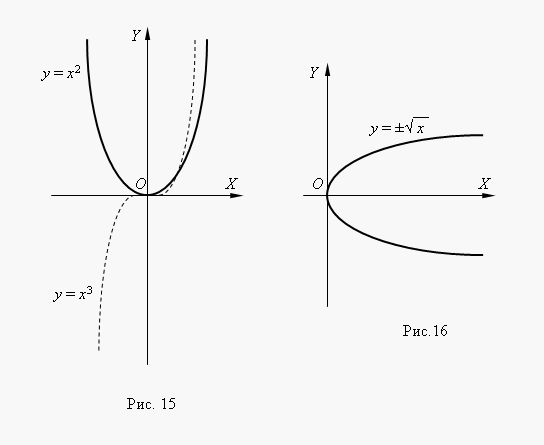При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой. На рис.16 представлена функция 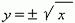. Эта функция является обратной к квадратной параболе y = x 2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.

6.

Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте,пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает. 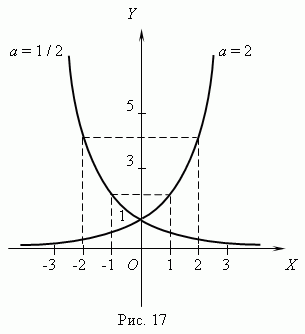Основные характеристики и свойства показательной функции: - область определения функции: - < x < + (т.e. 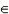x R); область значений: y > 0; - функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - нулей функция не имеет.

7.

Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график (рис.18) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.

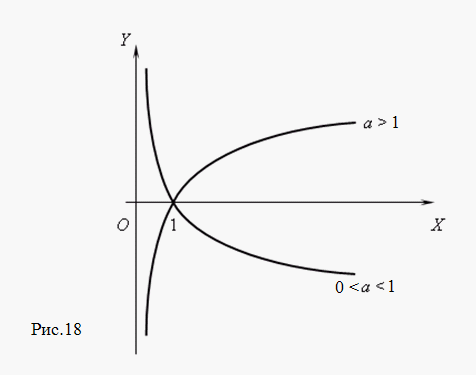
22)Числовая последовательность:

Date: 2015-06-05; view: 1089; Нарушение авторских прав