Совпадения бесконечности

Суждение, попав в логический круг, начинает вертеться в нем – значения не фиксируется, и меняется бесконечное число раз по циклу: “Суждение истинно значит ложно, суждение ложно значит истинно”.

Так же, до бесконечности, продолжается построение “монстра”.

Бесконечность присутствует как в изменении значений парадоксального высказывания, так и в итерациях “монстров”.

Бесконечность сводит с ума борцов с монстрами, являясь символом нелогичности и иррациональности.

Концептуальные совпадения

Есть несколько научных и философских концепций, обращающихся одновременно и к математическим монстрам, и к логическим парадоксам.

Во-первых, это теория хаоса и концепция сложности (complexity), синергетическая парадигма, которые приводят парадоксы в качестве результата "линейного" мышления. «Монстры» в этих концепциях - формы нового, "нелинейного" мира.

Во-вторых, это концепция автопоэзиса, бурно развиваемая сейчас философами, биологами и социологами, основателями которой считаются чилийские биологи и эпистемологи Умберто Матурана и Франциско Варела[4]. Франциско Варела в своих работах приводил монстры и парадоксы в качестве моделей саморазвивающихся, самодостраивающихся автопоэтических систем[5].

Многие статьи У. Матураны и Ф. Варелы присутствуют в ИНТЕРНЕТ. В качестве отправной точки можно сходить на сервер www.synergetic.ru, где присутствуют обзоры и библиография работ.

Наша задача состоит в том, чтобы выстроить совпадения математических "монстров" и логических парадоксов на концептуальном поле фрактальной геометрии.

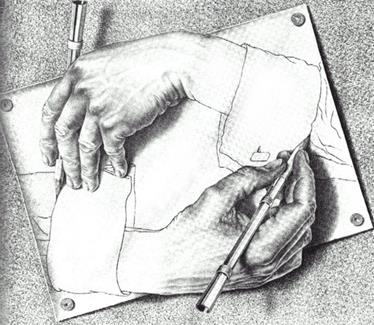
Рис 1.3.15 Иллюстрация бесконечного самодостраивания и цикличности: метафора автопоэзиса. М. Эшер. Руки.

1.4 Исторический очерк фрактальной геометрии

…(и что этот образ? не явь и не сон,

не заболеванье и не исцеленье,

а с криком летящая над колесом

мгновенная ласточка одушевленья)

тогда он и скажет себе: - Чудеса!

Не я ли раздвинул тяжелые вещи,

чтоб это дышало и было как сад,

как музыка около смысла и речи,

и было псалтырью, толкующей мне

о том, что никто, как она, не свободен, -

словами, которых не ищут в уме

делами, которых нигде не находят...

Ольга Седакова "Последний читатель"

"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Число различных масштабов длин в структурах всегда бесконечно.

Существование этих структур бросает нам вызов в виде трудной задачи изучения тех форм, которые Евклид отбросил как бесформенные - задачи исследования морфологии аморфного. Математики, однако, пренебрегли этим вызовом и предпочли все больше и больше отдаляться от природы, изобретая теории, которые не соответствуют ничему из того, что можно увидеть или почувствовать."

Этими, ставшими уже популярными, словами американский математик Бенуа Мандельброт начинает свой всемирно известный бестселлер “The Fractal Geometry of Nature”[6].

Фрактальная геометрия, по Мандельброту это и есть настоящая геометрия природы, отличающаяся от традиционных геометрий, уводящих человека в царство безжизненных абстракций. Природа аморфна и причудлива.

Фрактал - форма природного хаоса, форма аморфного, форма бесформенного, приближающая взгляд и ум человека к природе.

Термин "фрактал" предложен Мандельбротом. Вот что пишет он сам по этому поводу в разделе “Фрактал” и другие неологизмы” во введении к своей книге “Фрактальная геометрия природы”[7]:

"Я создал термин фрактал от латинского прилагательного fractus. Соответствующий латинский глагол frangere означает "разрывать, прерывать": создавать нерегулярные фрагменты. Это, следовательно, имеет (подходящее для нас!) значение дополнительное к термину "фрагментированный" (как и к фракция (fraction), рефракция (refraction)), fractus также "нерегулярный", оба значения сохраняются в термине fragment.

Правильнее поизносить - frac'tal - с ударением таким же, как и в слове fraction.

Сочетание “фрактальное множество” (fractal set) будет определена строго, но сочетание “природный фрактал” (nature fractal) будет подано свободно - для определения природных примеров, которые полезно репрезентировать с помощью фрактальных множеств. Например, броуновская кривая - это фрактальное множество, а физическое броуновское движение - это природный фрактал.

(Поскольку алгебра происходит от Арабского jabara = “связывающего вместе”, фрактал и алгебра стоят в этимологических оппозициях!)

Обычно, в моих путешествиях по вновь открытой или заново определенной территории, я часто перемещался под влиянием права на присваивание имени поворотным пунктам этой территории. Как правило, тщательно созданный неологизм представляется более лучшим, чем добавление новый морщина к уже затасканному термину.”

Мандельброт рассматривает математические аналоги природных форм и уточняет представление о фракталах – особых геометрических множествах, форма которых принципиально отличается от традиционных геометрических форм типа точки, линии и плоскости.

В качестве примера фракталов Мандельброт рассмотрел множества Жюлиа Мандельброта на комплексной плоскости.

В основе построения этих множеств лежит рекуррентная процедура - процесс итерации z®f(z,c), где z -комплексная переменная, c - комплексная константа, f - нелинейная функция.

Если x и y - координаты плоскости, то переменная z=x+iy, константа c=p+iq, а, например, нелинейную функцию можно выбрать такую: f(z,c)=z*z+c.

Тогда если c=0, то все точки z делятся на три класса:

1.|z|<1 => аттрактор точки z - это точка (0,0),

2.|z|=1 => точка z останется на окружности радиуса 1,

3.|z|>1 => аттрактор точки z - бесконечность,

Если c - не нуль, то возникает аттрактор, отличный от нуля.

Аттракторы - это центры притяжения, которые ведут борьбу за влияние на плоскости; любая начальная точка либо в течение процесса приходит к тому или иному аттрактору, либо лежит на границе и не может принять определенного решения. С изменениями параметров меняются и области влияния аттракторов, а вместе с ними и границы.

Множества Жюлиа и Мандельброта строятся рекурсивно при помощи различных функций F и G, позволяющих перейти от k-той точки на плоскости к (k+1)-ой точке по следующему закону:

x(k+1)=F(x(k), y(k),p),

y(k+1)=G(x(k), y(k),q),

где p и q - параметры, которые считаются постоянными в течение каждой итерации (x(0),y(0))->(x(1),y(1))->...->(x(k),y(k))->... В качестве функций F и G можно рассматривать различные нелинейные функции. Если плоскость, состоящая из всех пар (x,y), рассматривается при фиксированных p и q, то получаются так называемые множества Жюлиа. Если, напротив, фиксируется начальная пара значений (x,y) и прослеживается ее судьба при различных значениях параметров p и q, то получаются изображения, называемые множествами Мандельброта.

Вот что писал великий английский физик и математик Роджер Пенроуз по поводу фрактального множества Мандельброта:

“Доводилось ли вам когда-нибудь видеть картины, нарисованные компьютером, - объекты, известные под названием множеств Мандельброта? Впечатление такое, как будто вы отправляетесь в путешествие в какой-то далекий мир. Вы включаете свое чувствительное устройство, видите невероятно сложную конфигурацию с множеством всевозможных деталей и пытаетесь понять, что это такое. Вы можете вообразить, что перед вами какой-то необыкновенный ландшафт или, быть может, живое существо, облепленное со всех сторон крохотными детенышами, очень похожими на породившее их создание, но всё же несколько отличающееся от него. Весьма искусная и впечатляющая картина!

И всё же, даже глядя на уравнения, никто не имел ни малейшего представления о том, что они могут порождать структуру такого типа. А ведь эти ландшафты - не плод чьего-то разыгравшегося воображения: все видят одну и ту же картину.

Вы исследуете нечто с помощью компьютера, но это ничем не отличается от исследования, проводимого с помощью обычной экспериментальной техники.”

Мандельброт демонстрирует методологию описания множеств, полученных с помощью рекуррентных процедур.

В качестве качественного инварианта описания он применяет понятие самоподобия, подразумевающее подобие фрагмента множества, полученного бесконечной рекуррентной процедурой, всему множеству.

Рис. 1.4.1 Бенуа Мандельброт (род. 1924)

Автор термина "фрактал" и основоположник фрактальной геометрии.

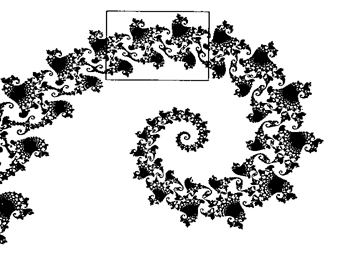
а) б) в) г) д) е) Рис 1.4.2 а)-е) Фрагменты множества Мандельброта при различных масштабах. Фрагмент в рамке показан на следующем (по буквенному обозначению) рисунке. Фрагмент в е) напоминает по форме а).

Для количественного описания фрактальных множеств Мандельброт предложил использовать понятие размерности фрактального множества.

В обычном понимании размерность геометрического множества есть число измерений, с помощью которых можно задать положение точки на геометрическом объекте.

В свое время бурные дискуссии вызвал переход в “многомерие” - от плоскостей с размерностью два и евклидовых пространств с размерностью три, к менее представляемым n-мерным абстракциям. Достаточно сложно себе представить четырех, пяти или шестимерное пространство.

Сходная ситуация, на наш взгляд, складывается и в связи с освоением концепции фрактала.

Переход от «линейного мышления» к «фрактальному» сопряжен с введением новых интерпретаций размерности - числа измерений предметов.

Фрактальная геометрия заставляет мыслить в понятиях “дробномерия” - дробных измерений, или даже “дробномирия”.

Вот что пишут Ю.А.Данилов и Б.Б.Кадомцев в известной статье "Что такое синергетика?"[8]:

Мандельброт предложил использовать в качестве меры «нерегулярности» (изрезанности, извилистости и т. п.) определение размерности, предложенное Безиковичем и Хаусдорфом. Фракталь (неологизм Мандельброта) - это геометрический объект с дробной размерностью Безиковича-Хаусдорфа...

...Размерность Безиковича-Хаусдорфа всегда не меньше евклидовой и совпадает с последней для регулярных геометрических объектов (для кривых, поверхностей и тел, изучаемых в современном учебнике евклидовой геометрии). Разность между размерностью Безиковича-Хаусдорфа и евклидовой - «избыток размерности» - может служить мерой отличия геометрических образов от регулярных. Например, плоская траектория броуновской частицы имеет размерность но Безиковичу-Хаусдорфу больше 1, но меньше 2: эта траектория уже не обычная гладкая кривая, но еще не плоская фигура....

...Под фракталом, подразумевался некий сильно изрезанный, геометрический объект, который являлся, например уже не точкой, но еще не гладкой линией, или уже не линией, но еще не плоскостью.”

Мандельброт специально нашел такое определение размерности (размерности по Хаусдорфу и Безиковичу), которое бы в частном случае соответствовало нашим представлениям о классических целых размерностях, а в общем случае позволяло вводить и измерять фрактальные предметы.

Для уточнения понятия размерности рассмотрим множество S точек в некотором евклидовом пространстве.

Будем покрывать это множество по очереди отрезками прямой, квадратами, кубами. Для этого выберем функцию покрытия h(d) = g(d)dd, которая при d=1 соответствует прямолинейным отрезкам, при d=2 квадратам, при d=3 - кубам. g - это геометрический коэффициент равный в нашем случае единице.

Рассмотрим меру множества Md=Sh(d). Мера – это общее понятие для таких понятий как длина, площадь и объем, которая работает "в зазорах" между этими понятиями.

При d®0 мера Mdравна нулю или бесконечности в зависимости от выбора d-размерности меры. Например, при покрытии фрагмента плоскости отрезками (d=1) мера равна бесконечности так как длина плоскости бесконечна - поверхность нельзя покрыть конечным числом отрезков, чья длина стремится к нулю. При покрытии фрагмента плоскости кубиками (d=3), мера стремится к нулю - объем плоскости равен нулю. Однако, при d=2 мера плоскости стремится к конечной величине. Этой мерой служит площадь исследуемого нами фрагмента плоскости.

При покрытии фигуры Коха (рис.1.1.1) отрезками (d=1), мера (длина фигуры) стремится к бесконечности. При покрытии фигуры Коха квадратами (d=2) мера (площадь фигуры) стремится к нулю. Этот факт дает основание предположить, что между d=1 и d=2 должно существовать значение d, при котором мера меняет свое значение с нуля на бесконечность.

Размерность Хаусдорфа-Безиковича D множества S есть критическая размерность, при которой мера Mdменяет своё значение с нуля на бесконечность:

Md=Sg(d)dd 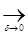0 при d>D; Md=Sg(d)dd 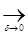¥ при d<D.

В случае с плоскостью, размерность Хаусдорфа-Безиковича равна двум. В случае фигуры Коха эта размерность не является целой и является фрактальной. Мера фигуры Коха не является длиной и площадью, а находится между ними.

Для определения размерности сложной фигуры на евклидовой плоскости (береговой линии, кластера), ее покрывают набором квадратов со стороной l ®0, и при различных l подсчитывают число квадратов N(l). Далее ищется степенная функция меры таким образом, чтобы она была конечной при каком-то показателе степени. Для этого в двойных логарифмических координатах строится зависимость числа квадратов, покрывших фигуру, от длины сторон этих квадратов. Получается график, похожий на график зависимости длины береговой линии от функции выбранного шага (рис. 1.5.2). По углу наклона этого графика определяется фрактальная размерность.

Размерности можно вводить и по-другому. Будем покрывать изучаемое множество в p -мерном пространстве кубиками с ребром e. Кубику с номером i сопоставим вероятность P i, с которой в него попадают точки множества. Далее можно ввести набор величин D q называемых обобщенными размерностями, по формуле:

D q = ,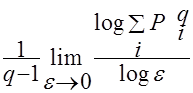

где суммирование ведется по всем кубикам покрытия.

При разных q возникают разные виды размерностей, характеризующих исследуемое множество - степень упорядоченности точек в пространстве.

Теория размерности – область математики, активно разрабатываемая в работах А. Н. Колмогорова, А. Реньи, Ф. Хаусдорфа.

1.4.3 Феликс Хаусдорф (1868 - 1942)

Автор оригинальных трудов по теории множеств, топологии, функциональному анализу. Предложил понятие меры и размерности, которое использовал Мандельброт для количественного описания фракталов. В 1942 году покончил жизнь самоубийством, узнав о предстоящей отправке своей семьи в гитлеровский концлагерь.

Рис. 1.4.4 Андрей Николаевич Колмогоров (1903 - 1987)

Великий советский математик. Получил фундаментальные результаты в теории множеств, теории меры, используемые в хаотической и фрактальной динамике.

Рис. 1.4.5 Альфред Реньи (1921 - 1970)

Внес большой вклад в теорию размерностей и теорию множеств. Во фрактальной геометрии и мультифрактальном анализе активно используется понятие обобщенной размерности, введенное Альфредом Реньи.