Экономическая интерпретация множителей Лагранжа

В некоторых задачах Множители Лагранжа допускает экономическое толкование.

Представим себе, что условие выражает собой ограничение на дефицит ресурса, где постоянная величина b характеризует наличие некоторого ресурса. Будем толковать функцию как доход получаемый некоторым предприятием, при использовании ресурса.

С экономической точки зрения в этом случае множители Лагранжа интерпретируются как неявные (теневые) цены ресурсов, определяемых ограничениями. (Теневые (неявные) цены определяют приращение максимального дохода при использовании дополнительной единицы некоторого ресурса). Оптимальные значения множителей Лагранжа играет важную роль в анализе чувствительности решений. Для того чтобы пояснить эту интерпретационную схему, рассмотрим сложную оптимизационную задачу с двумя переменными и одним ограничением в виде равенства:

(2.45)

при ограничении

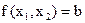(2.46)

Функция Лагранжа имеет вид

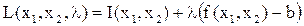
Необходимые условия оптимума следующие:

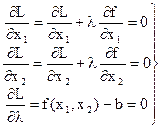. (2.47)

Из этой системы уравнений находим оптимальные значения x₁,х₂, λ.

Пусть λ* – оптимальное значение множителя Лагранжа, а 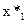, 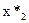– оптимальное решение задачи. Далее, пусть максимум функции 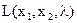при λ = λ* достигается в точке 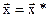, причём 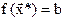и 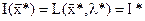. Очевидно, что оптимальные значения 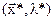связаны функциональной зависимостью с величиной b, задающей границу наличия дефицитного ресурса.

Изменения I* (оптимального значения I), обусловленные изменениями b, описываются частной производной 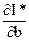. По правилу дифференцирования сложной функции имеем:

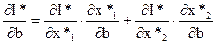(2.48)

Дифференцируя обе части ограничения f﴾x₁, х₂) – b=0, получаем

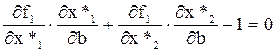(2.49)

Умножим обе части равенства (2.49) на λ* и суммируем с равенством (2.48):

(2.50)

Так как 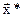и λ* удовлетворяют уравнениям (2.47), равенство (2.20) приводится к виду

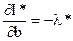(2.51)

Таким образом, из формулы (2.51) следует скорость изменения оптимального значения I, вызываемого изменением b, с точностью до знака равна оптимальному значению множителя Лагранжа (на знак самого множителя Лагранжа λ никаких требований не накладывается). Другими словами, величина изменения оптимального значения целевой функции (теневая цена), обусловленного единичным увеличением правой части ограничения, задаётся множителем Лагранжа. В зависимости от знака λ* значение I* при изменении b могут увеличиваться или уменьшатся.

В случае когда рассматривается оптимизационная задача с m ограничениями и n переменными (m<n):

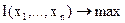
при ограничениях

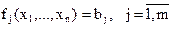
пользуясь аналогичной схемой рассуждений, можно показать, что

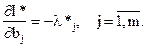
Date: 2015-05-23; view: 3415; Нарушение авторских прав