Методические указания 3 page

Найдём, подставив вместо 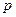в выражении (числитель) (2.48) первый корень характеристического уравнения (2.16):

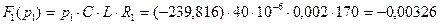(2.52)

В выражение (2.50) подставим первый корень характеристического уравнения (2.16) и получим:

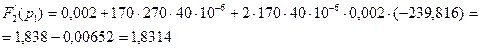(2.53)

Найдем, 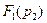подставив вместо 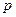в выражении (числитель) (2.48) второй корень характеристического уравнения (2.17):

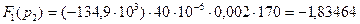(2.54)

В выражение (2.50) подставим, второй корень характеристического уравнения (2.17) и получим:

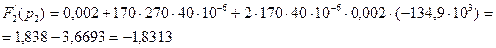(2.55)

Подставляем найденные значения (2.52), (2.53), (2.54) и (2.65) в выражение (2.51):

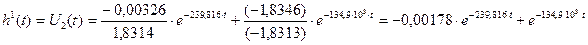
(2.56)

Расчет классическим методом (2.43) и операторным методом (2.56) практически совпадают, с учетом допустимой погрешности, можно сделать вывод, что переходная характеристика найдена, верно.

2.3 Расчет переходной характеристики цепи классическим методом при условии, что корни характеристического уравнения будут комплексно- сопряженные

Для того, что бы показать расчет переходной характеристики в случае, если корни характеристического уравнения будут комплексно – сопряженные, возьмем другую схему четырехполюсника с другими параметрами заданной цепи.

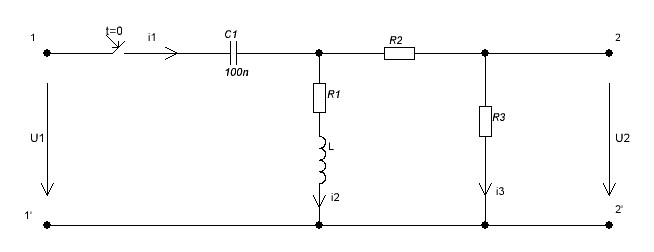
Рисунок 2.4 – Рассчитываемая цепь до коммутации

Параметры заданного четырехполюсника:

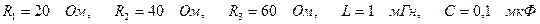
Производим анализ цепи до коммутации. В результате этого анализа определяю токи во всех ветвях электрической цепи и напряжение на ёмкости в момент времени, непосредственно предшествующий коммутации (t=0_).

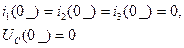(2.57)

По законам коммутации:

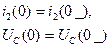(2.58)

Независимые начальные условия равны:

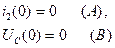(2.59)

Составляем систему дифференциальных уравнений на основании законов Кирхгофа, описывающую процесс в цепи после коммутации (t≥0):

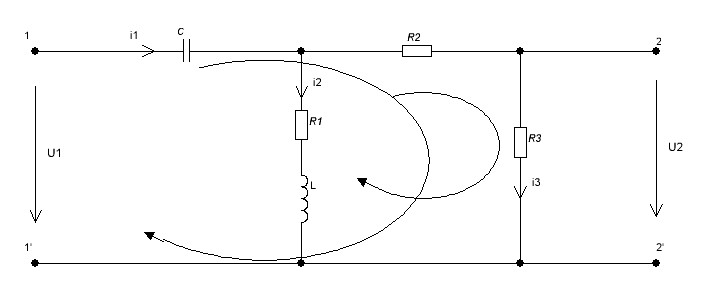
Рисунок 2.5 – Рассчитываемая цепь после коммутации

Направления обхода контура выбираем произвольно (рисунок 2.5), .

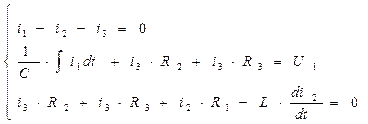(2.60)

Ток 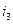представим в виде суммы установившегося и свободного режима цепи:

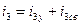(2.61)

Определим ток 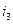в установившемся режиме цепи после коммутации. Так как на входе цепи включена ёмкость, то в установившемся режиме работы цепи все токи будут равны нулю.

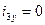(2.62)

Определим свободную составляющую тока 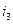для этого необходимо, получить характеристическое уравнение цепи после коммутации. Наиболее простой способ составления характеристического уравнения – метод входного сопротивления.

Запишем характеристическое уравнение заданного четырехполюсника (рисунок 2.5):

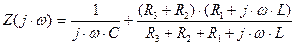(2.63)

Заменяем в выражении (2.63) 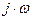на 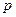и приравниваем его к нулю:

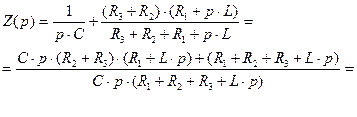(2.64)

Приравняем к нулю числитель выражения (2.64):

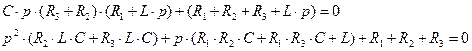(2.65)

Уравнение (2.65) является характеристическим уравнением цепи. Характеристическое уравнение цепи можно составить другим способом. Запишем определитель исходной системы уравнений и приравниваем его к нулю:

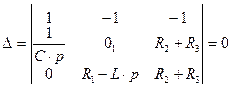(2.66)

Выполнив необходимые преобразования, получим:

(2.67)

Приравняв к нулю числитель выражения (2.67), получим:

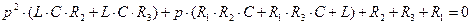(2.68)

Полученное квадратное уравнение (2.67) полностью совпадает с квадратным уравнением (2.65).Обоими способами были получены абсолютно идентичные уравнения и соответственно можно сделать вывод, что расчеты выполнены правильно.

Подставив числовые значения параметров цепи в характеристическое уравнение (2.68), вычислим его корни:

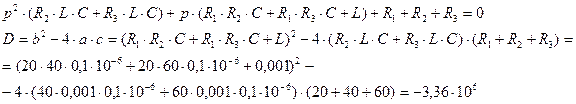
(2.69)

Дискриминант получился 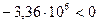, находим корни:

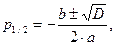(2.70)

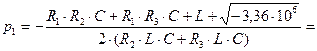
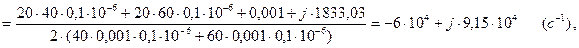
(2.71)

(2.72)

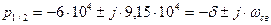(2.73)

Корни характеристического уравнения комплексно – сопряженные, поэтому характер переходного процесса – колебательный, следовательно свободная составляющая тока 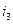будет иметь вид:

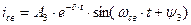(2.74)

где 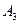, 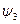- постоянные интегрирования.

Для расчета постоянных интегрирования определим зависимые начальные условия. Запишем исходную систему уравнений (2.60) для :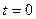

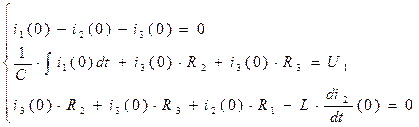(2.75)

Из независимых начальных условий ,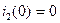

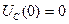
Из второго уравнения системы уравнений (2.75) определяем :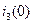

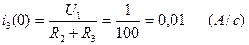(2.76)

Из третьего уравнения системы уравнений (2.75) определяем :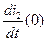

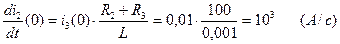(2.77)

Подставляем значений второго тока 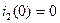и третьего тока 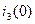(2.76) в первое уравнение системы уравнений (2.75) и получаем значение первого тока в нулевой момент времени :

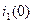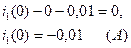(2.78)

Продифференцируем первое и второе уравнение системы уравнений (2.75) и запишем их для :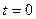

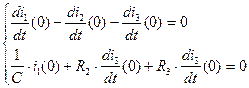(2.79)

Из второго уравнения системы уравнений (2.79) находим 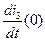, подставляя известные значения конденсатора 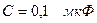, значения сопротивлений и значения первого тока в нулевой момент времени 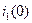(2.78):

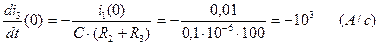(2.80)

Определим постоянные интегрирования 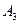и 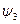для определения свободной составляющей третьего тока (2.74) Так как установившаяся составляющая тока третьего равна нулю, то ток в цепи будет определяться только свободной составляющей:

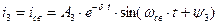(2.81)

Продифференцируем уравнение для тока 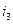(2.81) и запишем их для :

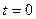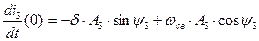(2.82)

Запишем уравнение (2.81) для :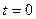

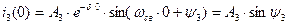(2.83)

Из двух уравнений (2.82) и (2.83) составим одну систему уравнений:

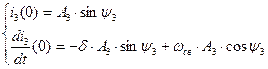(2.84)

Решаем систему уравнений (2.84), подставляя известные численные значения 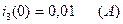(2.76), 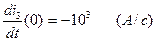(2.80), 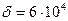(2.73), 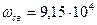(2.73) и находим постоянные интегрирования 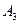и :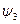

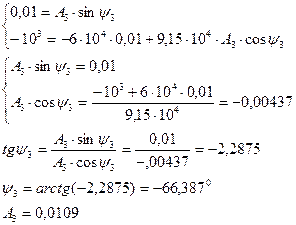(2.85)

Подставляем полученные постоянные интегрирования 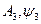(2.85) в выражения для искомого тока третьего (2.81):

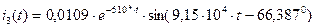(2.86)

Таким образом, переходная характеристика заданного четырехполюсника имеет вид:

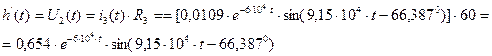(2.87)

2.4 Расчет переходной характеристики операторным методом

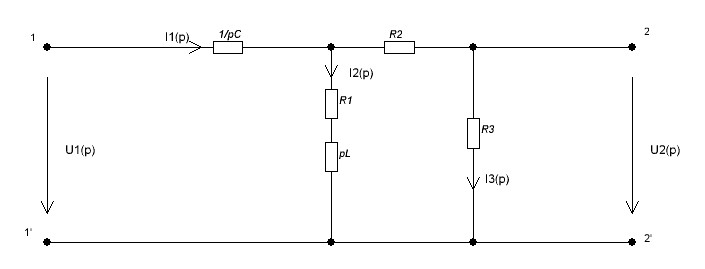
Рисунок 2.6 –Рассчитываемая цепь в операторном виде

На вход рассчитываемой цепи подается напряжение 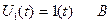, в операторном виде это напряжение будет равно .

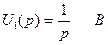Запишем операторное сопротивление цепи:

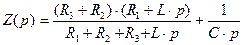(2.88)

Запишем выражение для первого тока 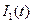в операторном виде:

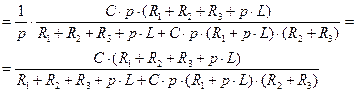(2.89)

Запишем выражение тока третьего через в операторной форме:

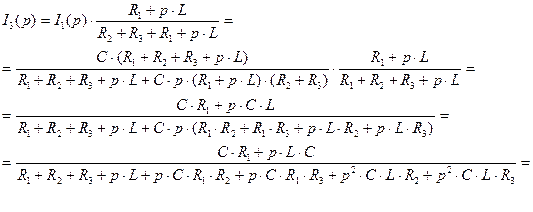
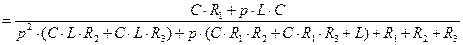(2.90)

Запишем выражение выходного напряжения 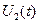в операторном виде:

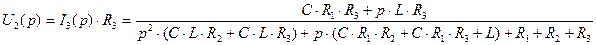
(2.91)

Обозначим числитель и знаменатель дроби (2.91) соответственно 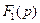и :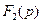

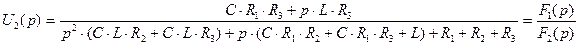
(2.92)

Приравниваем знаменатель выражения (2.92) к нулю - 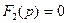и находим корни заданного квадратного уравнения:

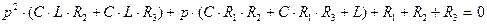(2.93)

Уравнение (2.93) абсолютно совпадает с уравнением (2.68) соответственно корни будут одинаковые:

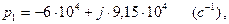(2.94)

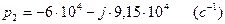(2.95)

Найдем производную от знаменателя дроби (2.92) то есть :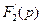

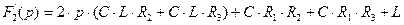(2.96)

Применяя теорему разложения, определим оригинал 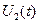по формуле:

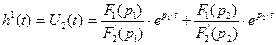(2.97)

Найдём, подставив вместо 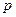в выражении (числитель) (2.92) первый корень характеристического уравнения (2.94):

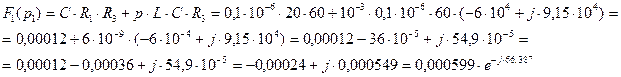
(2.98)

Найдём, подставив вместо 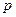в выражении (числитель) (2.92) второй корень характеристического уравнения (2.95):

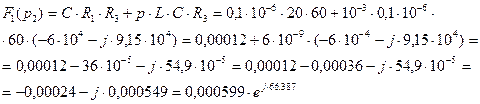
(2.99)

В выражение (2.96) подставим, первый корень характеристического уравнения (2.94) и получим:

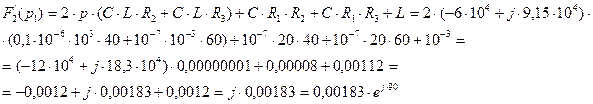
(2.100)

В выражение (2.96) подставим второй корень характеристического уравнения (2.95) и получим:

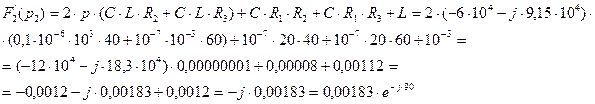
(2.101)

Подставляем найденные значения (2.98), (2.99), (2.100) и (2.101) в выражение (2.97):

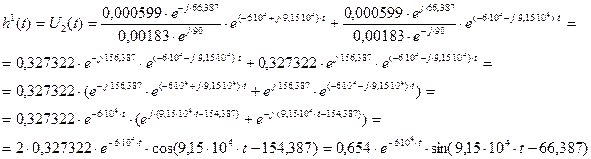
(2.102)

Расчет классическим методом (2.87) и операторным методом (2.102) совпадают, с учетом допустимой погрешности, можно сделать вывод, что переходная характеристика найдена, верно.

3 Расчет импульсной характеристики заданного четырехполюсника

Импульсной характеристикой 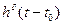линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие бесконечно короткого импульса бесконечно большой высоты и конечной площади этого импульса при нулевых начальных условиях:

Импульсная характеристика цепи численно равна реакции цепи на воздействие единичного импульса 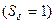, а размерность импульсной характеристики равна отношению размерности отклика цепи к произведению размерности внешнего воздействия на время.

Импульс бесконечно малой длительности, бесконечно большой высоты, площадь которого равна 1 называется единичным импульсом. Функция, определяющая единичный импульс, обозначается 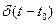и называется 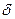- функцией или функцией Дирака:

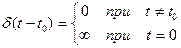
При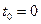

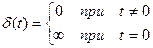
3.1 Расчет импульсной характеристики операторным методом в случае вещественных различных корней характеристического уравнения цепи

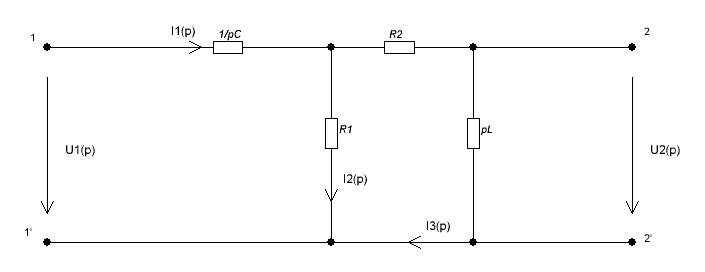
Рисунок 3.1 – Операторная схема заданного четырехполюсника

На вход рассчитываемой цепи подается напряжение 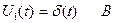, в операторном виде это напряжение, для расчета импульсной характеристики, будет равно .

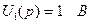Запишем операторное сопротивление цепи:

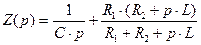(3.1)

Запишем выражение для первого тока 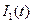в операторном виде:

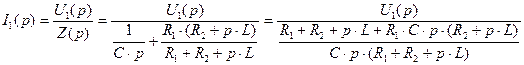
(3.2)

Запишем выражение тока третьего 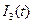через 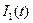в операторной форме:

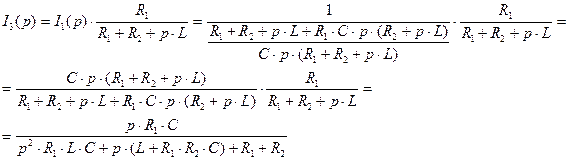
(3.3)

Запишем выражение для выходного напряжения 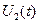в операторном виде:

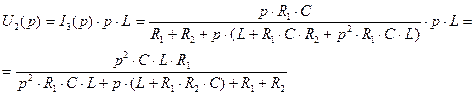(3.4)

Выполним обратное преобразование Лапласа с помощью теоремы разложения. Обозначим числитель и знаменатель дроби (3.4) соответственно 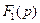и :

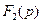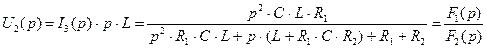(3.5)

Приравниваем знаменатель выражения (3.5) к нулю - 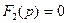и находим корни заданного квадратного уравнения:

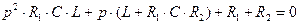(3.6)

Корни заданного уравнения будут совпадать с корнями при расчете переходной характеристики, так как заданные уравнения идентичны:

(3.7)

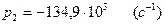(3.8)

Найдем производную от знаменателя дроби (3.5) то есть :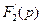

(3.9)

В соответствии с теоремой разложения 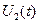имеет вид:

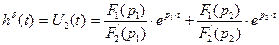(3.10)

Найдём подставив вместо 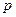в выражении (числитель) (3.5) первый корень характеристического уравнения (3.7):

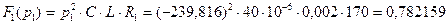(3.11)

В выражение (3.9) подставим, первый корень характеристического уравнения (3.7) и получим:

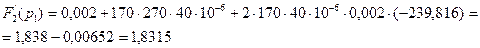(3.12)

Найдем, 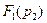подставив вместо 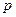в выражении (числитель) (3.5) второй корень характеристического уравнения (3.8):

(3.13)

В выражение (3.9) подставим, второй корень характеристического уравнения (3.8) и получим:

(3.14)

Подставляем найденные значения (3.11), (3.12), (3.13) и (3.14) в выражение (3.10):

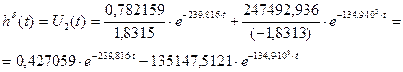(3.15)

Получили выражение, представляющее собой импульсную характеристику заданного четырехполюсника (3.15).

Графики переходной и импульсной характеристик, в случае когда корни характеристического уравнения являются вещественными различными, построены в системе Mathcad 2001 Professional и приведены в Приложении Б.

Данные расчёта переходной и импульсной характеристик в случае, если корни характеристического уравнения будут вещественными различными, приведены в таблице 3.1.

Таблица 3.1 – Данные расчета переходной и импульсной характеристик, в случае, если корни характеристического уравнения будут действительными

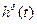
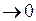
		0o
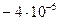
	1.82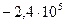
	0.81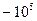
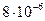
	0.398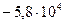
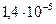
	0.199
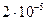
	0.101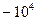
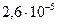
	0.01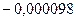
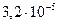
	0.009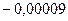
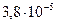
	0.0089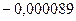
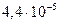
	0.0088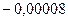
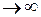
		0

3.2 Расчет импульсной характеристики четырехполюсника для случая комплексно – сопряженных корней характеристического уравнения. Рассмотрим на примере четырехполюсника, операторная схема замещения которого приведена на рисунке 3.2.

Рисунок 3.2 - Операторная схема заданного четырехполюсника

Параметры заданного четырехполюсника:

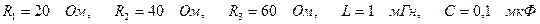
На вход рассчитываемой цепи подается напряжение 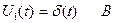, в операторном виде это напряжение, для расчета импульсной характеристики, будет равно .

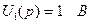Запишем операторное сопротивление цепи:

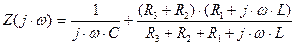(3.16)

Запишем выражение для первого тока в операторном виде:

(3.17)

Запишем выражение тока третьего 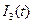через 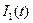в операторной форме:

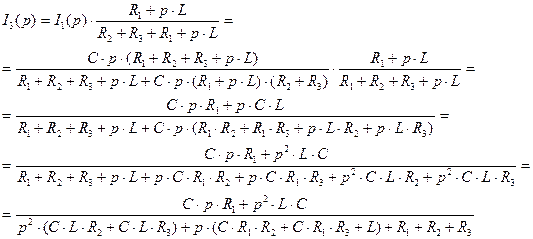(3.18)

Запишем выражение для выходного напряжения 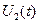в операторном виде:

(3.19)

Выполним обратное преобразование Лапласа с помощью теоремы разложения. Обозначим числитель и знаменатель дроби (3.19) соответственно 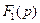и :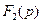

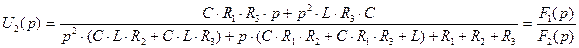
(3.20)

Приравниваем знаменатель выражения (3.20) к нулю - 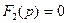и находим корни заданного квадратного уравнения:

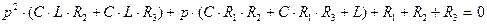(3.21)