
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие об аппроксимации функций. Виды аппроксимации. Интерполирование. Приближение и его оценка
Часто в результате экспериментальных данных или расчетов получаем зависимость 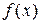 в виде определенного числа точек (в виде дискретного множества), то есть для функции неизвестна зависимость, а известны только некоторые её промежуточные результаты. Получению зависимостей для таких функций в требуемой области и служит задача об аппроксимации функций (рис. 5.1).
в виде определенного числа точек (в виде дискретного множества), то есть для функции неизвестна зависимость, а известны только некоторые её промежуточные результаты. Получению зависимостей для таких функций в требуемой области и служит задача об аппроксимации функций (рис. 5.1).
Аппроксимация функций – это нахождение функции 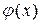 , максимальной близкой действительной функции
, максимальной близкой действительной функции 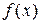 , так чтобы отклонение её, по крайней мере, в заданной области изменения аргумента x было наименьшим.
, так чтобы отклонение её, по крайней мере, в заданной области изменения аргумента x было наименьшим.
Функцию 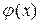 показывают аппроксимирующей.
показывают аппроксимирующей.
Подобный подход используется и в методе конечных элементов, где задаются аппроксимирующие функции для перемещений, которые в дальнейшем должны дать близкие к действительным перемещения (деформации) и усилия.
Для аппроксимации часто используют многочлены вида
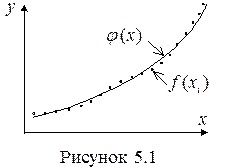
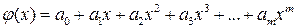 , (5.1)
, (5.1)
где коэффициенты ai подбирают из определенных условий так, чтобы достичь наименьшего отклонения многочлена от действительной функции.
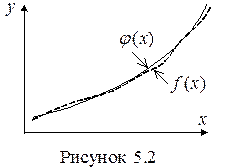 Если приближение строится на дискретном множестве точек, то аппроксимация называется точечной (рис. 5.1).
Если приближение строится на дискретном множестве точек, то аппроксимация называется точечной (рис. 5.1).
Если приближение строится для непрерывной функции на некотором отрезке  , то
, то
аппроксимация называется непрерывной или
интегральной (рис. 5.2).
Одним из основных видов точечной аппроксимации является интерполирование.
Оно состоит в следующем: задаем многочлен, которой должен принимать в известных точках хi те же значения yi, что и заданная дискретно функция y = φ (х); то есть в этих точках должно быть φ (хi) = yi, 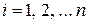 . При этом точки хi называются узлами интерполяции, а многочлен y (х) – интерполирующим многочленом. Интерполяция может быть глобальной (на всем участке изменения аргумента х) и локальной (кусочной) – на отдельных участках изменения функции.
. При этом точки хi называются узлами интерполяции, а многочлен y (х) – интерполирующим многочленом. Интерполяция может быть глобальной (на всем участке изменения аргумента х) и локальной (кусочной) – на отдельных участках изменения функции.
В случае большого количества точек, часто невозможно найти многочлен, который бы проходил через все эти точки (тем более, что и при получении точек в эксперименте могут быть погрешности и ошибки). В этих случаях находят такой многочлен, который проходил бы максимально близко от заданных точек. Понятие «близко» оценивается разными путями.
Одной из распространенных мер отклонения многочлена 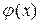 от заданной функции
от заданной функции 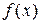 является среднеквадратичное приближение, определяемое
является среднеквадратичное приближение, определяемое
выражением 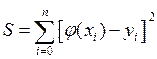 . (5.2)
. (5.2)
Задача состоит в подборе интерполирующего многочлена таким образом, чтобы S было наименьшим.
Приближение функции φ (х) к f (х) может оцениваться и на основе абсолютного отклонения Δ, равного
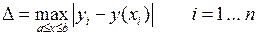 , (5.3)
, (5.3)
либо вводят понятие среднеквадратичного отклонения
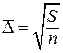 , (5.4)
, (5.4)
для которых задают допустимые величины отклонений (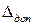 ).
).
Date: 2015-05-22; view: 6340; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |