
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Различные виды уравнений прямой в пространстве
1. Параметрические уравнения прямой в пространстве имеют вид
(18.1) 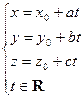 ,
,
где М0(х0,y0,z0) – точка, лежащая на прямой, а l(a,b,c) – ее направляющий вектор. Их вывод копирует соответствующие рассуждения из §13. Проведите его сами.
2. Канонические уравнения прямой в пространстве. Вспомним еще раз, что точка М(х,у,z) лежит на прямой l = [М0(х0,у0,z0), l(a,b,c)] тогда и только тогда, когда M0M || l, что равносильно пропорциональности координат этих векторов. Если все три координаты вектора l не равны 0, эту пропорциональность можно записать в виде
(18.2) 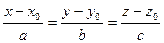 . (18.2)
. (18.2) 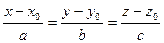 .
.
Это и есть каноническое уравнение прямой в пространстве. Оно аналогично опасной форме (13.5) канонического уравнения прямой на плоскости.
Заметим, что тройное равенство (18.2) есть краткая запись трех попарных равенств: 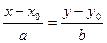 ,
, 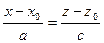 и
и 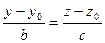 . Поскольку каждое из них является следствием двух других, тройное равенство (18.2) равносильно системе двух обычных, например
. Поскольку каждое из них является следствием двух других, тройное равенство (18.2) равносильно системе двух обычных, например
(18.3) 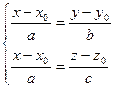 ,
,
которая называется системой канонических уравнений прямой в пространстве. Приведя первое из них к виду bx – ay + (ay0 + bx0) = 0, убедимся, что оно задает плоскость, параллельную Оz. Аналогично, второе уравнение системы (18.2) задает плоскость, параллельную Oy. Таким образом, система канонических уравнений задает прямую, как пересечение двух плоскостей, параллельных двум различным координатным осям.
Система (18.3), как и уравнение (18.2), имеет смысл только при a, b, c ¹ 0. Покажем, как будут выглядеть канонические уравнения прямой, если это условие не выполняется.
Случай 1: a, b ¹ 0, c = 0. В этом случае направляющий вектор l(a,b,0) прямой по признаку (17.8) параллелен плоскости z – z0 = 0, а сама прямая, имеющая с этой плоскостью общую точку М0(х0,y0,z0), лежит в ней. Поэтому мы можем, сохранив первое из уравнений (18.3), заменить второе уравнением z – z0 = 0. Получится система
(18.3') 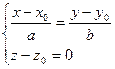 ,
,
задающая прямую как пересечение плоскостей, параллельных Oz и Оху.
Случай 2: a ¹ 0, b, c = 0. Тут направляющий вектор l(a,0,0) параллелен плоскостям z – z0 = 0 и у – у0 = 0, а сама прямая есть их пересечение и задается системой
(18.3'') 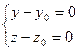 .
.
(18.3) Замечание. Форма записи (18.2) канонического уравнения прямой в пространстве весьма коварна. Кроме желания использовать ее, когда какой-то из знаменателей обращается в нуль, она провоцирует еще на одну ошибку: записать условие, что точка (x,y,z) не лежит на прямой, в виде
(18.4) 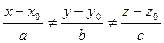
Так делать нельзя, ибо отрицание системы (18.3) – а, тем самым, и тройного равенства (18.2) – есть дизъюнкция 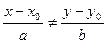 или
или 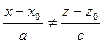 , а не конъюнкция (18.4).
, а не конъюнкция (18.4).
3. Уравнения прямой, заданной в пространстве двумя точками, получаются из уравнений (18.1) и (18.2) так же, как в случае прямой на плоскости. Выведите их сами.
§19. Взаимное расположение прямых и плоскостей в пространстве.
1. Взаимное расположение двух плоскостей. Возьмем две плоскости, заданные в АСК общими уравнениями:
П1: А1х + В1у + C1z + D1 = 0 (*)
П2: А2х + В2у + C2z + D2 = 0 (**)
и попытаемся, используя только данные уравнения, установить взаимное расположение этих плоскостей. Подобную задачу мы уже решали для прямых на плоскости; результаты для плоскостей в пространстве оказываются аналогичными.
(19.1) Теорема. Плоскости П1 и П2 параллельны в широком смысле тогда и только тогда, когда коэффициенты при х, у и z в их общих уравнениях пропорциональны, т.е.
(19.2) существует такое действительное число k, что А2 = kA1, В2 = kВ1, С2 = kС1.
При условии (19.2) плоскости П1 и П2 совпадают тогда и только тогда, когда
(19.3) D2 = kD1.
ð Параллельность плоскостей в широком смысле означает, что всякий вектор, параллельный одной из них, параллелен и другой. [20] Пусть выполнено условие (19.2). Тогда по признаку параллельности вектора и плоскости р(а,b,c) || П1 Û A1a + B1b + C1c = 0 Û k(A1a + B1b + C1c) = 0 Û A2a + B2b + C2c = 0 Û р(а,b,c) || П2. Значит, условие (19.2) влечет параллельность плоскостей. Обратно, пусть П1 || П2. Не умаляя общности, будем считать, что С1 ¹ 0. Векторы a(0,–C1, B1) и b(–C1,0,A1), параллельные П1, параллельны и П2. Отсюда по признаку параллельности вектора и плоскости имеем: a || П2 Þ –C1В2+B1С2 = 0 Þ 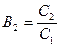 В1 и b || П2 Þ –C1A2+A1С2 = 0 Þ
В1 и b || П2 Þ –C1A2+A1С2 = 0 Þ  A1. Учитывая, что С2 =
A1. Учитывая, что С2 = 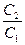 С1, получаем, что равенство (19.2) выполнено при k =
С1, получаем, что равенство (19.2) выполнено при k = 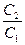 . Признак параллельности доказан.
. Признак параллельности доказан.
Признак совпадения плоскостей в одну сторону очевиден: если все коэффициенты уравнения (**) пропорциональны соответствующим коэффициентам уравнения (*), то эти уравнения равносильны. Обратно, если П1 = П2, то П1 || П2 и выполнено условие (19.2). Осталось взять произвольную точку М0(х0,у0,z0)ÎП1=П2, подставить ее координаты в уравнения (*) и (**) и заметить, что D2 = –(A2x0+B2y0+C2z0) = k(–A1x0–B1y0–C1z0) = kD1. ð
2. Прямая как пересечение двух плоскостей. Возьмем две непараллельные плоскости, заданные уравнениями (*) и (**) из п.1. Они пересекаются по прямой l, заданной системой
(19.4) 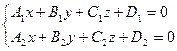 ,
,
которая называется системой общих уравнений прямой в пространстве. Очевидно, так можно задать любую прямую.
При решении задач на прямую, заданную общими уравнениями, бывает полезна
(19.5) Теорема. Вектор р(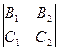 ,
, 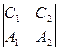 ,
, 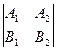 ) является направляющим для прямой, заданной системой (19.4).
) является направляющим для прямой, заданной системой (19.4).
ð Достаточно показать, что этот вектор параллелен обеим плоскостям, заданным уравнениями из системы (19.4). Применим признак параллельности вектора и плоскости: р || П1 Û А1 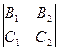 + В1
+ В1 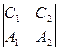 + С1
+ С1 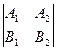 = 0 Û
= 0 Û 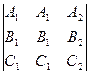 = 0. Но последнее равенство очевидно, ибо у определителя в его левой части – два одинаковых столбца. Аналогично проверяется и условие р || П2. ð
= 0. Но последнее равенство очевидно, ибо у определителя в его левой части – два одинаковых столбца. Аналогично проверяется и условие р || П2. ð
3. Взаимное расположение прямой и плоскости. Установим взаимное расположение прямой l = [М0(х0,y0,z0), р(a,b,c)] и плоскости П: Ax + By +Cz + D = 0. Признак их параллельности в широком смысле очевиден: l || П Û р || П Û
(19.6) Aa + Bb +Cc = 0
Теперь разберемся, когда прямая лежит в плоскости. Для этого необходимо и достаточно, чтобы прямая и плоскость были параллельны, и точка М0 лежала в плоскости. Задавая оба условия аналитически, получаем систему, составленную из равенства (19.6) и условия принадлежности точки М0 плоскости П:
(19.7) Ах0 + Ву0 + Сz0 + D = 0.
Наконец, прямая пересекает плоскость тогда и только тогда, когда не выполнено условие (19.6). Чтобы в этом случае найти точку пересечения, удобнее всего задать прямую l параметрическими уравнениями, подставить их в уравнение плоскости и найти соответствующее точке пересечения значение параметра.
4. Взаимное расположение двух прямых. (19.8) Лемма. Прямые
l = [М0(х0,y0,z0), р(a,b,c)] и m = [M1(х1,y1,z1), q(a1,b1,c1)] лежат в одной плоскости тогда и только тогда, когда векторы M0M1, p и q компланарны, т.е.
(19.9) 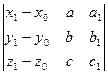 = 0.
= 0.
ð Пусть векторы M0M1, p и q компланарны. Это значит, что они параллельны некоторой плоскости a0. Проведем через точку М0 плоскость a || a0. Поскольку М0М1 || a, точка М1лежит в плоскости a. Кроме того, векторы p и q параллельны этой плоскости. Значит, прямые l и m лежат в ней. Обратно, пусть прямые l и m лежат в некоторой плоскости. Тогда векторы p и q параллельны ей, а точки M0 и M1 лежат в ней. Значит, вектор M0M1 тоже параллелен этой плоскости, что и завершает доказательство. ð
(19.10) Лемма. Прямые l и m совпадают тогда и только тогда, когда все три вектора M0M1, p и q коллинеарны.
ð То, что из совпадения прямых вытекает коллинеарность векторов, очевидно. Обратно, пусть векторы коллинеарны. Тогда прямая m и вектор M0M1 параллельны прямой l. Так как точка М0 лежит на этой прямой, на ней же лежит и точка М1. Значит, прямая m параллельна прямой l и имеет с ней общую точку, откуда l = m. ð
Теперь мы можем описать алгоритм выяснения взаимного расположения двух прямых. Сначала проверяем равенство (19.9). Если оно не выполнено, прямые скрещиваются. Если выполнено, проверяем коллинеарность векторов p и q. Если они не коллинеарны, прямые лежат в одной плоскости и не параллельны, т.е., они пересекаются. Если же p || q, проверяем, коллинеарны ли векторы M0M1 и p. Если да – прямые совпадают, если нет – параллельны в узком смысле.
Date: 2015-05-22; view: 634; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |