Короткі відомості про математичний апарат квантової механіки

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

УЖГОРОДСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ФІЗИЧНИЙ ФАКУЛЬТЕТ

В.Ю. Лазур, С.Ю. Медведєв, М.І. Карбованець, О.М. Карбованець

ПРАКТИКУМ З КВАНТОВОЇ МЕХАНІКИ

Навчально-методичний посібник

Ужгород – 2009

Автори. Практикум з квантової механіки (навчально-методичний посібник). – Ужгород: Видавництво УжНУ “Говерла”, 2009. – ХХХ с.

Рецензент:

доктор фізико-математичних наук, професор,

завідувач відділу теорії елементарних взаємодій ІЕФ НАН України

Гайсак М.І.

Відповідальний за випуск:

доктор фізико-математичних наук, професор,

декан фізичного факультету, завідувач кафедри теоретичної фізики

Лазур В.Ю.

Посібник створено на базі частини лекційного курсу "Квантова механіка", що читається студентам усіх спеціальностей фізичного факультету УжНУ. Він містить ряд основних ідей і методів квантової механіки в обсязі, достатньому для їх подальшого застосування в курсах теоретичної фізики та спецкурсах. Посібник містить завдання різного рівня складності, приведено детальні розв’язки запропонованих задач.

Посібник розраховано на студентів фізико-математичних та інженерно-технічних спеціальностей університетів.

Рекомендовано до друку методичною комісією фізичного факультету

(протокол № від 2009 року).

Зміст

Стор.

В С Т У П.. 4

1. Короткі відомості про математичний апарат квантовоїт механіки. 5

2. Вправи на закріплення розуміння формалізму КМ.. 10

2.1. Комутаційні співвідношення. 10

2.2. Імовірності результатів вимірювань, середні значення та дисперсії фізичних величин. 11

3. Найпростіші задачі квантової механіки. 14

3.1. Стаціонарні стани. 14

3.2. Проходження через потенціальні бар’єри. ………………………….27

3.3. Наближені методи розв’язання квантово-механічних задач……………..41

ЛІТЕРАТУРА.. Ошибка! Закладка не определена.

ВСТУП

Основна мета даного навчально-методичного посібника – допомогти читачеві оволодіти математичним формалізмом квантової механіки (КМ). Наразі цей формалізм успішно зарекомендував себе у розв’язанні задач як фундаментального, так і прикладного характеру. Відмітимо особливості КМ як наукової дисципліни. Створена на початку ХХ ст., КМ досягла блискучих успіхів у поясненні фізичних явищ та властивостей матерії, обумовлених закономірностями мікросвіту (спектри атомів, молекул, кристалів, явища надплинності та надпровідності, особливості теплоємності речовини, тощо). Більш того – на основі КМ створені нові матеріали з наперед заданими властивостями і нові прилади – прилади квантової електроніки. Тобто, КМ наразі фактично стала інженерною дисципліною. Проте, більш глибокий – світоглядний – рівень КМ все ще представляє собою хвилюючу таємницю. Серед провідних фізиків сучасності досі, після численних дискусій протягом ХХ ст., немає єдиної точки зору щодо тлумачення та інтерпретації певних гносеологічних аспектів та базових понять КМ. Особливо це стосується процесу квантового вимірювання, для описання якого вживаються такі поняття, як “редукція хвильового пакету”, “колапс хвильової функції”, тощо. Слід відмітити, що переважній частині фізиків відсутність розуміння вказаних методологічних аспектів до останнього часу не заважала: їм було достатньо розуміння КМ на “інструментальному рівні”, тобто вміння застосовувати формалізм КМ до розв’язання конкретних задач. Але в останнє десятиліття інтенсивно почали розвиватися нові, фантастично цікаві напрямки КМ: квантові комп’ютери, квантова телепортація, квантова криптографія тощо. З’ясувалося, що для успішного просування за цими напрямками недостатньо обмежуватися лише “інструментальним рівнем” розуміння КМ – необхідно виробити більш глибоке “інтерпретаційне” розуміння цієї надзвичайно цікавої дисципліни. Автори даного посібника, однак, вважають за потрібне попередити зацікавленого читача: над філософськими, “інтерпретаційними” поняттями КМ можна починати працювати лише після засвоєння її “інструментального рівня”. Інакше подібні спроби у кращому випадку перетворюються у “словесну еквілібристику”, а у гіршому – ведуть до профанації науки.

Отже, ми наполегливо рекомендуємо читачеві: на певний час відкласти інтригуючи і цікаві “інтерпретаційні” питання КМ і зайнятися, можливо менш цікавою, але необхідною працею – оволодінням математичним апаратом КМ та його застосуванням до розв’язання конкретних практичних задач. Даний посібник якраз для цього і призначений. У першому розділі посібника конспективно наводяться основні відомості з математичного формалізму КМ (для більш ґрунтовного вивчення вказаних питань читач може звернутися до праць [1-5]). Вправи для закріплення розуміння цього формалізму наведенні у розділі 2. Основна частина посібника, розділ 3, присвячена розв’язанню вибраних практичних задач КМ.

Короткі відомості про математичний апарат квантової механіки

Математичний апарат КМ докорінним чином відрізняється від математичного формалізму класичної механіки. Це обумовлено суттєвою відмінністю поведінки мікрооб’єктів (яка досліджується в КМ) порівняно з рухом класичних частинок. Відмітимо наступні три основні відмінності: 1) принципово імовірнісний характер поведінки мікрооб’єктів (на відміну від однозначного – лапласівського - детермінізму класичної механіки); 2) співвідношення невизначеностей фізичних величин (ФВ): є такі пари ФВ, для яких не існує фізичних станів, в яких вони одночасно мали б точні значення (нижче це твердження буде обговорюватися детальніше, а зараз нагадаємо відомий приклад: пара “координата та проекція імпульсу 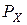” – їх дисперсі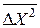ї і пов’язані співвідношенням невизначеності Гайзенберґа: 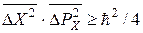); 3) дискретність можливих значень певних фізичних величин, наприклад, моменту імпульсу. Ці три особливості обумовили специфічність математичного формалізму КМ, необхідність використання нових понять, не притаманних класичній фізиці. Двома такими основними поняттями КМ є хвильова функція і оператор фізичної величини. Два вихідні твердження КМ. Твердження І: Стан фізичної системи задається хвильовою функцією. Твердження ІІ: У КМ фізичним величинам співставляються оператори. Нагадаємо основні положення, які розкривають зміст цих тверджень більш детально.

Хвильова функція (ХФ) 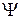в загальному випадку є комплексно-значною функцією деякого набору змінних 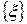і часу 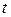: 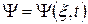. Наприклад, у випадку однієї безспінової частинки набір 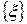є сукупністю її координат 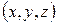(або деяких криволінійних координат ). Суть твердження І полягає в наступному: якщо задана хвильова функція 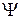системи, то ми можемо визначити амплітуду імовірності результату вимірювання будь-якої фізичної величини (див. нижче). Така інформація про фізичну систему з точки зору квантової механіки є максимально повною. Саме цей зміст вкладають у твердження, що 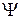визначає стан фізичної системи. Нагадаємо три основні вимоги до ХФ, які випливають з її ролі: вона має бути 1) однозначною, 2) неперервною і 3) обмеженою, точніше – квадратично інтегрованою (про можливі винятки йтиметься нижче). Сукупність ХФ, які описують всі можливі стани даної фізичної системи, утворюють лінійний простір (простір Гільберта). Це означає, що виконується принцип суперпозиції: якщо фізична система може знаходитися в станах , то вона може знаходитися і у стані 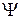, що є їх суперпозицією:

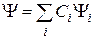, (1.1)

де коефіцієнти 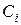- комплексні числа.

Серед усіх наборів особливий інтерес представляють так звані повні набори (базиси), за якими можна розкласти будь-яку ХФ. Надалі будемо використовувати лише ортонормовані базиси :

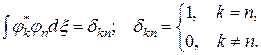(1.2)

Такими базисами є сукупності власних функцій операторів 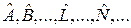фізичних величин 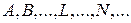Нагадаємо, що власною функцією оператора 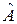називається функція, яка задовільняє рівнянню

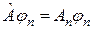. (1.3)

Числа у (1.3) називаються власними значеннями оператора 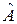, а їх сукупність – спектром оператора 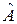. При вимірюванні величини 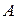одержують ті і тільки ті значення, які належать спектру 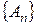. Це ілюструє один із інструментальних аспектів твердження ІІ.

Знання набору власних функцій дає можливість визначити імовірність того чи іншого результату вимірювання величини 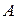у стані :

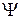, (1.4)

(вираз під знаком модуля – амплітуда вказаної імовірності). Формула (1.4) ілюструє один із інструментальних аспектів твердження І, а також розкриває фізичний зміст власних функцій. А саме, як випливає із (1.3) і (1.4), якщо система знаходиться в одному із власних станів 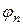, то при вимірюванні величини 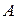ми із стовідсотковою імовірністю одержимо значення 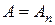, (а інші ).

Яким же чином у квантовій механіці конструюють оператори фізичних величин? Перш за все нагадаємо дві обмежувальні умови, що стосуються вказаних операторів. А саме, оператори фізичних величин повинні бути лінійними та ермітовими. Оператор 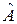називається лінійним, якщо образом суперпозиції є суперпозиція образів:

(1.5)

Лінійність операторів фізичних величин необхідна для забезпечення принципу суперпозиції. У свою чергу, ермітовість операторів потрібна для забезпечення дійсності власних значень оператора. Нагадаємо, що оператор називається ермітовим (або самоспряженим), якщо для довільних функцій 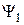та виконується співвідношення:

. (1.6)

Сформулюємо наступний принцип, який допоможе в конструюванні операторів фізичних величин: співвідношення між операторами фізичних величин у квантовій механіці має бути таким же, як співвідношення між цими величинами у класичній фізиці (існують деякі винятки з цього принципу, на яких ми тут не будемо зупинятися). Наприклад, момент імпульсу у класичній механіці визначається, як 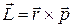, тому оператор моменту імпульсу у квантовій механіці має вигляд 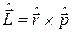. Оскільки переважна більшість фізичних величин є функціями координат та імпульсу, то нам залишилося відповісти на останнє питання: який явний вид операторів координати та імпульсу ? Відповідь – цей вид має бути таким, щоб дисперсії відповідних проекцій координати та імпульсу задовольняли співвідношенням невизначеності Гайзенберґа. А це буде тоді і тільки тоді, коли у групі операторів 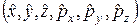виконуються наступні комутаційні співвідношення:

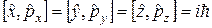, (1.7)

а всі інші комутатори дорівнюють нулю.

Нагадаємо, що комутатором 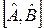операторів 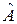і 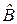називається вираз:

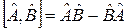. (1.8)

Можна довести наступне твердження (див. розділ 2, вправа): якщо оператори 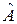і 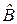не комутують, тобто , то

. (1.9)

Співвідношення (1.9) ілюструє другий інструментальний аспект твердження ІІ: оператори, як не комутативні у загальному випадку об’єкти, потрібні в КМ в силу відмінності 2). Нагадаємо, що дисперсією величини 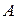називається вираз 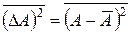, де 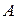- випадкове значення величини 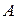, a - середнє значення. Можна довести, що середнє значення величини 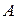у стані 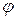визначається наступним співвідношенням (див. вправу 8): .

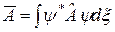Таким чином, залишилося підібрати такі оператори координат та імпульсів, які б задовольняли співвідношенням (1.7). У координатному представленні розв’язок (1.7) має вид (пропонуємо читачеві переконатися у цьому самостійно, звернувшись до вправи??? розділу 2):

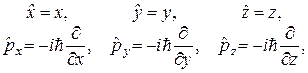(1.10)

або у векторній формі

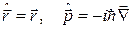. (1.11)

Тепер легко побудувати оператор кінетичної енергії

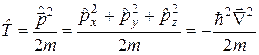(1.12)

та оператор моменту імпульсу:

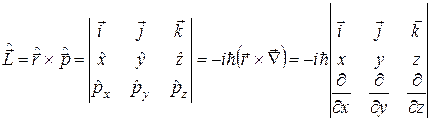. (1.13)

Звідси для операторів проекцій моменту імпульсу одержимо наступні вирази:

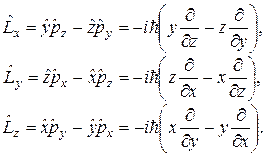(1.14)

Запроваджені вище оператори , , 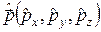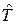та 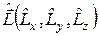будемо називати стандартними операторами. Комутативні співвідношення у цій сукупності операторів, а також розв’язки рівнянь на власні значення і власні функції цих операторів – відомі; вивчення вказаних питань пропонуємо зробити читачеві самостійно (диви вправи у наступному розділі).

Що ж стосується виду основного оператора КМ – оператора Гамільтона (або гамільтоніана) , який є оператором повної енергії 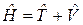, то він не має раз і назавжди заданого вигляду: незмінною залишається лише оператор кінетичної енергії 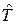, а вид оператора потенціальної енергії 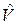залежить від конкретної задачі. Тому розв’язання певної квантово-механічної задачі розпочинається із моделювання гамільтоніана , фактично з моделювання 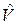. Часто такий вибір доводиться робити з урахуванням двох протидіючих обставин: з одного боку, аби модель була якомога точнішою, в 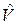потрібно включати найсуттєвіші взаємодії, а з іншого боку вираз 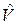має бути не занадто складним з огляду на можливість ефективного розв’язання відповідних рівнянь.

Наведемо приклади операторів Гамільтона деяких простих систем, з яких починається знайомство з квантовою механікою:

1) атом водню:

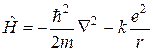; в системі СІ 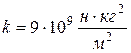; (1.15)

2) лінійний гармонічний осцилятор з власною частотою 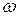і масою :

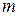; (1.16)

3) атом гелію:

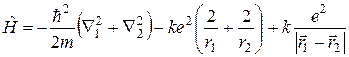. (1.17)

Рівняння на власні значення і власні функції оператора 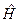у КМ називається стаціонарним рівнянням Шредінґера; воно має вид:

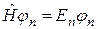. (1.18)

Переважна більшість теоретичних досліджень у КМ базується саме на рівнянні (1.18). У розділі 3 читачеві пропонується для розв’язання декілька практичних задач КМ, які фактично зводяться до розв’язання стаціонарного рівняння Шредінґера (1.18).

Зазначимо, що власні функції оператора Гамільтона 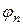є координатними частинами так званих стаціонарних станів

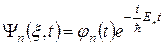, (1.19)

в яких система може знаходитися лише у випадках, коли гамільтоніан 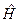явно не залежить від часу 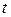, , 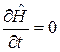тобто квантова система знаходиться у стаціонарних умовах. У загальному випадку еволюція системи описується (часовим) рівнянням Шредінґера:

. (1.20)

Неважко переконатися, що у випадку 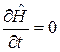хвильова функція (1.19) є розв’язком рівняння (1.20), якщо координатна функція 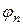задовольняє стаціонарне рівняння Шредінґера (1.18). Якщо ж 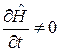, то стаціонарних розв’язків рівняння (1.20) не існує. У цьому випадку рівняння (1.20) описує еволюцію системи у часі. Таким чином, рівняння Шредінґера відображає більш загальну форму детермінізму – квантовий детермінізм: якщо відомий стан системи у початковий момент часу

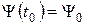, (1.21)

то, розв’язуючи рівняння (1.20) з початковою умовою (1.21), можна знайти стан 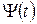системи у будь-який наступний момент часу .

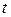Date: 2015-05-19; view: 693; Нарушение авторских прав