Состояния атомных электронов с разными моментами импульса

Зная закон квантования момента импульса, мы можем теперь полностью классифицировать состояние электрона в атоме. Действительно, электрон в атоме может обладать и ненулевым моментом количества движения 1, таким, что

|l|² = ћ²l(l + 1), l = 0, 1, 2, 3,..., (6.9)

а его проекция на заданную ось принимает при этом значения

l_z = ћm_l m_l = 0, ±1, ±2, ±3,..., ±1. (6.10)

Как уже упоминалось, вектор l принято называть орбитальным моментом

количества движения, l — орбитальным квантовым числом, a m_l —магнитным квантовым числом (оно определяет возможные значения проекции орбитального момента 1 на какую-либо ось). Отметим, что при обозначении m_l индекс «l» часто опускают, мы вводим его, чтобы не путать магнитное квантовое число с массой электрона.

Исторически (это пришло из оптики) состояния с различными l имеют

соответственно следующие наименования:

l = 0 называется «s-состоянием (от английского слова sharp),

l = 1 называется p-состоянием (от английского слова principal),

1 = 2 называется d-состоянием (от английского слова diffuse), и так далее

по алфавиту (f, g, h,...).

Раньше мы искали стационарное состояние атома водорода, предполагая, что решение является сферически-симметричным, т. е. зависит только от радиуса, но не от угловых переменных. Теперь снимем это ограничение.

Представим ψ-функцию в виде произведения угловой и радиальной компонент (что, оказывается, возможно):

ψ(r, θ, φ) = R(r) Y(θ, φ). (6.11)

В механике доказывается, что кинетическая энергия тела, движущегося в

поле центральных сил, может быть представлена как сумма кинетических

энергий радиального и вращательного движений, т. е.

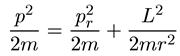
(6.12)

где момент импульса L является интегралом движения (сохраняющейся величиной) в центральном поле. Поэтому, если у тела есть ненулевой угловой момент, то эффективную потенциальную энергию радиального движения удобно представить в виде

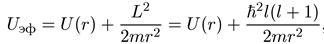(6.13)

где U(r) — обычная потенциальная энергия (в атоме — энергия кулоновского взаимодействия). Таким образом, формально уравнение Шредингера имеет такой же вид, как в радиально-симметричном поле, но с другим потенциалом (к кулоновскому потенциалу теперь добавляется центробежный).

Поскольку величина момента импульса тела, находящегося в поле центральных сил, сохраняется, то волновые функции частицы в таком поле являются собственными функциями оператора квадрата момента импульса:

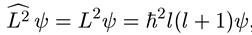, (6.14)

а уравнение Шредингера имеет следующий вид:

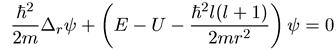
Радиальная волновая функция R(r) квантуется так же, как и ψ-функция

симметричного состояния (s-состояние). Обозначим соответствующие радиальные квантовые числа через n_r. Согласно вычислениям в чисто ском поле энергия электрона зависит только от квантового числа n, такого

что n = n_r + l, n_r = 1, 2, 3,..., l = 0, 1, 2, 3,...

Поэтому

n = 1, 2, 3,... (6.16)

Оно называется главным квантовым числом.

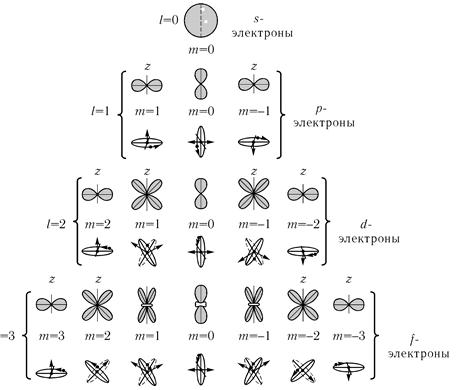
Рис. 6.4. Yгловые распределения плотности s-, р- и d-электронов в атоме при различных значениях магнитного квантового числа m_l.

Отметим, что радиальное квантовое число однозначно связано с числом узлов радиальной волновой функции (т. е. точек, в которых эта функция обращается в нуль) внутри области, в которой эта функция определена, а именно: число таких узлов равно n_r- 1. Как нетрудно убедиться, квантовое число n состояний частицы в бесконечно глубокой прямоугольной потенциальной яме (§. 4.5) точно так же связано с числом узлов соответствующей волновой функции внутри интервала ее определения.

На рис. 6.4 показаны угловые распределения плотности s-, р- и d-электронов в атоме при различных значениях магнитного квантового числа m_l.

Одновременно показано, какому движению электрона такие состояния соответствуют в боровской модели атома.

Распределение по углам обладает симметрией тела вращения около той оси, на которую фиксирована проекция момента импульса (на рисунке это ось z). При l = 0 электрон может находиться лишь в s-состоянии, которому соответствует полная шаровая симметрия. Следует заметить, что в модели атома Бора такого состояния просто нет. При l = 1 симметрия состояния соответствует симметрии типа диполя, при l = 2 возможна и симметрия типа квадруполя, когда максимум вероятности нахождения электрона соответ-

соответствует углу θ = π/4.

Распределение заряда по радиусу определяется радиальной волновой функцией R(r). Так, для сферически симметричных состояний заряд сферического слоя радиуса r и толщины dr равен

dQ(r) = ρ(r)dr = 4πr²R²(r)dr. (6.17)

У s-состояния волновая функция R (r) максимальна в нуле, а с ростом радиального квантового числа максимум ее смещается все дальше от центра.

Поскольку распределение заряда определяется согласно формуле (6.17),

произведением r²R²(r), то его максимум всегда смещен от центра атома,

но чем больше радиальное квантовое число, тем больше это смещение, т. е.,

грубо говоря, тем дальше расположен электрон от ядра.

На рис. 6.5 в качестве примера приведено распределение заряда в первых

состояниях водорода, по оси абсцисс отложено расстояние от центра атома,

выраженное в единицах боровского радиуса (радиуса первой водородной орбиты).

Числа на кривых показывают значение чисел n, l. Например, 31 означает n = 1,

1 = 1. Как видно, максимум состояния 10 (основное состояния атома водорода) как

раз соответствует радиусу первой боровской орбиты. Максимум зарядового распределения (расстояние электрона от ядра) смещается от центра атома с ростом n. Обратим еще раз внимание на

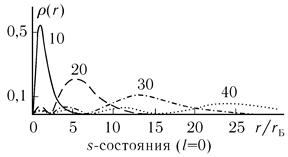
Рис. 6.5. распределение заряда в первых состояниях водорода

следующий факт: в теории Бора электроны движутся по плоским орбитам,

т. е. они не могут быть сферически симметричными. Согласно этой теории

нулевым моментом импульса обладал бы электрон, движущийся прямолинейно вдоль радиуса, но тогда по классическим законам он бы натолкнулся на ядро. В квантовой механике, в которой нет представления о движении электронов по орбитам, нет и никаких препятствий для реализации сферически симметричных состояний атома. Поэтому волновая электрона в атоме может быть сферически симметричной, т. е. зависеть

только от радиуса. В таком случае, как мы уже говорили, энергия определяется выражением

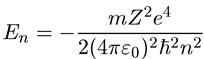
(6.18)

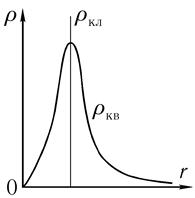
Рис. 6.6

На рис. 6.6 показано распределение электронной плотности по радиусу в боровской модели и при квантовомеханическом описании. Как указывалось выше, радиальная

волновая функция имеет число узлов, на 1 меньшее, чем номер соответствующего стационарного состояния. Это хорошо видно из рис. 6.5.

Итак, при заданной энергии (данном значении п) возможны состояния со всеми l, удовлетворяющими условию 0<l<n -1, а всего квантовое число l может принимать n различных значений. Однако при данном / электрон может находиться в 2l + 1 состояниях с различными значениями квантового числа m_l. Таким образом, нетрудно рассчитать чи-

число различных состояний, соответствующих одной и той же энергии, и оно

равно

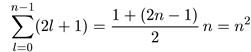
(6.19)

В этом случае говорят, что уровень вырожден, а число состояний, соответствующих одной и той же энергии, определяет кратность вырождения. В нашем случае получается 2n²-кратное вырождение. Несколько забегая вперед, отметим, что для стационарных состояний электрона в кулоновском поле имеет место еще дополнительное двукратное вырождение, связанное со спином электрона, так что на самом деле в кулоновском поле

электронный уровень оказывается 2n²-кратно вырожденным.

Pis 6.7

Обратимся теперь к вопросу о магнитном квантовом числе m_l. Если заряженная частица (в нашем случае — электрон) обладает ненулевым моментом количества движения, то это означает, что в системе имеются токи, следовательно, система должна обладать и магнитным моментом.

Рассмотрим классическую задачу о магнитном моменте электрона, движущегося по окружности (рис. 6.7). С движением заряженной частицы массой m со скоростью v по окружности радиусом r связаны как механический момент L, так и

магнитный μ.

Момент количества движения

L = m[ rv ], (6.20)

а магнитный момент

μ= IS, (6.21)

S-площадь кольца,

(6.22)

Коэффициент связи между μ и L называется гиромагнитным отношением.

Последнее не всегда равно е/(2m), и поэтому соотношение между μ и L

м

где I — протекающий ток, равный

I= -еv/(2πr),

a

S = πr²

охватываемого током. Но поскольку

[rv] = L/m,

то

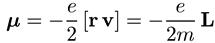
обычно записывается в виде

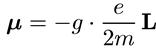, (6.23)

где коэффициент gназывается g-фактором и равен 1 для орбитального движения электрона. Ясно, что такая же связь справедлива для проекций:

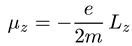
Как уже не раз говорилось, чтобы найти выражение для операторов физических величин, надо просто заменить численные равенства операторными, т. е. для оператора магнитного момента мы имеем

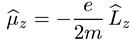, (6.25)

Отсюда сразу можно сказать, что правила квантования проекции магнитного момента электрона с заданным значением орбитального числа l такие же, как и для L_z:

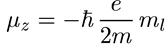. (6.26)

Итак, проекция момента количества движения электрона L_z и связанного с ним магнитного момента μ_z определяется одним и тем же квантовым числом m_l. Разница лишь в единицах: L_z выражается в единицах ћ, a μ_z — в единицах eћ/(2m) = 0,927-10^-23 Дж/Тл. Эта величина называется магнетоном Бора и обозначается μ_B. Таким образом, закон квантования проекции магнитного момента может быть записан в форме

μ_z = -μ_Bm_l. (6.27)

Теперь становится ясным происхождение названия mi как магнитного квантового числа.

Квантование орбитального момента количества движения, задаваемого

формулой

L = [rp], (6.28)

приводит к целым значениям l, а, значит, к нечетным значениям 2l + 1 числа возможных ориентации момента в пространстве. Если энергия зависит от ориентации момента, то в спектре как излучения, так и поглощения мы должны наблюдать расщепление основного перехода на 2l + 1 линий. Следовательно, появление в спектре нескольких близко расположенных по энергии линий (их называют мультиплетами) естественно связывать с таким расщеплением, т. е. рассматривать как результат существования зависимости энергии состояния от магнитного квантового числа mi. Однако одно из наиболее легко наблюдаемых подобных расщеплений — дуплеты в спектре щелочных металлов, и, в частности, дуплет натрия — не укладывается в эту простую схему. В самом деле, наличие двух ориентации означает, что должно выполняться условие 2l+ 1 = 2, откуда сразу следует, что l = 1/2;

но по правилу квантования момента l может быть лишь целым числом, и этот факт никак не соответствовует приведенным выше аргументам. Данное противоречие естественным образом снимается, если учесть существование собственного момента импульса, или спина, электрона.

Date: 2015-05-19; view: 1127; Нарушение авторских прав