Частица в одномерной прямоугольной

«потенциальной яме» с бесконечно высокими «стенками»

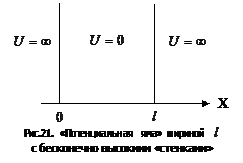
Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» шириной 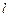с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси 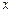) (рис.21):

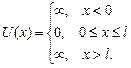
Поскольку функция зависит от одной координаты 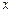, уравнение Шредингера имеет вид:

.

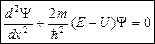Так как «стенки» ямы бесконечно высокие, то частица не проникает за пределы «ямы», поэтому вероятность обнаружения (а, следовательно, и волновая функция) за пределами «ямы» равна нулю. Из условия непрерывности функции на границах «ямы» волновая функция также должна обращаться в нуль.

Следовательно, граничные условия:

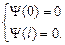
(27)     (28)

В пределах «ямы» 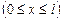уравнение Шредингера имеет вид:

.

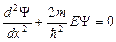Введем обозначение 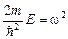, тогда получим уравнение, известное из теории колебаний (уравнение свободных незатухающих колебаний): .

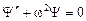Решение такого уравнения имеет вид:

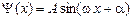. (29)

С учетом условия (27) из уравнения (29) следует: 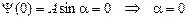. С учетом условия (28) из уравнения (29) следует: 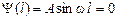, что возможно лишь в случаях 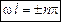( 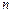=1, 2, 3…).

Следовательно, решение уравнения Шредингера имеет физический смысл не при всех значениях энергии 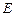, а лишь при значениях энергий удовлетворяющих соотношению:

.

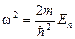Поскольку 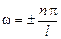, получаем 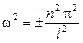, т.е.

.

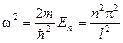Отсюда 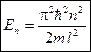( 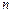=1,2,3…).

Таким образом, уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях 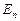, зависящих от целого числа 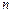. Следовательно, энергия 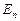частицы не может быть произвольной, а принимает лишь определенные дискретные значения, т.е. квантуется. Квантовые значения энергии 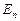называются уровнями энергии, а число 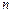, определяющее энергетические уровни частицы, называется квантовым числом.

Оценим энергетический интервал между двумя соседними уровнями:

,

,

.

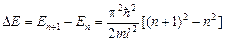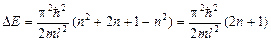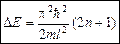Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию частицы никаких ограничений не накладывает.

Определим коэффициент в уравнении

.

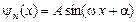С учетом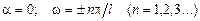

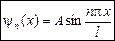. (30)

Для нахождения коэффициента воспользуемся условием нормировки:

.

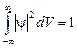Подставив в это выражение (30), получаем:

.

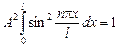Значение интеграла можно получить, умножив среднее значение 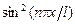(равное 1/2) на длину промежутка 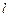. В результате получаем:

, .

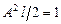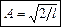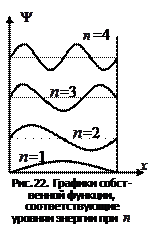Собственные функции имеют вид:

.

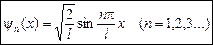Графики этой функции, соответствующие уровням энергии при 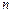=1,2,3,4, изображены на рис.22. Из рисунка видно, что частица в состоянии с 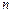=2 не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половинах ямы. Такое поведение частицы не совместимо с представлением о траекториях. Согласно классическим представлениям, все положения частицы в яме равновероятны.

Date: 2015-05-19; view: 512; Нарушение авторских прав