
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие о стационарном состоянии. Общее уравнение Шредингера. Уравнение Шредингера для стационарных состояний
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид
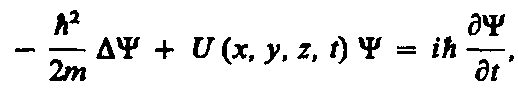 (1)
(1)
где ћ = h /(2p), т— масса частицы, D—оператор Лапласа 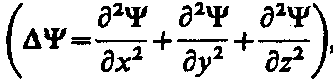 i — мнимая единица, U (х, у, z, t) — потенциальная функция частицы в силовом поле, в котором она движется, Y (х, у, z, t) — искомая волновая функция частицы.
i — мнимая единица, U (х, у, z, t) — потенциальная функция частицы в силовом поле, в котором она движется, Y (х, у, z, t) — искомая волновая функция частицы.
Уравнение (1) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (1) можно упростить, исключив зависимость Y от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функция U=U(x, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая — только времени, причем зависимость от времени выражается множителем 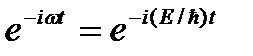 , так что
, так что
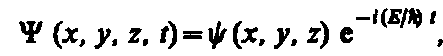 (2)
(2)
где Е — полная энергия частицы, постоянная в случае стационарного поля. Подставляя (2) в (1), получим
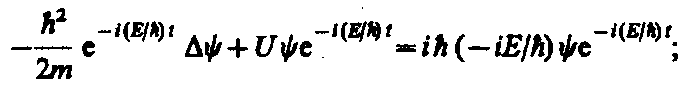
откуда после деления на общий множитель 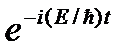 и соответствующих преобразований придем к уравнению, определяющему функцию y:
и соответствующих преобразований придем к уравнению, определяющему функцию y:
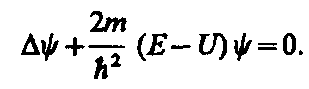 (3)
(3)
Уравнение (3) называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями y. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором — о дискретном спектре.
Принцип причинности в квинтовой механике
В классической механике, согласно принципу причинности — принципу классического детерминизма, по известному состоянию системы в некоторый момент времени (полностью определяется значениями координат и импульсов всех частиц системы) и силам, приложенным к ней, можно абсолютно точно задать ее состояние в любой последующий момент. Следовательно, классическая физика основывается на следующем понимании причинности: состояние механической системы в начальный момент времени с известным законом взаимодействия частиц есть причина, а ее состояние в последующий момент — следствие.
С другой стороны, микрообъекты не могут иметь одновременно и определенную координату, и определенную соответствующую проекцию импульса, поэтому и делается вывод о том, что в начальный момент времени состояние системы точно не определяется. Если же состояние системы не определено в начальный момент времени, то не могут быть предсказаны и последующие состояния, т. е. нарушается принцип причинности.
Однако никакого нарушения принципа причинности применительно к микрообъектам не наблюдается, поскольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в классической механике. В квантовой механике состояние микрообъекта полностью определяется волновой функцией Y(x, у, z, t), квадрат модуля которой |Y (x, у, z, t)|2 задает плотность вероятности нахождения частицы в точке с координатами х, у, z.
В свою очередь, волновая функция Y(х, у, z, t) удовлетворяет уравнению Шредингера, содержащему первую производную функции Y по времени. Это же означает, что задание функции Y0 (для момента времени t 0) определяет ее значение в последующие моменты. Следовательно, в квантовой механике начальное состояние Y0 есть причина, а состояние Y в последующий момент — следствие. Это и есть форма принципа причинности в квантовой механике, т. е. задание функции Y0 предопределяет ее значения для любых последующих моментов. Таким образом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего состояния, как того требует принцип причинности.
Движение свободной частицы
Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (x) = const и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера для стационарных состояний примет вид
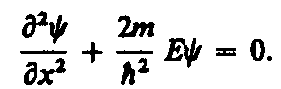 (1)
(1)
Прямой подстановкой можно убедиться в том, что частным решением уравнения (1) является функция y (х) = Аеikx, где А = const и k = const, с собственным значением энергии
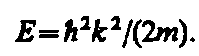 (2)
(2)
Функция 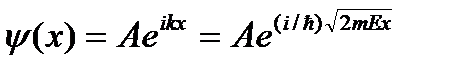 представляет собой только координатную часть волновой функции Y(x, t). Поэтому зависящая от времени волновая функция
представляет собой только координатную часть волновой функции Y(x, t). Поэтому зависящая от времени волновая функция
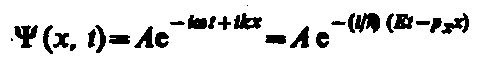 (3)
(3)
(здесь 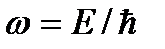 и
и 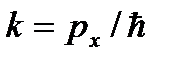 ). Функция (3) представляет собой плоскую монохроматическую волну де Бройля.
). Функция (3) представляет собой плоскую монохроматическую волну де Бройля.
Из выражения (2) следует, что зависимость энергии от импульса
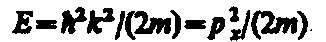
оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным.
Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства

т. е. все положения свободной частицы в пространстве являются равновероятными.
Частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Принцип соответствия. Квантование энергии и импульса частицы.
Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
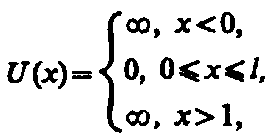
где l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 1).
| Рис. 1 |

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде
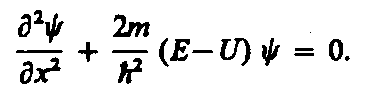 (1)
(1)
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х= 0 и х= 1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
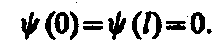 (2)
(2)
В пределах «ямы» (0 £ х £ l) уравнение Шредингера (1) сведется к уравнению
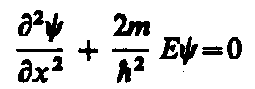
или
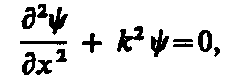 (3)
(3)
где
 (4)
(4)
Общее решение дифференциального уравнения (3):
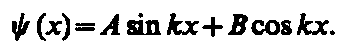
Так как по (220.2) y (0)=0, то В =0. Тогда
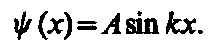 (5)
(5)
Условие (220.2) y (l) =A sin kl = 0 выполняется только при kl = np, где n — целые числа, т. е. необходимо, чтобы
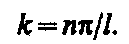 (6)
(6)
Из выражений (4) и (6) следует, что
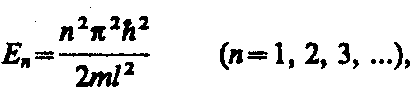 (7)
(7)
т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еn, зависящих от целого числа п. Следовательно, энергия Еn частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Еn называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Еn, или, как говорят, частица находится в квантовом состоянии n.
Подставив в (5) значение k из (6), найдем собственные функции:
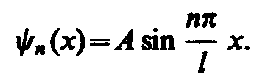
Постоянную интегрирования А найдем из условия нормировки, которое для данного случая запишется в виде
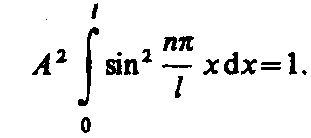
В результате интегрирования получим А = 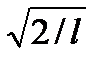 , а собственные функции будут иметь вид
, а собственные функции будут иметь вид
| Рис. 2 |
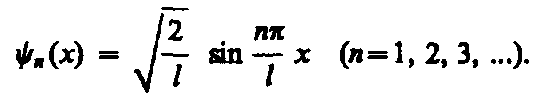 (8)
(8)
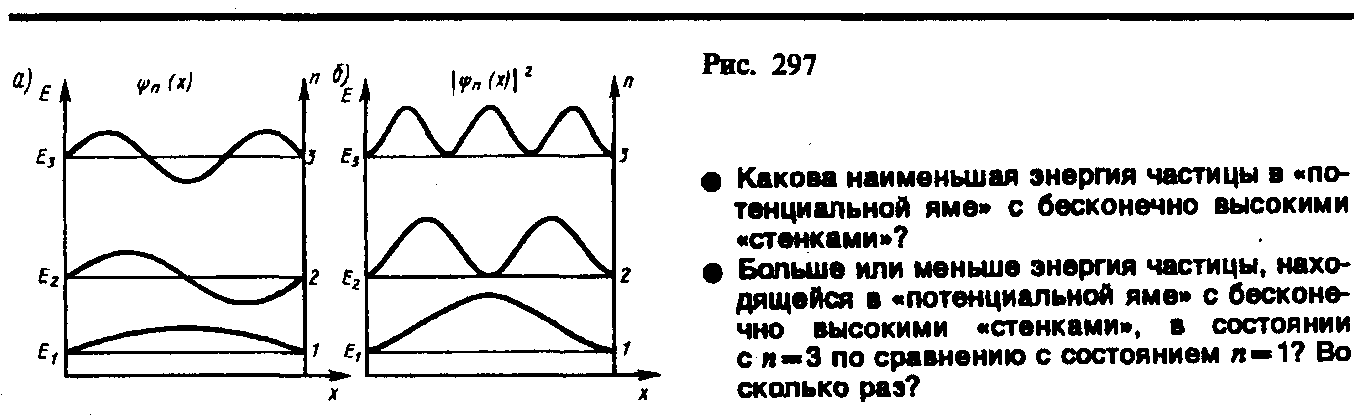 Графики собственных функций (8), соответствующие уровням энергии (7) при n = 1, 2, 3, приведены на рис. 2, а. На рис. 2, 6 изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная | yn (х)|2 = yn (х) y*n (х) для n= 1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n =2 частица не может находиться в середине «ямы», в то времякакодинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.
Графики собственных функций (8), соответствующие уровням энергии (7) при n = 1, 2, 3, приведены на рис. 2, а. На рис. 2, 6 изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная | yn (х)|2 = yn (х) y*n (х) для n= 1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n =2 частица не может находиться в середине «ямы», в то времякакодинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.
Из выражения (7) вытекает, что энергетический интервал между двумя соседними уровнями равен
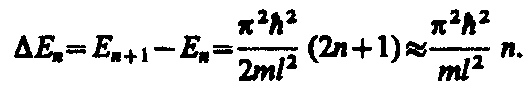 (9)
(9)
Из формул (9) и (7) следует, что при больших квантовых числах (n >>1) D En/En»2/ n <<1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.
Более общая трактовка принципа соответствия, имеющего огромную роль в современной физике, заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения, причем в определенных предельных случаях новая теория переходит в старую. Так, формулы кинематики и динамики специальной теории относительности переходят при v << с в формулы механики Ньютона. Например, хотя гипотеза де Бройля приписывает волновые свойства всем телам, но в тех случаях, когда мы имеем дело с макроскопическими телами, их волновыми свойствами можно пренебречь, т. е. применять классическую механику Ньютона.
Date: 2015-05-19; view: 1296; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |