
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоремы для эрмитовских операторов
Оператор 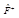 называется эрмитово сопряжённым по отношению к оператору
называется эрмитово сопряжённым по отношению к оператору 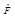 , если для любых функций
, если для любых функций 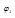 и
и 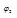 из пространства
из пространства 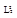 выполняется равенство:
выполняется равенство: 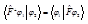 . Такая запись эквивалентна следующему соотношению:
. Такая запись эквивалентна следующему соотношению: 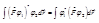 Оператор
Оператор 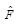 называется эрмитовым, если
называется эрмитовым, если 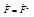 . Физическая величина
. Физическая величина 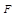 может принимать только те значения, которые принадлежат спектру её операторов. Если результатом действия оператора на функцию является число, умноженное на эту же функцию
может принимать только те значения, которые принадлежат спектру её операторов. Если результатом действия оператора на функцию является число, умноженное на эту же функцию 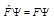 , то такая функция называется собственной функцией оператора
, то такая функция называется собственной функцией оператора 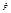 , а число
, а число  - собственным значением этого оператора. Вообще говоря, оператор может иметь несколько собственных функций и собственных значений, поэтому правильнее использовать запись
- собственным значением этого оператора. Вообще говоря, оператор может иметь несколько собственных функций и собственных значений, поэтому правильнее использовать запись  . Совокупность всех собственных значений оператора называют его спектром. Здесь
. Совокупность всех собственных значений оператора называют его спектром. Здесь 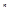 может пробегать как дискретный, так и непрерывный ряд значений. Выясним теперь, какие ограничения накладывает на собственные функции эрмитовость оператора.
может пробегать как дискретный, так и непрерывный ряд значений. Выясним теперь, какие ограничения накладывает на собственные функции эрмитовость оператора.
Теорема I. Все собственные значения эрмитового оператора действительны.  Умножим слева равенство
Умножим слева равенство  на функцию
на функцию  и проинтегрируем результат:
и проинтегрируем результат: 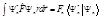 (2) Рассмотрим левую часть этого выражения. По определению эрмитова оператора мы можем записать для
(2) Рассмотрим левую часть этого выражения. По определению эрмитова оператора мы можем записать для
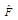 :
: 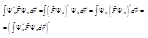 (3) последнее равенство следует из теории операторов (в данном курсе не рассматривается). Теперь, сравнивая выражение справа в (3) и выражение слева в (2), видим что
(3) последнее равенство следует из теории операторов (в данном курсе не рассматривается). Теперь, сравнивая выражение справа в (3) и выражение слева в (2), видим что 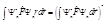 (4) Из выражения (4) следует, что, так как число слева равно своему сопряжённому, то это число действительное. Таким образом, теорема доказана.
(4) Из выражения (4) следует, что, так как число слева равно своему сопряжённому, то это число действительное. Таким образом, теорема доказана. 
Теорема II. Собственные функции линейного эрмитова оператора, принадлежащие различным собственным значениям, ортогональны друг другу, то есть 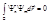 , если
, если 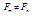 ,
, 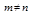 .
.  Запишем по определению собственного значения:
Запишем по определению собственного значения: 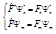 (5) Из условия самосопряжённости мы можем записать:
(5) Из условия самосопряжённости мы можем записать: 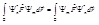 . Теперь, подставляя сюда формулы (5), получим:
. Теперь, подставляя сюда формулы (5), получим: 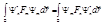 . Так как
. Так как 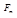 и
и 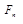 – константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим:
– константы, то мы можем вынести их за знак интеграла. Перенося интеграл в левую часть, получим: 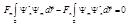 ,
, 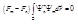 . По условию
. По условию  , поэтому,
, поэтому, 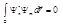 .
. 
Date: 2015-05-19; view: 642; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |