Теория возмущений. Возмущения, независящие от времени

З

2. Теоретическая часть 2.1.Частица в невозмущенном прямоугольном потенциале

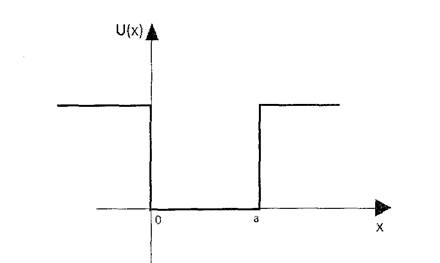
Рис 1. Прямоугольная потенциальная яма.

Рассмотрим микрочастицу, которая может совершать одномерное движение. Потенциальная энергия частицы в этой яме:

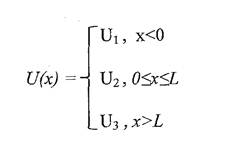
Пусть потенциальная энергия в области 2 равна нулю, а в областях 1 и 3 потенциальная энергия равна высоте ямы:

Чтобы описать движение квантовой частицы, решение уравнения Шрёдингера найдём сначала в отдельных областях 1, 2 и 3, затем потребуем непрерывности волновой функции и её производной на границах областей, в точках х = 0 и х = L

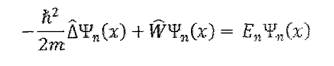
Решение в области 1:

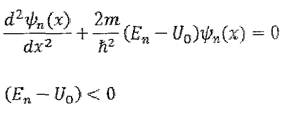
Обозначим:

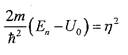
Теперь:

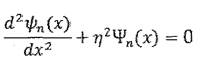
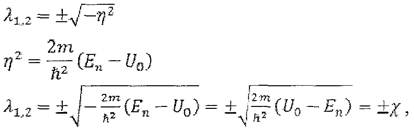
Получили однородное дифференциальное уравнение с

постоянными коэффициентами. Решение этого уравнения имеет вид:

, где 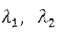корни характеристического

уравнения, которое в данном случае имеет вид: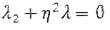

Корни характеристического уравнения:

- действительная величина

Решение дифференциального уравнения 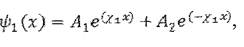здесь А1 и А2 - произвольные постоянные.

Решение в области 2:

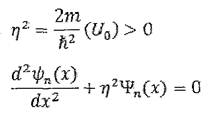
Решение этого уравнения имеет вид:

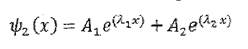, где 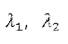корни характеристического

уравнения, которое в данном случае имеет вид: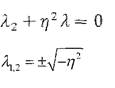

Корни характеристического уравнения мнимые:

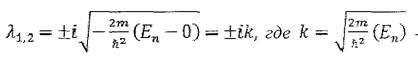- действительная

величина Решение дифференциального уравнения:

Это решение можно представит в действительной форме:

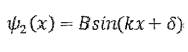
В области 3 решение находим аналогично решению в области 1:

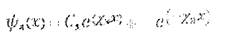
Получили решения-уравнения Шрёдингера областях 1, 2 и 3:

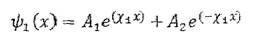
действительная величина

Решение дифференциального уравнения здесь А1 и А2 - произвольные постоянные.

Решение в области 2:

Решение этого уравнения имеет вид:

где

корни характеристического

уравнения, которое в данном случае имеет вид:

Корни характеристического уравнения мнимые:

действительная

величина Решение дифференциального уравнения:

Это решение можно представит в действительной форме:

В области 3 решение находим аналогично решению в области 1:

Получили решения-уравнения Шрёдингера областях 1, 2 и 3:

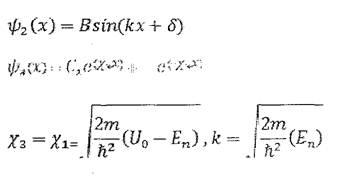
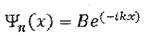
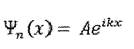
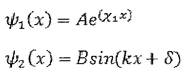
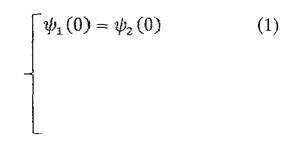
Ч1 N

Волновые функции можно рассматривать, как плоские волны.

Волну вида можно считать волной, распространяющейся вдоль положительного направления оси ОХ.

А волну вида можно считать волной, распространяющейся вдоль отрицательного направления оси ОХ.

Таким образом, решение уравнения Шрёдингера в области 1 можно рассматривать, как суперпозицию волны, падающей на барьер слева и волны, отраженной от барьера и распространяющейся вправо.

Аналогично, решение уравнения Шрёдингера в области 3 можно рассматривать, как суперпозицию волны, падающей на барьер справа и волны, прошедшей через барьер и распространяющейся вправо.

Если считать, что мы рассматриваем частицу, падающую на барьер слева, то в области 3 (за барьером) может существовать только прошедшая волна. Поэтому коэффициент ВЗ при волне, идущей из бесконечности к барьеру можно считать равным нулю.

Решения уравнения Шрёдингера в областях 1, 2 и 3:

Условия непрерывности волновой функции и её первой производной:

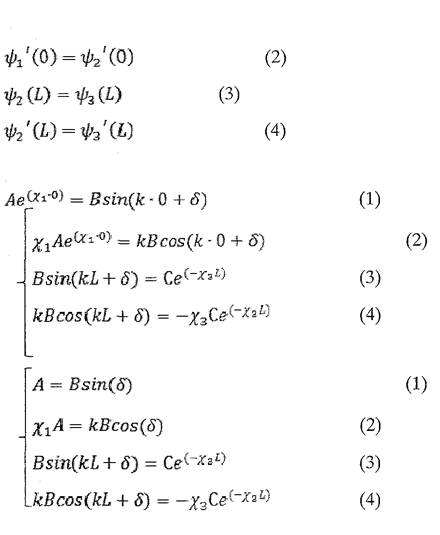
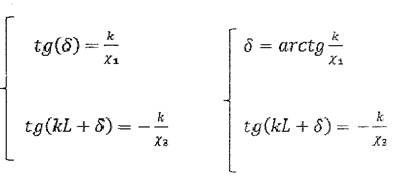
Разделим уравнение (1) на уравнение (2), а уравнение (3) на уравнение(4):

Получили трансцендентное уравнение:

Решением этого уравнения являются возможные уровни энергии, занимаемые электроном в невозмущенной яме. Для каждого значения энергии находим волновую функцию. Для этого определим коэффициенты А, В, С. Рассмотрим систему уравнений, возникающую из условий непрерывности волновой функции и её производной.

Разделим уравнение (1) на уравнение (2).

Из уравнения (3):

Из уравнения (1):

Для определения константы А воспользуемся условием нормировки волновой функции.

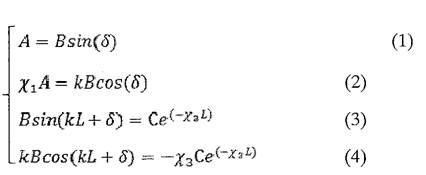
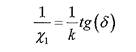
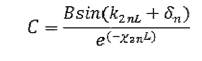
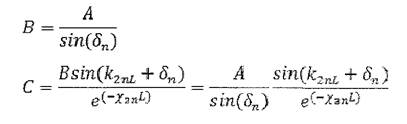
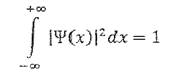
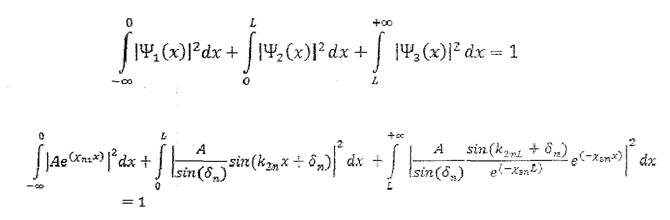
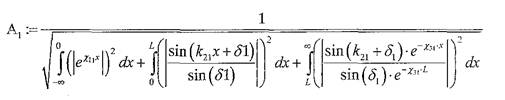
Отсюда:

Теория возмущений. Возмущения, независящие от времени

Точное аналитическое решение уравнения Шредингера можно найти -только для очень небольшого- числа задач. Во многих случаях удаётся решить задачу численно, но для этого нужны достаточно глубокие знания численных методов, в частности, методов решения дифференциальных уравнений. В то же время, довольно часто удаётся решить уравнение Шредингера приближенно, но с достаточной степенью точности, чтобы объяснить или даже рассчитать количественно какой-либо физический эффект. Одним из приближенных методов решения уравнения Шредингера является метод теории возмущений.

Этот метод удобно применять тогда, когда рассматриваемая физическая система незначительно отличается от другой системы, для которой известно аналитическое решение уравнения Шредингера, известны собственные значения энергии и соответствующие собственные функции. В таком случае первый шаг в решении поставленной физической задачи состоит в точном решении упрощенной задачи, а второй - в приближенном вычислении поправок, обусловленных малыми членами, отброшенными в упрощенной задаче. Предположим, что гамильтониан данной физической системы имеет вид

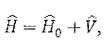
где 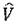представляет собой малую поправку (возмущение) к

«невозмущенному» оператору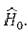

В данной работе мы рассматриваем возмущения 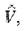не зависящие явно от времени (то же самое предполагается и в отношении 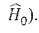Условия,

необходимые для того, чтобы можно было рассматривать оператор V как «малый», по сравнению с оператором 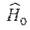будут определены ниже.

Задача теории возмущений для дискретного спектра может быть

сформулирована следующим образом.

Предполагается, что собственные функции 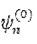и собственные

значения 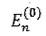дискретного спектра невозмущенного оператора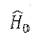

известны, то есть известны точные решения уравнения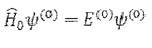

(2.1).

Требуется найти приближенные решения уравнения

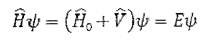
(2.2) то есть приближенные выражения для собственных функций 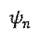и значений зозмущенного оператора 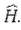Предполагается, что

собственные значения оператора 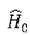не вырожденные, и считаем, что имеется дискретный спектр уровней энергии.

Вычисления удобно производить в матричном виде, для этого

разложим искомую функцию гр 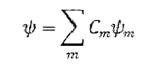по функциям :

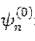(2.3) Подставляя это разложение в (2.2) получим:

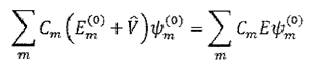
а домножив это равенство с обеих сторон на ц)_к и интегрируя, найдем

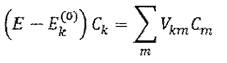
(2.4) Здесь выведена матрица 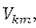оператора возмущения 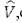эпределенная с

помощью невозмущенных функции :

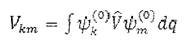(2.5)

Будем искать значения коэффициентов 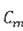и энергии Е в виде рядов:

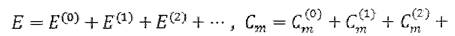•■-, где величины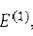

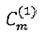- того же порядка малости, что н возмущение У. Величины Е&\- второго порядка малости и т.д.

Определим поправки к и-му собственному значению и собственной функции, в соответствии с чем полагаем, что 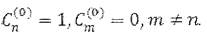Для

нахождения первого приближения подставим в уравнение (2.4)

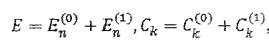, сохранив только члены первого порядка. Уравнение с к = п дает:

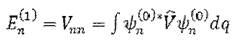(2.6)

Таким образом, поправка первого приближения к собственному значению Ь_ж равна среднему значению возмущения в состоянии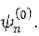

Уравнение (2.4) при кФп дает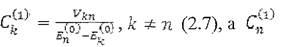

остается произвольным и должно быть выбрано так, чтобы функция

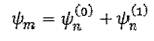была нормирована с точностью до членов первого порядка

включительно. Для этого надо полагать 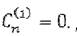Действительно, функция

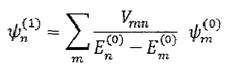(2.8),

ортогональна к а поэтому интеграл от 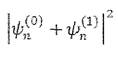отличается

на единицу лишь на величину второго порядка малости.

Формула (2.8) определяет поправку первого приближения к волновым функциям. Из нее видно условие применимости рассматриваемого метода:

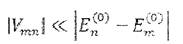(2-9),

то есть матричные элементы возмущения должны быть малы по сравнению с соответствующими разностями невозмущенных уровней энергии.

Определим еще поправку второго приближения к собственному

значению 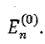Для этого подставляем в (2.4)

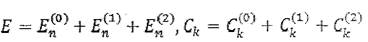и рассматриваем члены второго

порядка малости. Уравнение при к = п дает

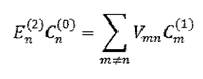
откула

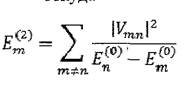
(2.10) Отметим, что поправка второго приближения к энергии нормального

состояния всегда отрицательна. Действительно, если 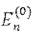соответствует

наименьшему значению, то все члены в сумме (2.10) отрицательны.

Дальнейшие приближения можно вычислить аналогичным образом. Полученные результаты непосредственно обобщаются на случай наличия у оператора также и непрерывного спектра (причем речь идет по-

прежнему о возмущенном состоянии дискретного спектра). Для этого надо только к суммам по дискретному спектру прибавить соответствующие интегралы по непрерывному спектру. Будем отличать различные состояния. непрерывного спектра индексом V, пробегающим непрерывный ряд

значений. Под у условно подразумевается совокупность значений величин,

достаточных для полного определения состояния (если состояние непрерывного спектра вырождены, что почти всегда и бывает, то задание

одной только энергии не достаточно для определения состояния; при этом волновые функции 1р.„ ' должны быть нормированы на дельта-функцию от величин у). Тогда, например, вместо (2.8) надо будет писать

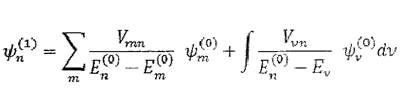
(2.11) И аналогично для других формул.

Алгоритм решения задачи:

1. Рассмотрим квантовую яму без возмущения, случай, когда собственные значения энергии электрона меньше, чем глубина потенциальной ямы обеих стенок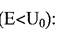

- исходя из граничных условий, решим трансцендентное уравнение и найдем набор собственных значений энергии электрона;

- запишем волновую функцию и пронормируем ее для нахождения одной из произвольных констант;

- построим графики зависимости волновой функции и вероятности обнаружения частицы в той или иной точки от собственных значений энергии.

2. Решим задачу с возмущением, для этого:

- найдем поправки к энергиям;

- найдем поправки к волновым функциям;

- построим графики зависимости волновой функции и вероятности-обнаружения частицы в той или иной точки от собственных значений энергии.

3. Сделаем выводы по полученным результатам.

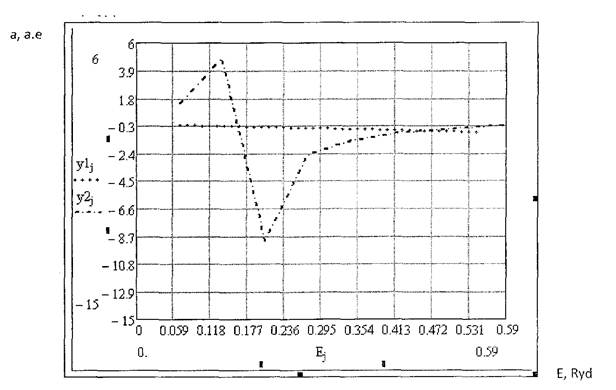
Получили два энергетических уровня.

Найдем коэффициенты А, 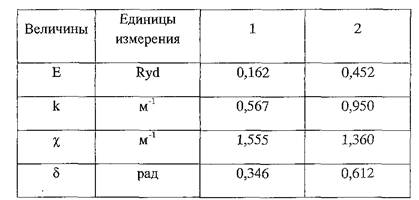В, 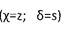С из условия нормировки волновой функции:

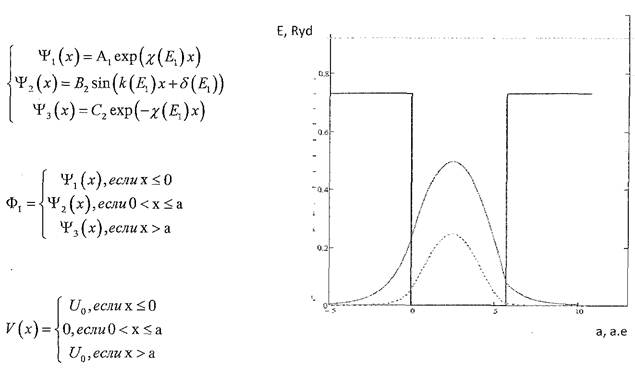
Построим графики зависимости волновой функции и вероятности обнаружения частицы в той или иной точке от собственных значений энергии:

Для первого энергетического уровня:

Для 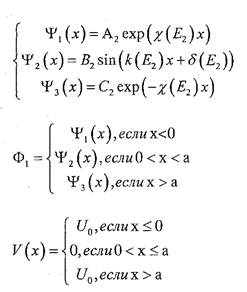второго энергетического уровня: