Уравнение Шредингера. В развитие идеи де-Бройля о волновых свойствах вещества австрийский физик Э

В развитие идеи де-Бройля о волновых свойствах вещества австрийский физик Э. Шредингер получил в 1926 г. уравнение, названное впоследствии его именем. В квантовой механике уравнение Шредингера играет такую же фундаментальную роль, как законы Ньютона в классической механике и уравнения Максвелла в классической теории электромагнетизма. Оно позволяет найти вид волновой функции частиц, движущихся в различных силовых полях. Вид волновой функции или Y-функции получается из решения уравнения, которое выглядит следующим образом

. (12.1)

Здесь m – масса частицы; i – мнимая единица; D – оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых производных по координатам

.

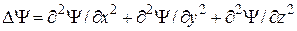Буквой U в уравнении (12.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу.

Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других уравнений. Если силовое поле, в котором движется частица, стационарно (т.е. постоянно во времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера состоит из двух множителей, один из которых зависит только от координат, другой – только от времени

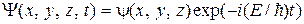. (12.2)

Здесь Е – полная энергия частицы, которая в случае стационарного поля остается постоянной; 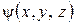– координатная часть волновой функции. Чтобы убедиться в справедливости (12.2), подставим его в (12.1):

.

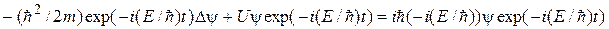В результате получим

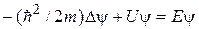. (12.3)

Уравнение (12.3) называется уравнением Шредингера для стационарных состояний. В дальнейшем мы будем иметь дело только с этим уравнением и для краткости будем называть его просто уравнением Шредингера. Уравнение (12.3) часто записывают в виде

.

В квантовой механике большую роль играет понятие оператора. Под оператором подразумевается правило, посредством которого одной функции, обозначим ее 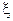сопоставляется другая функция, обозначим ее f. Символически это записывается следующим образом

,

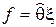здесь 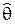– символическое обозначение оператора (можно было взять любую другую букву со «шляпкой» над ней, например 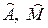и т. д.). В формуле (12.1) роль 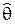играет D, роль 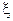– функция 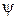, а роль f – правая часть формулы. Например, символ D означает двукратное дифференцирование по трем координатам, х, у, z, с последующим суммированием полученных выражений. Оператор может, в частности, представлять собой умножение исходной функции 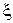на некоторую функцию U. Тогда 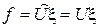, следовательно, 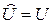. Если рассматривать функцию U в уравнении (12.3) как оператор, действие которого на Y-функцию сводится к умножению 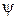на U, то уравнение (12.3) можно записать так:

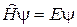. (12.4)

В этом уравнении символом 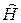обозначен оператор, равный сумме операторов 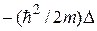и U:

.

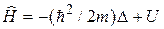Оператор 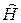называют гамильтонианом (или оператором Гамильтона). Гамильтониан является оператором энергии Е. В квантовой механике другим физическим величинам также сопоставляются операторы. Соответственно, рассматриваются операторы координат, импульса, момента импульса и т. д. Для каждой физической величины 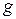составляется уравнение, аналогичное (12.4). Оно имеет вид

,

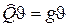где 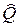– оператор, сопоставляемый g. Так, например, оператор импульса определяется соотношениями

; ; ,

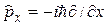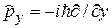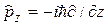или в векторном виде , где Ñ – градиент.

В разд. 10 мы уже обсуждали физический смысл Y-функции: квадрат модуля Y -функции (волновой функции) определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:

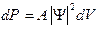, (12.5)

Поскольку квадрат модуля волновой функции равен произведению волновой функции на комплексно сопряженную величину 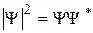, то

.

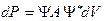Тогда вероятность обнаружения частицы в объеме V

.

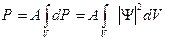Для одномерного случая

.

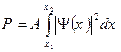Интеграл от выражения (12.5), взятый по всему пространству от 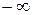до 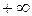, равняется единице:

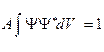
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т. е. вероятность достоверного события, которая равна 1.

В квантовой механике принимается, что волновая функция допускает умножение на отличное от нуля произвольное комплексное число С, причем 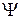и С Y описывают одно и то же состояние частицы. Это позволяет выбрать волновую функцию так, чтобы она удовлетворяла условию

(12.6)

Условие (12.6) называется условием нормировки. Функции, удовлетворяющие этому условию, называются нормированными. В дальнейшем мы всегда будем полагать, что рассматриваемые нами Y-функции являются нормированными. В случае стационарного силового поля справедливо соотношение

,

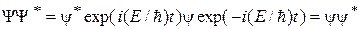т. е. плотность вероятности волновой функции равна плотности вероятности координатной части волновой функции и от времени не зависит.

Свойства Y -функции: она должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек) и иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.

В уравнение Шредингера в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида 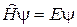имеют решения, удовлетворяющие стандартным условиям, не при любых, а лишь при некоторых определенных значениях параметра (т. е. энергии Е). Эти значения называются собственными значениями. Решения, соответствующие собственным значениям, называются собственными функциями. Нахождение собственных значений и собственных функций, как правило, представляет собой весьма трудную математическую задачу. Рассмотрим некоторые наиболее простые частные случаи.

Date: 2015-05-18; view: 541; Нарушение авторских прав