Следствия из преобразований теории относи­тельности

Рассмотрим наиболее важные следствия преобра­зований Лоренца.

а) Длина тел в разных системах.

Преобразова­ния Лоренца показывают, что одно и то же тело имеет раз­ные линейные размеры в системе, в которой оно покоится, и в системе, находящейся в движении по отношению к этому телу. Предположим, что некоторый стержень, покоящийся в системе ХУZ, расположен в направлении оси ОХ и имеет в этой системе длину l (равную разности координат его конца и начала):

l=x ₂ – x ₁ .

Какова длина этого стержня в штрихованной коорди­натной системе, движущейся относительно стержня со скоро­стью υ в направлении его длины?

Для того чтобы найти эту длину l, нужно ее выразить как разность координат конца и начала стержня в штрихо­ванной системе х ₂ ’ и x ₁ ’, при этом, пользуясь преобразова­ниями Лоренца, надо координаты х ₂ ’ и x ₁ ’ взять в один и тот же момент времени, определенный в штрихованной, системе. Таким образом, связывая х ₂ ’ и x ₁ ’ с x ₂ и x ₁ надо брать фор­мулу (8), содержащую время штрихованной системы; полагая это время постоянным, имеем:

;

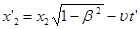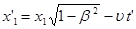
откуда следует:

x ₂ ’ – x ₁ ’= (x ₂ – x ₁) 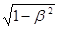или l’=l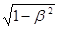

Стержень в координатной системе, движущейся отно­сительно него, короче, чем в системе, где стержень по­коится: Если бы мы взяли стержень, покоящийся в штрихован­ной системе, длина его была бы l’= x ₂ ’ – x₁’; в нештрихо­ванной системе его длина будет l= x ₂ – x ₁; теперь надо измерения вести в один к тот же момент времени нештрихо­ванной системы l. Пользуясь преобразованиями Лоренца (7), выражаем x ₂ и x ₁через x ₂ ’ и x₁’. Имеем:

x₂ – x₁= (x₂ ‘– x₁ ‘) 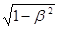или l=l’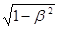

т. е. снова стержень длиннее в системе, в которой он по­коится. Заметим, что размеры тел в направлении осей ОУ и ОZ одинаковы в обеих системах.

Этот вывод теории относительности заменяет гипотезу о сокращении размеров тел, движущихся относительно эфира. По теории относительности стержень имеет наибольшую длину в той системе, относительно которой он покоится.

б) Длительность события в разных системах.

Длительность события также различна в разных координатных системах. Предположим, что в точке А с координатой х в нештрихованной координатной системе ХУZ, происходит некоторое событие, длительность которого равна τ = t₂ – t₁, где t₂ и t₁ моменты времени конца и начала этого события, отсчитанные в координатной системе ХУZ. Какова будет длительность τ ‘= t₂ ‘– t₁’ этого события в штрихованной координат­ной системе Х'У’Z’. Мо­ментам t₁ и t₂, отмеченным в координатной системе ХУZ, соответствуют моменты, t₂’ и t₁’ отмеченные в координатной системе Х'У'Z' для точки А, т. е. для од­ного и того же значения координаты х. Нам, следо­вательно, надо применить формулу преобразования (8), свя­зывающую t’ и t при одном и том же значении х. Таким образом, имеем:

t₁’ 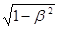= t₁ – xυ/c²; t₂’ 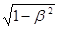= t₂ – xυ/c²

откуда следует

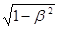(t’₂ – t’₁) = t₂ – t₁ или τ’ = τ /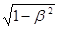

Промежуток τ ' будет больше τ.

Можно поставить и обратную задачу. Пусть в штрихо­ванной системе (х’ постоянно) длительность некоего события τ ' = t’₂ – t’₁ . Какова будет длительность этого события в не­штрихованной системе?

Для ответа используем преобразование (8), в котором х' положим постоянным. Тогда получим:

τ = τ’ /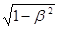

Теперь промежуток τ будет больше τ’. Отсюда полу­чаем следующее заключение: длительность события, про­исходящего в некоторой точке А, меньше по отношению к той координатной системе^ относительно которой точка А покоится.

Date: 2015-05-18; view: 710; Нарушение авторских прав