
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантовые системы и их свойства
Квантовые системы и их свойства.
Распределение вероятностей по энергиям в пространстве.
Статистика бозонов. Распределение Ферми-Эйнштейна.
Статистика фермионов. Распределение Ферми-Дирака.
Квантовые системы и их свойства
В классической статистике предполагается, что частицы составляющие систему подчиняются законам классической механики. Но для многих явлений при описании микрообъектов необходимо использовать квантовую механику. Если система состоит из частиц, подчиняющихся квантовой механике, то будем её называть квантовой системой.
К принципиальным отличиям классической системы от квантовой относятся:
1) Корпускулярно-волновой дуализм микрочастиц.
2) Дискретность физических величин, описывающих микрообъекты.
3) Спиновые свойства микрочастиц.
Из первого следует невозможность точного определения всех параметров системы, определяющих её состояние с классической точки зрения. Этот факт нашел отражение в соотношении неопределенностей Гейзендберга: 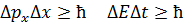
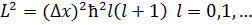
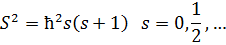
Для того чтобы математически описать эти особенности микрообъектов в квантовой физике, величине ставится в соответствие линейный эрмитов оператор, который действует на волновую функцию 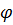 .
.
Собственные значения оператора определяют возможные численные значения этой физической величины, среднее по которым совпадает со значением самой величины.
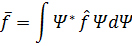
Так как импульсы и коэффициенты микрочастиц системы не могут быть измерены одновременно, волновую функцию представляют либо как функцию координат:

Либо, как функцию импульсов:
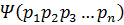
Квадрат модуля волновой функции определяет вероятность обнаружения микрочастицы в единице объёма:
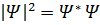
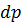 (
(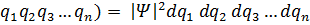
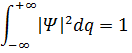
Волновая функция, описывающая конкретную систему, находится как собственная функция оператора Гамельтона:
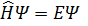 -Стационарное уравнение Шредингера.
-Стационарное уравнение Шредингера.
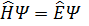 - Нестационарное уравнение Шредингера.
- Нестационарное уравнение Шредингера.
В микромире действует принцип неразличимости микрочастиц.
Если волновая функция 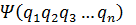 удовлетворяет уравнению Шредингера, то функция
удовлетворяет уравнению Шредингера, то функция 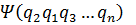 так же удовлетворяет этому уравнению. Состояние системы не изменится при перестановки 2 частиц.
так же удовлетворяет этому уравнению. Состояние системы не изменится при перестановки 2 частиц.
Пусть первая частица находится в состоянии а, а вторая в состоянии в.
Состояние системы описывается: 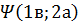
Если частицы поменять местами, то: 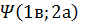 так как перемещение частицы не должно сказаться на поведении системы.
так как перемещение частицы не должно сказаться на поведении системы.
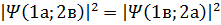
Это уравнение имеет 2 решения:
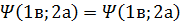
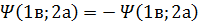
Оказалось, что первая функция реализуется для частиц с целым спином, а вторая с полуцелым.
В первом случае 2 частицы могут находиться в одном состоянии:

Во втором случае: 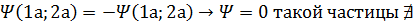
Частицы первого типа называются бозонами спин целый), частицы второго типа- фемионами (для них справедлив принцип Паули.)
Фермионы: электроны, протоны, нейтроны…
Бозоны: фотоны, дейтроны…
Фермионы и бозоны подчиняются неклассической статистике. Чтобы увидеть отличия, подсчитаем число возможных состояний системы, состоящий из двух частиц с одной энергией по двум ячейкам в фазовом пространстве.
1) Классические частицы различны. Возможно проследить за каждой частицей в отдельности.
Классические частицы:
| аа | - |
| - | аа |
| а | а |
Бозоны:
| ав | - |
| - | ав |
| а | в |
| в | а |
Фермионы:
| а | а |
Date: 2015-05-17; view: 674; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |