Умножение комплексных чисел

Z=a+ib, W=c+id ZW = (a+ib)(c+id)= ab+iad+ibc+i*ibd= ab-bd+i(ad+bc)/

Здесь принято основное свойство комплексных чисел: возможное наличие в комплексном числе слагаемого при котором стоит «интересный» множитель – i. Оно интересно тем, что квадрат этого числа равен минус единице. Этим оно и необычно, т.к. квадрат любого действительного числа (за исключением числа ноль) больше нуля.

В самой последовательности изложения, можно сделать вывод о значимости факторов определяющих комплексное число. Хотя число i есть то, что отличает его от действительного числа, сам порядок изложения подчёркивает большую важность именно общности между двумя типами чисел.

Но комплексные числа замечательны тем, что допускают простое представление в виде вектора. Это можно увидеть уже из закона сложения двух векторов.

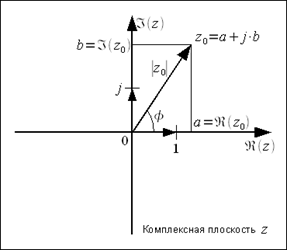
Рисунок 2. Он поможет понять, что комплексное число можно представить в виде 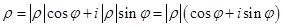. Здесь 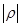(именно в «прямых» скобках, называющихся модулем) мы можем понимать просто как длину вектора, или как говорят математики модулем комплексного числа. Читателю не надо бояться наличия косинуса и синуса. Их смысл заключается в том, что 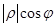это проекция на ось X (горизонтальная ось), а 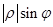- проекция комплексного числа на ось Y (вертикальная ось). От синусов и косинусов можно перейти к так мнимой экспоненте, т.е. 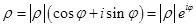. Пользу от этого представления мы поймём, когда будем конкретизировать умножение комплексных чисел. А именно пусть нам надо умножить два числа 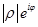и 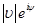. Тогда 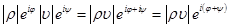. Т.е. если нам надо умножить два комплексных числа, то надо умножить их модули и сложить фазы.

Для дальнейшего нам не потребуется визуализации операций сложения и умножения комплексных решений. Но для «очистки совести» здесь приведены рисунки демонстрирующие сложение и умножение чисел.

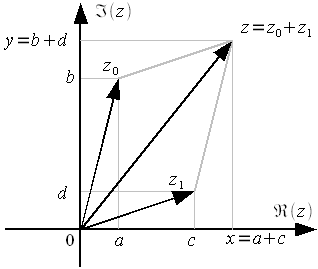
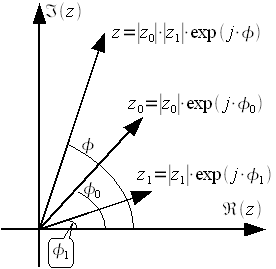
Рис 3. Сложение комплексных чисел Рис 4. Умножение комплексных чисел

Важный случай умножения комплексных чисел это умножение двух комплексно сопряжённых чисел. Из комплексного числа сопряжённое, ему получается очень просто надо изменить знак перед его второй частью: Z = a+ib, а сопряжённое к нему число Z* = a-ib. Если число умножить на его комплексное сопряжение, то результатом будет число Z² = a²+b². Это число равно квадрату «длины» комплексного числа и оно всегда положительно и вещественно. Последние обстоятельства имеют важное значение для построения математической теории. Результат, полученный здесь можно легко вывести, если при умножении использовать экспоненциальную запись числа. Чтобы в этой записи получить комплексное сопряжение надо просто изменить знак фазы.

.

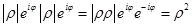Если читателю покажутся промежуточные выкладки утомительными, то важен их результат. В сухом остатке надо помнить закон сложения комплексных числе, а он устроен так-же как и для обычных чисел. Плюс умножение чисел в экспоненциальной форме и комплексное сопряжение, а так же умножение числа и сопряжённого ему.

Теперь, когда у нас есть два ингредиента, можно сопоставить двум векторам число - 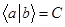. Законы такого сопоставления

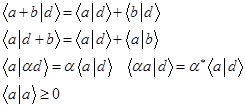
Эти правила не надо пытаться понимать. Они просто вводятся и по сути являются определением скалярного произведения. В дальнейшем эти свойства будут использоваться весьма активно. Скалярное произведение это довольно абстрактная конструкция, и в различных областях математики его определение может отличаться от приведённого здесь. Но геометрически его можно понимать как умножение длин векторов на косинус угла между ними. Можно и так – берём вектор и проецируем на направление, которое он задаёт другой вектор. И дальше умножаем длину первого вектора на длину проекции. Эту сложную словесную конструкцию поясняет рисунок 5.

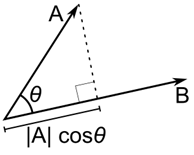
Если вектора перпендикулярны в привычном для нас смысле, то их скалярное произведение равно нулю. Это очень удобно и в дальнейшем изложении будет часто использоваться.

Рис 5. Скалярное произведение

Хотя это можно было бы сделать раньше, но только сейчас мы введём такие понятия как разложение вектора по координатным векторам и линейная комбинация векторов. Такой порядок изложения подчёркивает, что в отличие от школьных времён мы будем умножать вектора не только на действительные числа, но и на комплексные. Такое умножение не будет усложнять дело, но существенно расширит наши возможности. Умножение вектора на комплексное число трудно визуально представить, но это и не надо. Мы уже понимаем, что векторами могут быть не только «школьные» вектора, но и числа, в том числе и комплексные, а сумму чисел «понять» просто. Эти понятия просты и наглядны.

Линейная комбинация – берём несколько векторов, умножаем каждый из них на своё комплексное число и потом складываем получившиеся вектора. Получаем какой- то другой вектор. Это и есть линейная комбинация

Разложение по базисным векторам. Представим себе обычное трёхмерное пространство. В нем можно ввести три взаимно перпендикулярные оси. Вдоль каждой оси отложим вектора определённой длины. Они называются базисными векторами. Не обязательно чтобы вектора были одинаковой длины, но не будет сильным ограничением для дальнейшей теории, если положить что эти вектора имеют единичную длину. Любой вектор пространства можно представить себе как линейную комбинацию этих базисных векторов, а такое представление называют разложением вектора по базису.

Рис 6. Различные базисы. На различие осей можно не обращать внимания.

Для дальнейшего изложения лучше сейчас привести в порядок обозначения и терминологию.

Вектор мы будем обозначать так .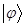

Линейная комбинация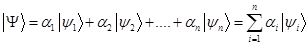

Числа 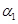…… 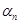называют коэффициентами разложения, а если вектора 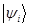базисные, то числа называют координатами вектора в базисе.

Принципиально в пространстве может существовать бесконечно много базисов. И требование взаимной перпендикулярности базисов в общем случае не является обязательным. Но среди всех базисов можно выделить декартовы, т.е. те о которых мы написали изначально – взаимно перпендикулярные оси с отложенными вдоль них единичными векторами. Для квантовой теории такие базисы имеют важное значение, имеющее физический смысл. Как хорошо, что важные элементы теории в то же время являются и простейшими из всех возможных!