Вычисление энтропии

Изобарный процесс (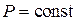). Согласно (5) .

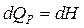Т.к. 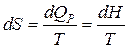, но 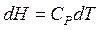, следовательно, .

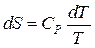Интегрируя, получим:

, . (36)

Под Т₁ подразумевается любая температура, меньшая, чем Т₂.

Интегрирование левой части уравнения (36) можно осуществлять при разных условиях:

1) если теплоемкость не зависит от температуры, тогда результат интегрирования может быть представлен в виде

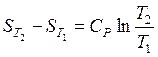или 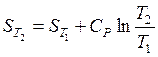. (37)

2) если теплоемкость зависит от температуры и эта зависимость выражается степенным рядом 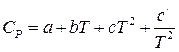, то результаты интегрирования примут вид:

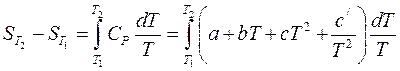_. (38)

Согласно постулату Планка энтропия чистых твердых веществ, образующих идеальные кристаллы, при абсолютном нуле, равна нулю. Учитывая этот постулат, можно определить абсолютное значение энтропии химически чистых веществ в любом агрегатном состоянии и при любых температурах по уравнению:

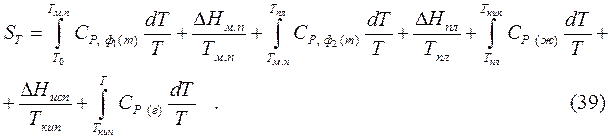
где 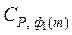– теплоемкость вещества в первой модификации,

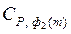– теплоемкость вещества во второй модификации,

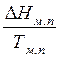- изменение энтропии при модификационном переходе,

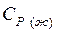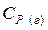, - теплоемкости вещества соответственно в жидком и газообразном состоянии,

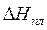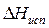, – изменение энтальпии вещества при плавлении и испарении соответственно,

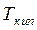, – температуры плавления и кипения вещества.

В общем виде:

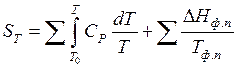(40)

где первая сумма выражает изменение энтропии в процессе нагревания, а вторая изменение энтальпии при фазовых и модификационных переходах.

Для практических расчетов пользуются абсолютными значениями энтропии в стандартном состоянии при 298K, вычисленными при помощи постулата Планка.

Такую энтропию называют стандартной и обозначают . Ее значения приведены в справочнике /5, табл.44; 6, табл.1/. Если T ₁ в уравнении (38) равна 298, то оно принимает вид:

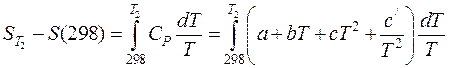(41)

Изменение энтропии в химических реакциях рассчитывают, применяя первое следствие закона Гесса. Например, для реакции :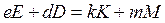

.

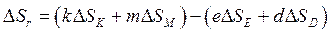Пример 1. Рассчитать энтропию реакции при 473К

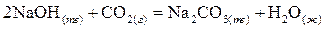
Решение. Для данного расчета, воспользовавшись первым следствием закона Гесса, запишем

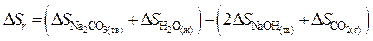
Применяя уравнения (40) и (41), для нашего случая получим:

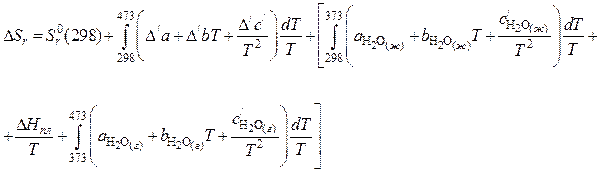
где .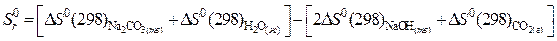

Значение стандартных энтропий веществ находим в справочнике /5, табл.44/:

а) продукты реакции:

;

.

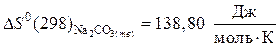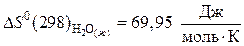б) исходные вещества:

,

.

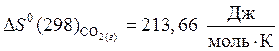и определяем стандартную энтропию реакции:

.

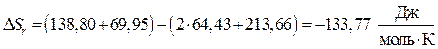Вывод: Изменение энтропии в стандартных условиях для данной реакции равно 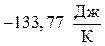, т.е. 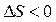, следовательно в прямом направлении (слева направо) в этих условиях реакция не пойдет.

Расчет коэффициентов D^/а, D^/b, D^/c^/ приведен в примере 2 раздела 1.4.2:

;

;

.

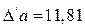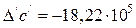Изменение энтропии воды, имеющей в предложенном интервале температур фазовый переход при Т = 373К, будем считать отдельно.

Значения коэффициентов а, b, c¢ для воды в жидком и газообразном состоянии находим в справочнике /5, табл.44/:

; ; ;

, , .

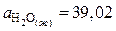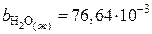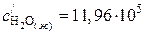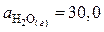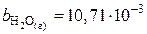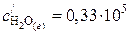Подставив полученные данные в уравнение нашего примера, получим:

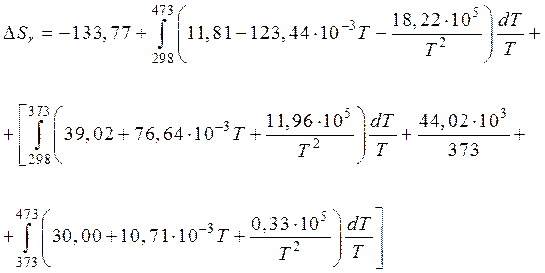
Проинтегрировав, получим

Вывод: . В нашем примере с повышением температуры энтропия возрастает, но ее значение близко к нулю. Это позволяет предположить, что система находится в состоянии, близком к равновесию.

· Изохорный процесс ()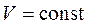

Расчет энтропии в изохорном процессе проводят аналогично расчету для изобарного процесса, только вместо изобарной теплоемкости используется изохорная теплоемкость C_V:

, , .

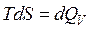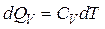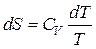Интегрируя в интервале температур 298 - T, получаем:

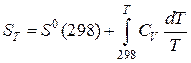. (42)

Если C_V не зависит от температуры, то после интегрирования получим:

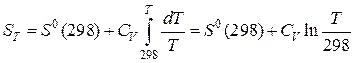. (43)

· Изотермический процесс ()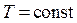

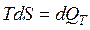Изотермические превращения происходят без изменения внутренней энергии системы (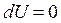), тогда из первого закона термодинамики:

.

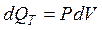Если система подчиняется законам идеального газа, то из уравнения состояния идеального газа Клапейрона - Менделеева:

,

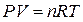где n - количество идеального газа в молях,

R - универсальная газовая постоянная.

В результате подстановки получим:

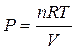, т.е. 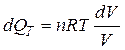, тогда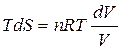

или 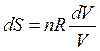(44)

Интегрируем полученное выражение в пределах S₁ - S₂ и V₁ - V₂:

т.е. 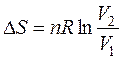(45)

или пользуясь законом Бойля – Мариотта, 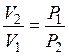, можно записать:

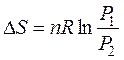(46)

Полученными уравнениями (45) и (46) пользуются для решения задач по изотермическому расширению газов, подчиняющихся законам идеального газа.

Пример 2. Вычислить изменение энтропии при изотермическом расширении 1,7 моля идеального газа, если V₁ = 0,02м³, V₂ = 2м³.

Решение. Для расчета воспользуемся уравнением (45):

.

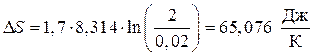Вывод. При изотермическом расширении идеального газа в изолированной системе энтропия возрастает.

Если изотермическим превращением является изменение агрегатного или модификационного состояния вещества при постоянном давлении, то изменение энтропии для одного моля соединения определяется по формуле:

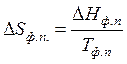, (47)

где 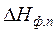- энтальпия фазового или модификационного перехода,

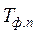- абсолютная температура фазового или модификационногоперехода.

Поскольку энтропия является функцией состояния, то изменение энтропии можно определить, если известно значение параметров начального и конечного состояний системы.

Пусть начальное состояние S₁ характеризуется параметрами T₁ и P₁, а состояние S₂ - параметрами T₂ и P₂ (если за независимые переменные выбраны T и P).Так как изменение энтропии не зависит от пути перехода, то удобнее рассмотреть переход из состояния S₁ в состояние S₂, сначала изменяя температуру от T₁ до T₂ (при 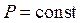), а затем изменяя давление от P₁ до P₂ (при 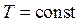). Суммируя изменение энтропии по этим двум процессам, получаем уравнение:

, .

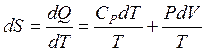После интегрирования получим для системы, содержащей 1 моль идеального газа:

а) если независимые переменные T и P, то

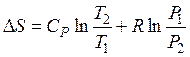; (48)

б) если независимые переменные T и V, то

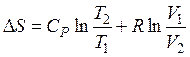. (49)

Пример 3. Найти изменение энтропии при изотермическом сжатии 1 моля паров бензола, при 80⁰С от 0,4053×10⁵ до 1,013×10⁵ Па с последующей конденсацией и охлаждением жидкого бензола до 60⁰С. Нормальная температура кипения бензола 80⁰С; молярная теплота испарения бензола 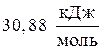; удельная теплоемкость жидкого бензола .

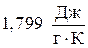Решение. Данный процесс состоит из трех стадий:

1) изотермического сжатия паров бензола от 0,4053×10⁵ до 1,013×10⁵ Па;

2) конденсации паров бензола в жидкость при 80⁰С;

3) охлаждения жидкого бензола от 80 до 60⁰С.

Первая стадия. Процесс изотермический. Изменение энтропии рассчитывается по формуле (46)

.

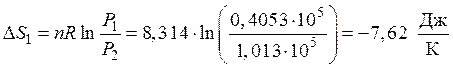Вторая стадия. Фазовый переход - тоже изотермический процесс. Изменение энтропии рассчитывается по формуле (47). Для одного моля бензола

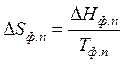, но 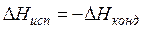, поэтому

.

Третья стадия. Процесс изобарный. Изменение энтропии рассчитывается по формуле (36). По условию задачи идет процесс охлаждения вещества, поэтому для рассматриваемого случая формула (36) примет вид:

,

где 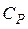- молярная теплоемкость жидкого бензола.

В условии задачи дана удельная теплоемкость 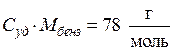, тогда:

.

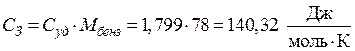Предположим, что молярная теплоемкость жидкого бензола в данных условиях не зависит от температуры.

Подставляя полученные значения C_P и интегрируя в интервале температур , получим:

.

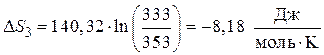Общее изменение энтропии в системе составит:

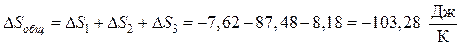
Вывод. Т.к. энтропия убывает, то рассмотренный процесс будет несамопроизвольный, т.е. в изолированной системе он невозможен.

Таким образом, были рассмотрены некоторые уравнения, позволяющие вычислить изменения энтропии по известным изменениям параметров системы и по известным теплоемкостям.

Ранее подчеркивалось, что энтропия применяется как критерий направленности процесса только для изолированных систем, что затрудняет применение её на практике, где многие технологические процессы протекают или при постоянном давлении и температуре в открытых реакторах, или при постоянном объеме и температуре в закрытых реакторах. Однако с помощью энтропии можно вычислить другие функции, которые могут выступить в роли критерия равновесия и направленности процесса. К таким функциям относятся энергия Гельмгольца (изохорно-изотермический потенциал) и энергия Гиббса (изобарно-изотермический потенциал).