Механический эквивалент теплоты

В прежние времена, когда природа теплоты еще не была понята, теплоту измеряли в особых единицах – калориях, за которую принималось количество теплоты, необходимой для нагревания одного грамма воды на один градус Цельсия.

В статье “Замечания о силах неживой природы”, появившейся в мае 1842 года в журнале “Анналы химии и фармакологии”, врач Юлиус Роберт Майер (1814-1878) приводит вычисление механического эквивалента теплоты (что для нас означает перевод джоулей в калории, хотя во времена Майера были другие единицы измерения работы). Хотя Майер получил заниженное численное значение коэффициента перевода, поскольку в его распоряжении не оказалось правильных экспериментальных данных, однако ход его рассуждений был принципиально верным. Поэтому, следуя идее Майера и опираясь на более точное знание разности удельных (в расчете на единицу массы) теплоемкостей воздуха при постоянном давлении и постоянном объеме (С_р - С_v), проделаем следующий мысленный эксперимент: При нагревании на один градус Кельвина одного кубического метра воздуха при постоянном давлении в нормальных условиях (Р = 10⁵ Па и Т = 273 К) согласно закону Гей-Люссака его объем увеличится на 1/273 часть, то есть DV = 1/273 м³. Плотность воздуха при нормальных условиях r = 1,29 кг/м³. Разность удельных теплоемкостей (С_р - С_v) = 68 калорий/кг·К согласно современным данным.

Уже во времена Майера было понятно, что превышение теплоемкости при постоянном давлении над теплоемкостью при постоянном объеме связано с работой газа по увеличению объема в условиях противодействия внешнего давления расширению газа. Следовательно, должно выполняться соотношение

rV(С_р - С_v)∙DТ = Р∙DV,

так как избыточное потребление теплоты (по сравнению с изохорным процессом) идет на совершение работы.

В нашем случае это равенство дает численное соотношение

1,29∙1∙68∙1 (калории) = 10⁵∙1/273 (Дж),

из которого сразу следует, что 1калория = 4,19Дж, или 1Дж = 0,24 калории, что и представляет собой механический эквивалент теплоты и термический эквивалент работы.

Итак, когда затрачивается теплота и совершается работа (и, соответственно, когда затрачивается работа и обнаруживается теплота), то эти величины друг другу пропорциональны. Именно в этом состоит принцип эквивалентности теплоты и работы.

Как мы видим, Майер использовал очень остроумный способ вычисления коэффициента пропорциональности теплоты и работы с помощью мысленного эксперимента и опытных данных о свойствах газов, но были, конечно, и прямые опыты по вычислению механического эквивалента теплоты. Так, Джоуль на протяжении тринадцати лет совершенствовал устройство своего термостата (конструкция которого рассматривается во многих учебниках), в котором работа, затраченная на перемешивание жидкости с помощью опускающихся тяжелых грузов, вызывала повышение температуры этой жидкости. Само собой разумеется, что все правильно поставленные опыты дают не противоречащие друг другу результаты, то есть совпадающие в пределах погрешности опыта.

Еще один результат, полученный Майером, весьма пригодился в модели идеального газа. Поскольку внутренняя энергия реальных газов согласно экспериментам Гей-Люссака (оказавшимися впоследствии недостаточно точными) не показала зависимости от объема (то есть внутренняя энергия газа зависит как будто бы только от температуры), то из уравнения состояния идеального газа (1.2') и выражения (2.6) получается соотношение Майера для разности молярных теплоемкостей идеального газа

С_р - С_v = R, (2.8)

где R = 1,98 калории/мольК = 8,31 Дж/мольК - универсальная газовая константа.

3. МОДЕЛИРОВАНИЕ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ. РОЛЬ МОДЕЛИ ИДЕАЛЬНОГО ГАЗА

3.1. Уравнение состояния и особенности моделирования в термодинамике. Термодинамические уравнения состояния. Обратимые и необратимые процессы. Роль квазистатических процессов. Термодинамические циклы

Вид уравнения состояния (1.1) (называемого иногда термическим уравнением состояния), связывающего термодинамические параметры, можно выяснить только из опытных данных. Для большинства веществ уравнение состояния нам неизвестно в силу огромной сложности этой связи (особенно для жидкого агрегатного состояния). Как преодолеть эту трудность? Как поступают в такой ситуации в термодинамике?

Очень важным в термодинамическом подходе является следующее.

Чтобы производить в термодинамике полезные в техническом отношении вычисления, совсем не обязательно знать именно термическое уравнение состояния, которое, как правило, неизвестно или оказывается чрезмерно сложным. Вместо этого, оказывается, достаточно знать некоторые функции состояния термодинамической системы, выражаемые через макроскопические параметры, и связи между этими функциями. Знание даже одной из таких функций позволяет через общие для любых тел термодинамические соотношения (смотрите 7.3), найти остальные интересующие нас функции. Это возможно потому, что законы движения энергии в тепловой форме одни и те же для всех тел, независимо от их конкретных термических уравнений и агрегатных состояний. Поэтому оказалось возможным изучать тепловые закономерности, в силу их независимости от агрегатных состояний, с помощью такого удобного для изучения объекта как сильно разреженный газ. В предельном случае мы получаем такой идеализированный (реально в природе не существующий) объект изучения как идеальный газ. Преимущества оперирования с таким объектом очевидны – предельно простое, уже известное нам термическое уравнение состояния (1.2), позволяющее сравнительно просто получить эти всеобщие термодинамические уравнения состояния.

Еще раз напомним, что все функциональные связи, о которых здесь идет речь (и которые еще предстоит найти с помощью модели идеального газа), существуют только при термодинамическом равновесии или незначительных (пренебрежимо малых) отклонениях от него. Процессы, идущие при незначительных отклонениях от состояния равновесия, называются равновесными или квазистатическими. Они могут идти как в одну, так и в другую сторону, то есть являются полностью обратимыми. Термодинамика («термостатика») не занимается вопросами скоростей выравнивания термодинамических параметров (этим занимается физическая кинетика), а только вопросами равновесных состояний или достаточно близких к ним. Рассматриваемые здесь квазистатические процессы суть последовательности равновесных состояний при переходе термодинамической системы из начального равновесного состояния в конечное состояние, также равновесное. Хотя в интересующих практику вопросах квазистатические процессы реально не встречаются, но для термодинамических расчетов они важны, так как здесь существенным, принципиальным моментом является не их замедленность, а их обратимость.

В термодинамике обратимыми считаются такие процессы, посредством которых термодинамическую систему можно вернуть в исходное состояние так, чтобы после выполнения процесса во внешних телах не произошло никаких изменений. При этом не обязательно, чтобы система на обратном пути проходила все промежуточные состояния, пройденные на прямом пути.

Таким образом, квазистатические процессы моделируют любые обратимые процессы по их результатам.

Кроме того, в термодинамике для расчетов используется тот факт, что все начальные и конечные состояния можно считать равновесными. Следовательно, можно не считаться с тем, каким образом система шла из начального состояния в конечное состояние (обратимым или необратимым). А вычислять изменение функций состояния системы можно по обратимому переходу системы из одного состояния в другое так, как если бы процессы шли квазистатическим образом (когда справедливы уравнения состояния и, значит, их можно использовать для вычисления изменений любых интересующих нас функций состояния).

Понятие обратимости является весьма важным для термодинамики, где все процессы четко подразделяют на процессы обратимые и необратимые. При обратимости не имеет значения для окончательного результата способ перевода термодинамической системы из одного состояния в другое, то есть, если в результате кругового процесса система возвращается в первоначальное состояние (совершает цикл), то и в окружающих телах никаких изменений не происходит. Если в механике все процессы предполагаются принципиально обратимыми, то в термодинамике, например, нагревание тел при их торможении силами трения необратимо, так как нельзя посредством охлаждения привести эти тела в движение и вообще вернуть в первоначальное состояние обратимым образом.

В технических приложениях термодинамики весьма важна роль циклических процессов, так как тепловые машины используются для циклического преобразования энергии хаотического движения микрочастиц в механическую энергию макроскопических тел. Если задаться целью детального исследования циклов, то надо знать все промежуточные состояния, непосредственное изучение которых не всегда возможно хотя бы потому, что термодинамика утверждает существование уравнений состояния только для равновесных состояний. Выход из затруднения дает существование (хотя бы теоретическое) обратимых процессов, для которых пути системы из начального состояния в конечное и, следовательно, все промежуточные состояния, не играют никакой роли. Значение имеют лишь различия в начальном и конечном (равновесных) состояниях.

Поскольку реальный путь перехода системы из одного состояния в другое проследить не удается, поскольку неизвестно как быть с термодинамическими параметрами в неравновесных промежуточных состояниях, то реальный переход моделируется (мысленно заменяется) бесконечно медленным (и поэтому обратимым) квазистатическим переходом из начального состояния в конечное. При таком переходе система все время остается в состоянии термодинамического равновесия, и, следовательно, все время можно говорить о существовании уравнения состояния. При этом сравнительно легко просчитываются изменения любых функций состояния, а по ним вычисляются представляющие практический интерес термодинамические характеристики.

С другой стороны, быстропротекающие (скорость изменения внешних условий велика по сравнению со скоростью реакции, то есть быстротой релаксации системы), и в силу этого обратимые (не в строгом смысле) процессы сродни квазистатическим. Поэтому квазистатические процессы являются хорошей моделью столь быстрых процессов, когда необратимость не успевает проявить себя, так как не успевает произойти заметного выравнивания интенсивных термодинамических параметров. Таким образом, только кажется, что в природе редко осуществляются почти обратимые процессы. На самом деле, поскольку все необратимые процессы требуют времени для своего осуществления и характеризуются временем релаксации, и если процесс происходит настолько быстро, что система не успевает “срелаксировать”, то процесс практически обратим, поскольку длительность процесса много меньше времени релаксации. Но поскольку общие свойства обратимых процессов можно изучать на частном случае процессов, протекающих столь медленно, что систему можно считать все время находящейся в состоянии теплового равновесия (когда все термодинамические параметры связаны через уравнение состояния), то квазистатические процессы оказываются моделью любых обратимых, в том числе и быстропротекающих, процессов. Именно в этом и состоит смысл рассмотрения бесконечно-медленных процессов (на практике никогда не реализуемых), именуемых квазистатическими процессами.

Необратимыми процессами являются все процессы самопроизвольного перехода термодинамических систем из неравновесного состояния в состояние равновесное. Они не обязательно связаны с наличием макроскопических движений, но если таковые присутствуют, то после их прекращения под влиянием сил трения, кинетическая энергия этих макроскопических движений переходит в энергию хаотических микродвижений (энергию движений микроскопических частиц), которая распределяется по всему объему системы. Происходит диссипация, то есть рассеяние энергии, распределение её по микрообъектам.

3.2. Модель идеального газа. Уравнение состояния идеального газа. Идеальный газ в силовом поле. Барометрическая формула

Итак, термодинамика и статистическая механика с разных позиций изучают одно и то же, а именно – влияние на поведение макроскопических объектов (при передаче энергии не силовым, а тепловым способом) закономерностей, порожденных неупорядоченностью расположения и несогласованностью движения микрочастиц, образующих термодинамическую систему. Определенные предположения или гипотезы, положенные в основу этих дисциплин, отличаются друг от друга, хотя они и являются обобщением одних и тех же наблюдаемых макроскопических явлений. Так, статистическая механика базируется на положениях, относящихся к гипотезам о строении и взаимодействии на микроуровне молекул вещества конкретных природных тел. Благодаря более глубокому проникновению в микроструктуру изучаемых конкретных макрообъектов статистическая механика позволяет более детально предсказывать их поведение в термодинамических процессах, но не обладает всеобщностью выводов феноменологической термодинамики. В свою очередь, термодинамика позволяет получить более глубокое, чем просто макроскопически-описательное обоснование и истолкование наблюдаемых закономерностей, опираясь, именно в силу всеобщности изучаемых ею закономерностей, на рассмотрение микроструктуры не реальных (что в принципе возможно, но связано с резким усложнением математических выкладок), а идеализированных макроскопических объектов, расчет поведения которых не требуют сложной математики. Полученные на основе изучения поведения таких идеализированных объектов (моделей) общие закономерности (общие для всех объектов как идеальных, так и неидеальных, как простых, так и сложных) оказываются не только легко постигаемыми в своих принципиальных моментах, но и весьма полезными в технических приложениях.

Сначала рассмотрим самую простую модель термодинамической системы – идеальный газ. В модель идеального газа заложено два основных предположения: первое – о невзаимодействии молекул газа на расстоянии (взаимодействие осуществляется только в пренебрежимо краткое по сравнению со временем полета время соприкосновения), и второе – о возможности пренебрежения собственным объемом молекул по сравнению с полным объемом, занимаемым газом. Эта модель хорошо себя оправдывает в случае достаточно разреженных газов, когда диаметр молекул много меньше среднего расстояния между ними. Разумеется, применимость модели идеального газа не безгранична, и имеется достаточно много явлений (например, фазовые превращения – переход из одного агрегатного состояния в другое), для анализа которых даже на качественном уровне модель идеального газа непригодна и, значит, в этих случаях следует обращаться к более сложным моделям. Однако для решения поставленной задачи – обнаружения фундаментальных термодинамических соотношений (термодинамических уравнений состояния) – модель идеального газа оказалась вполне пригодной.

Уравнение состояния идеального газа нам дает объединенный газовый закон (1.2), который в расчете на один моль принимает вид

РV = RT (3.1)

В термодинамике принято все вычисления проводить в расчете на один моль вещества, что и будет подразумеваться, если специально не оговаривается другое количество вещества, поэтому число молей n = m/M нами всегда будет считаться равным единице.

Уравнение (1.2) для произвольного числа молекул N иногда записывают в виде

PV = NkT, (3.2)

где k – постоянная Больцмана (R =N_A·k).

Это уравнение может быть получено из рассмотрения упругих ударов молекул идеального газа о стенки сосуда (газ в «ящике»). Такой способ получения уравнения является задачей статистической механики (см. ПРИЛОЖЕНИЕ 1). Уравнение (3.2) можно также переписать в виде

Р = nkT, (3.3) где n – концентрация молекул (N/V).

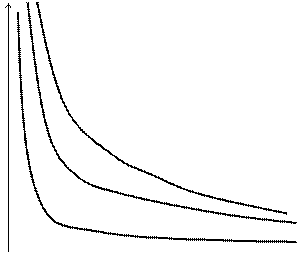
Уравнение состояния идеального газа хорошо иллюстрируется геометрически. Так как в уравнение входят только три переменные, то любые две из них можно выбрать в качестве переменных, откладываемых по осям прямоугольной системы координат на плоскости, и при любом фиксированном значении третьей переменной уравнение состояния даст некоторую линию на плоскости. Так, задаваясь различными значениями температуры Т₁,Т₂,Т₃,.., получаем для идеального газа семейство кривых, различающихся значениями параметра Т и называемых изотермами. В случае идеального газа кривая, получающаяся при постоянной температуре Т = Const, представляет собой равнобочную гиперболу на плоскости (Р,V). Изменяя значение параметра Т, мы получаем семейство гипербол, называемых изотермами идеального газа.

На рисунке 1 представлено семейство изотерм, описываемых уравнением (3.1).

Р

Т₃

Т₂

V₁ V₂ V

Рис.1. Изотермы идеального газа. Т₃ > T₂ > T_1.

Воспользуемся моделью идеального газа, чтобы рассмотреть как изменяется с изменением координаты давления газа, находящегося в однородном силовом поле, считая атмосферу газа изотермической. Пусть внешнее силовое поле направлено вдоль оси z, например, сверху вниз (смотрите рис. 2), а потенциальная энергия одной молекулы в этом поле равна u. Тогда сила, действующая на одну молекулу f = -du/dz (или fdz = - du), а малое изменение давления газа dp при смещении на расстояние dz находится как отношение суммарной силы F, действующей на все молекулы внутри некоторого малого объема dV = Sdz, к площади S, то есть изменение давления газа на малом расстоянии dz равно dp = F/S = ndV·f /S = ndz·f = - ndu.

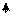
z

P(z + dz) = P + dp

dz

P(z)

S

Рис.2.

Используя уравнение состояния идеального газа (3.3) и считая температуру газа постоянной, имеем dp = dn·kT, что позволяет сразу получить соотношение dn/n = - du/kT, интегрируя которое получаем формулу Больцмана

n = n_o exp (- u/kT), (3.4)

показывающую распределение молекул газа в силовом поле. Здесь n_o - концентрация молекул на уровне нулевого значения потенциальной энергии.

Чтобы получить из уравнения (3.4) зависимость давления воздуха от высоты местности (предполагая постоянство температуры) надо вспомнить, что n = P/kT, а u = m₁gh, где m₁ - масса одной молекулы, g - ускорение силы тяжести, h - высота, и тогда давление P = P_oexp (- m₁gh/kT). Теперь, умножая числитель и знаменатель в показателе экспоненты на число Авогадро, и помня, что m₁N_A = M (масса моля), а kN_A = R (газовая постоянная), получаем барометрическую формулу

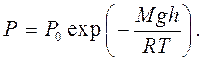(3.5)

Закон распределения частиц в поле силы тяжести был использован французским ученым Жаном Перреном (1909г) для наиболее точного (для своего времени) экспериментального определения числа Авогадро.

3.3. Изотермические и адиабатные процессы

Date: 2015-05-09; view: 1535; Нарушение авторских прав