Властивості ЛП

1) 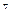лін.прост.має єдиний нульовий Θ.

_▲Нехай 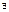Θ₁ є L, Θ₁-нульов.вектор.Тоді Θ+ +Θ₁=Θ₁.З іншого боку Θ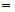+ +Θ₁=Θ Θ₁=Θ_▲

2) 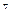вектор простору L має єдиний протилежний

_▲Нехай для х є L 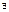х₁ і х₂ є L:х+х₁=Θ і х+х₂=Θ. Віднімемо: х₁-х₂=Θ 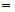х₁=х_2▲

3) 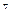α є Р: α·Θ=Θ.

_▲α·а=α(а+Θ)=αа+αΘ 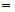αа=αа+αΘ; αΘ=Θ._▲

4) 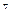α≠Θ 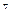х≠Θ αх≠Θ

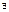
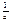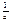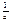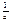_▲Нехай αх=Θ і α≠Θ,х≠Θ. Так як α є Р,α≠0,то . Помножимо першу рівність на : αх= Θ 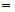х=Θ(3а 3))

що суперечить умові_▲

5) 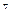х є L і 0 є Р:0·х=Θ

_▲Θх=0х-Θ 0х=Θх+Θ= =0х+(х-х)=0х+х-х = =(0+1)х-х=Θ_▲

6) Якщо α≠β і х≠Θ,то αх≠βх

_▲Припустимо що αх=βх за умови,що α≠β і х≠Θ. Розглянемо різницю лівої і правої частин: αх-βх=Θ.

(α-β)х=Θ 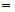(α-β)=0 або х=Θ.α=β, а це суперечить умові_▲

С-ма векторів а₁,а₂,…а_m простору L назив. лінійнонезадежною, якщо їх лінійна комбінація дор. нуль вектору,лише за умови, що всі λ_і =0.

λ₁а₁+λ₂а₂+…+λ_mа_m=Θ,

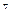λ_і =0.

С-ма векторів а₁,а₂,…а_m простору L назив. лінійнозалежною, якщо її комбінація є нуль вектором при умові,що хочаб 1 з λ_і ≠0,т.б. 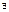λ_і ≠0:

λ₁а₁+λ₂а₂+…+λ_mа_m=Θ.

Властивості лінійної залежності та лінійної незалежності векторів:

1.С-ма векторів ЛЗ 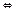,коли хочаб 1 з її векторів лінійно виражається через інші.

Д-ня: S={a₁, a₂,…,a_m}

1. Необхідність. Нехай S – ЛЗ, тоді у рівності 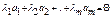хоча б одне з 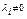. Нехай це, наприклад,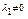

Тоді:

отже, лінійно виражається через інші.

2. Достатність.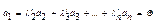

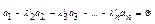
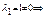система векторів ЛЗ. Властивість доведено.

2.Якщо с-ма має нуль вектор,то вона ЛЗ.

Доведення. Нехай в системі S={a₁, a₂,…,a_m} вектор .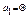

Розглянемо лінійну комбінацію:

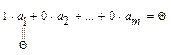
І оскільки 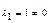, то S – ЛЗ. Властивість доведено.

3.С-ма,що містить 2 колінеарні вектори- ЛЗ.

4.Якщо підсистема с-ми векторів ЛЗ,то і вся с-ма ЛЗ.

Доведення: Нехай S={a₁, a₂,…,a_m} – задана система векторів і

S′={a₁, a₂,…,a_k} – її ЛЗ підсистема .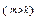

Тоді існує ненульова лінійна комбінація векторів системи S′, яка дорівнює θ.

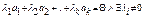
Розглянемо лінійну комбінацію векторів системи S:

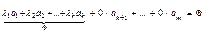
Причому знайдеться .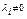

Отже, система S – ЛЗ. Властивість доведено.

5.Якщо с-ма ЛНЗ,то і 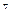її підсистема також ЛНЗ.

Доведення: Припустимо, що система S містить хоча б одну ЛЗ підсистему, але тоді за властивістю 4, с-ма S також повинна бути ЛЗ, що суперечить умові. Отже, припущення невірне. Властивість доведено.

6.Нехай задано 2 с-ми векторів:S={ а₁,а₂,..а_m} і Т={b₁,b₂,..,b_k}, причому m>k. Якщо всі вектори с-ми S лінійно виражаються через вектори с-ми Т, то с-ма S- ЛЗ.

Наслідок: у n-вимірному просторі будь-яка с-ма, що містить більш ніж n векторів, є ЛЗ.(без д-ня)

Нехай маємо систему S={a₁, a₂,…,a_m}, де

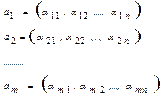
Ведучою компонентою вектора наз. його першу зліва координату, відмінну від 0.

Нехай вектори a₁, a₂,…,a_m мають ведучі компоненти 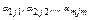відповідно. Тоді с-му цих векторів наз. ступінчатою, якщо кожна наступна компонента знаходиться правіше від попередньої, тобто .

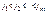У випадку, коли m=n і 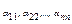- ведучі компоненти векторів a₁, a₂,…,a_n відповідно, то с-му цих векторів наз. діагональною.

7. Ступінчата, зокреме діагональна с-ма векторів ЛНЗ.

n-вимірним векторним простором назив.простір L у якому існує с-ма з n ЛНЗвекторів, а 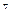с-ма векторів цього простору, що містить > n векторів є ЛЗ.При цьому L назив. скінченно вимірним простором і познач. L_n (Lⁿ), а число n-його розмірністю і познач.n=dim L_n.

Приклади: (С,+,R)-дійсний простір комплексних чисел; множина многочленів від 1-ї змінної з дійсними коефіцієнтами степеня < або = n утворює дійсний лін.простір розмірності (n+1);Р[х] над Р; Р(х) над Р; М_n(Р) над Р; Д³.

Рангом ненульової с-ми є максимальна к-сть незалежних векторів в ній.

Базисом простору L назив. ЛНЗ с-ма векторів цього простору, через які лінійно вираж. кожен вектор цього простору. {е₁,е₂,…е_n}-Bas L_n 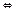{е₁,е₂,…е_n}-ЛНЗ с-ма і 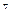х є L х= α₁е₁+…+α_nе_n. Коефіц. α₁,…,α_n у цьому розкладі назив. координатами вектора х у цьому базисі.

Т-ма. Довільний вектор простору виражається через базисні однозначно.

_▲Нехай 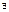2 розклади вектору:

х= α₁е₁+α₂е₂+…+α_nе_n і

х= β₁е₁+β₂е₂+…+β_nе_n. Віднімемо: (α₁-β₁)е₁+(α₂-

-β₂)е₂+…+(α_n-β_n)е_n=Θ. Оскільки{е₁,е₂,…е_n}-ЛНЗ с-ма,то остання рівність виконується лише за умови α₁-β₁=0, α₂-β₂=0, …, α_n-β_n=0 або α₁=β₁, α₂=β₂, …, α_n=β_n.Т.б. розклад вектора через базис-однозначний._▲

Т-ма (Критерій базису):

Підсистема S′ с-ми S є базисом цієї с-ми 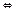коли S′ максимальна ЛНЗ підс-ма с-ми S.

Наслідок: базисом ЛНЗ с-ми є вона сама.

Т-ма: Лінійний простір L є n-вимірним 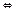коли він має базис з n векторів.

_▲ Необхідність. Нехай L-n-вимірний векторний простір.Тоді він містить n-ЛНЗ векторів: а₁,а₂,…а_n. Причому 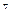вектор х є L, с-ма

{х,а₁,а₂,…а_n}- ЛЗ.

Це означає,що існує не нульова лінійна комбінація цих векторів, що рівна Θ. λх+λ₁а₁+…+λ_nа_n=Θ (1).

Доведемо,що λ≠0. Припустимо супротивне: λ=0,тоді λ₁а₁+…+λ_nа_n=Θ і так як вектори а₁,а₂,…а_n-ЛНЗ,то λ_і=0 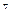і=1,..,n. Таким чином с-ма {х,а₁,а₂,…а_n}-ЛНЗ, що суперечить умові. Отже λ≠0. Перенесемо у рівності (1) всі доданки починаючи з другого вправо, та поділимо обидві частини на λ:

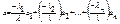
т.б. вектор х розкладається через а₁,а₂,…а_n.Отже {а₁,а₂,…а_n}-Bas L.

Достатня. Нехай простір L містить базис {а₁,а₂,…а_n}.Покажемо що L- n-вимірний.Так як базисні вектори ЛНЗ і кожен вектор х є L лінійно вираж. через базис, то с-ма {х,а₁,а₂,…а_n}-ЛЗ і за означенням L-n-вимірна._▲

Наслідок1.

В n-вимірному просторі будь-яка с-ма, що складається з лін. незалеж. векторів – є базисом.

_▲Нехай простір L n-вимірний і {а₁,а₂,…а_n}- с-ма ЛНЗ векторів.Покажемо,що ця с-ма є базисом.За означ. N-вимірного простору. Для вектора х є L с-ма

{х,а₁,а₂,…а_n}-ЛЗ і за т-мою х=λ₁а₁+…+λ_nа_n,т.б.

Кожен вектор простору лінійно виражається через вказану с-му векторів,а значить вона є базисом._▲

Наслідок2.

Будь-які 2 базиси n-вимірного простору містять однакову кількість векторів.

Т-ма: Будь-яку ЛНЗ с-му векторів n-вимірного простору можна доповнити до базису цього простору.

_▲Нехай {а₁,а₂,…а_m}-ЛНЗ с-ма простору L_n.1.Якщо m=n, то ця с-ма і є базисом L_n.

2.Нехай m<n.За означ.n-вимірного простору, знайдеться вектор а_m+1 {а₁,а₂,…а_m, а_m+1 }-ЛНЗ с-ма.m+1=n,то остання с-ма є базисом L_n.В іншому випадку процес можна продовжити далі. Через скінчену кількість кроків одержимо с-му ЛНЗ векторів, яка і є базисом._▲

Date: 2015-04-23; view: 810; Нарушение авторских прав