Основные теоретические сведения для выполнения

Для определённой в некоторой окрестности точки 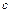функции 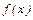число 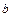называется пределом функции 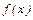, если при 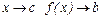. При этом пишут:

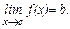
Если 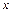при стремлении к 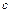принимает только значения, меньшие 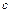,то пишут:

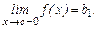
и 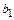называют пределом функции 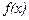в точке с слева.

Если 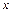при стремлении к 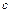принимает только значения, большие 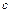,то пишут:

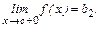
и 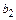называют пределом функции 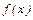в точке с справа.

Функция непрерывна в точке 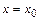,если выполняется равенство:

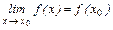(1)

При нахождении предела 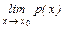некоторой функции p(x) (x₀- конечное число или 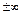) возможно появление неопределённостей типа:

.

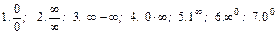Неопределенности типа 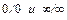могут быть раскрыты по правилу Лопиталя:

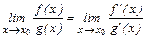, (2)

которое можно применять, пока существует неопределенность первого или второго типа. (Понятие производной будет дано ниже).

Неопределённости типа 3-7 тождественными преобразованиями могут быть сведены к неопределенностям 1-ого или 2-ого типа.

Пример 1. Найти предел .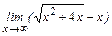

Имеем неопределённость 3-го типа. Умножив и разделив выражение на сопряжённое, получим неопределенность 2-го типа, которую легко раскрыть:

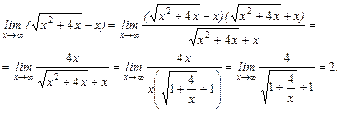
При нахождении пределов часто используются первый и второй замечательные пределы:

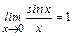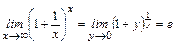1) ; 2) . (3)

Пример 2. Найти предел .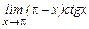

Имеем неопределённость 4-го типа. Применяя правило Лопиталя, найдём предел:

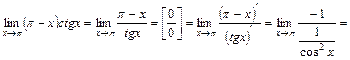
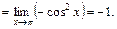
Пример 3. Найти предел: .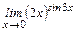

Имеем неопределенность 7-го типа. Обозначим искомый предел через А и прологарифмируем обе части равенства. Получим:

.

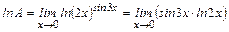В правой части равенства имеем неопределенность 4-го типа. Преобразуем ее в неопределенность 1-го типа и раскроем по правилу Лопиталя:

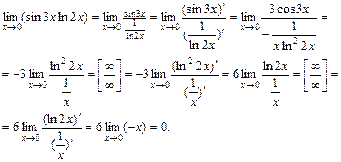
Т.о. 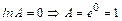, т.е. искомый предел равен 1.

Аналогично могут быть раскрыты неопределенности 5-го и 6-го типов.

Производной функции 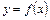называется предел отношения приращения функции 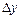к приращению аргумента 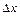, когда 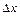стремится к 0:

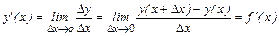. (4)

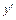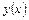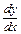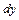Кроме для производной функции используются также обозначения , где и 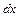называются соответственно дифференциалом функции 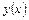и дифференциалом аргумента 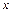. Дифференциалом первого порядка функции 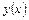называется та часть приращения функции при приращении аргумента 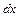, которая линейно зависит от 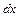. Т.о., по определению дифференциал функции 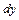равен произведению её производной на дифференциал аргумента : .

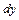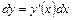Геометрически производная функции в точке x представляет собой тангенс угла наклона касательной к положительному направлению оси Ox: 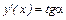. Т.к. производная характеризует скорость изменения функции при изменении аргумента, то физический смысл производной по времени от вектора перемещения – скорость 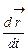. Производная по времени от скорости – ускорение .

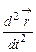Операция нахождения производной функции называется дифференцированием функции.

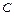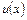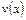Если – константа, а и – дифференцируемые функции, то справедливы следующие правила дифференцирования:

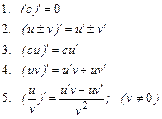
6. Если 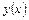сложная функция от 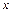, т.е. у = у[р(х)], где у(р) и р(х) – дифференцируемые функции, то 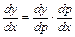или

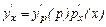. (5)

Используя формулу (4) для производной функции и правила дифференцирования, можно получить таблицу производных основных элементарных функций:

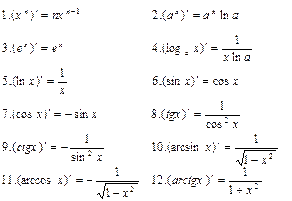
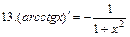
Производную сложной показательной функции 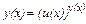легко найти, предварительно прологарифмировав обе части равенства. В результате получим:

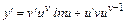. (6)

Производная от первой производной функции 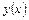обозначается 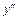или 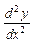и называется производной 2-го порядка или второй производной.

Производной n-го порядка функции 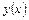, если она существует, называется производная от производной (n-1)-го порядка и обозначается 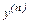или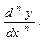

Если функция 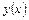задана неявно и определяется уравнением 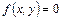, то дифференцируя обе части равенства по 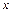получим уравнение первой степени относительно 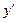, из которого найдём 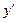, как некоторую функцию от 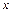и : .

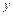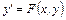Дифференцируя по 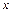обе части последнего равенства и используя выражение для 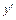, можно получить выражение для второй производной .

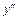Пример 4.

Найт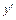и и 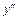, если 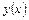задано неявно уравнением .

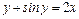Приведём уравнение к виду .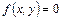

;

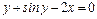продифференцировав, получим:

(а) .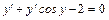

Откуда

(б) .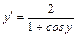

Продифференцируем по 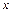обе части равенства (а):

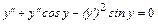
(в) .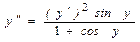

Подставляя в (в) 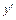из (б) получим:

.

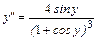Если функция 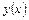задана в параметрическом виде 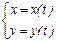, то производные определяются формулами:

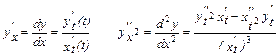(7)

Пример 5.

Найти 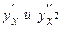, если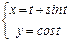

Используя формулу (7) получим:

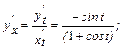
Если существуют производные любого порядка функции 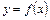, то функция 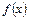может быть записана в виде

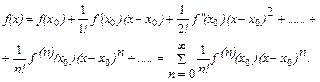(8)

где под знаком суммы производная нулевого порядка 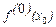принимается равной 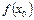; n!= 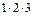...n; 0!=1. Формула (8) называется формулой Тейлора разложения функции 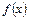в точке 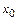по степеням 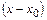. При этом предполагается, что правая часть формулы (8) должна быть ограниченной функцией от .

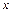При 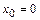из (8) получим:

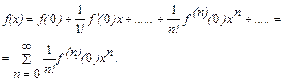(9)

Формула (9) называется формулой Маклорена разложения функции 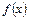в точке 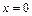по степеням .

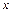Пример 6.

Разложить функцию 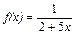по формуле Тейлора в точке .

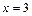Вычисляем производные функции 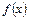и увидев закономерность, запишем выражение для производной n-го порядка :

.

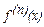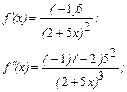
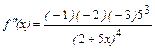Легко увидеть, что 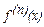имеет следующий вид:

.

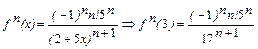Подставляя 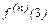в формулу (9), получим:

.

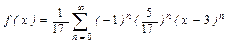Date: 2015-06-08; view: 682; Нарушение авторских прав