Приложения алгебры логики

6.1. Формализация высказываний.

Высказывание - это утверждение об объектах, выраженное повествовательным предложением. Это предложение имеет однозначный смысл и о нем можно точно сказать истинно оно или ложно. Примеры высказываний:

1) 4 × 3 =12.

2) sin x > 1.

3) Лондон - столица Франции.

4) Дон впадает в Азовское море.

Высказывания 1), 4) истинны, а высказывания 2), 3) ложны. Элементарными (простыми) называются высказывания, которые сообщают единичный факт. Сложные высказывания образуются из простых с помощью логических операций, рассмотренных ранее: отрицания, конъюнкции, дизъюнкции, импликации и других. Пусть p и q обозначают высказывания:

p: Петр водитель автомобиля;

q: Анна учится в ДГТУ;

r: Петр- летчик.

Сложное высказывание «Петр водитель автомобиля и Анна учится в ДГТУ» состоит из двух частей, объединенных связкой «и». Символически это высказывание записывается в виде p Ù q (p и q). Высказывание «Петр водитель автомобиля или Петр- летчик» символически выражается как p Ú r (p или r).

Отрицание или опровержение высказывания p обозначается Ø p или .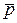

Высказывание Ø q утверждает, что «Анна не учится в ДГТУ». Комбинация выше перечисленных связок приводит к более сложным высказываниям. Если s это высказывание «Денису нравится информатика», то высказывание «Петр не водитель автомобиля, Анна учится в ДГТУ и Денису нравится информатика» символически записывается как Ø p Ù q Ù s. Высказывание «Анна учится в ДГТУ, Петр- не летчик и Денису не нравится информатика» формализуется формулой q ÙØ r Ù Ø s.

Условные высказывания вида «если p то q» выражаются импликацией p® q. Например, предложение «Если Николай сдаст все экзамены без троек, то он получит стипендию» выражается импликацией p ® q, где p- высказывание «Николай сдаст все экзамены без троек», q- высказывание «он получит стипендию». Напомним, что импликация p ® q равносильна формуле

Ø p Ú q, т.е. утверждение «если p то q» означает «не p или q». Учитывая таблицу истинности для импликации, утверждение «Если Николай сдаст все экзамены без троек, то он получит стипендию» истинно даже в том случае, когда соответствующие p и q ложны или p ложно, а q истинно.

С условным высказыванием p ® q связаны еще три типа высказываний: конверсия, инверсия и контрапозиция высказывания p ® q. Они определяются следующим образом:

q ® p конверсия высказывания p ® q;

Ø p ® Ø q инверсия высказывания p ® q;

Ø q ® Ø p контрапозиция высказывания p ® q.

Рассмотрим высказывание «если она играет на скрипке, то он кричит». Для этой импликации получаем:

конверсия: «если он кричит, то она играет на скрипке»;

инверсия: «если она не играет на скрипке, то он не кричит»;

контрапозиция: «если он не кричит, то она не играет на скрипке». Конверсию q ® p называют высказыванием обратным данному p ® q; инверсию Ø p ® Ø q - противоположным высказыванием для высказывания

p ® q; контрапозиция - это обратное противоположное высказывание для исходного утверждения. Легко видеть, что импликация и контрапозиция имеют одну и ту же таблицу истинности, т.е. логически эквивалентны. Контрапозиция условных высказываний имеет в математике большое значение. Часто теорему легче доказать от противного, чем дать ее прямое доказательство. Однако импликация и ее конверсия (или инверсия) имеют различные таблицы истинности, игнорирование этого факта приводит к ошибкам в логических рассуждениях.

Утверждения «p эквивалентно q», «p необходимое и достаточное условие q», «p тогда и тогда, когда q» символически записываются с помощью связки эквивалентность (~) p ~ q. Например, утверждение «треугольник является равнобедренным (p) тогда и только тогда, когда углы при его основании равны (q)» формализуется формулой p ~ q. Эквивалентность можно выразить через импликацию ® и конъюнкцию Ù: p ~ q = (p ® q) Ù (q ® p).

6.2. Приложения алгебры логики в технике.

В технике автоматического управления широко используются релейно-контактные (переключательные) схемы (РКС). Под такой схемой понимают схематическое изображение некоторого устройства, состоящее из переключателей, соединяющих их проводников, входов в схему и выходов из нее. Переключатели - это различные механические устройства, электромагнитные реле, полупроводники и т.д. Они могут находиться только в двух состояниях «замкнутом» и «разомкнутом». Входы и выходы схемы называют ее полюсами, в их качестве могут выступать клеммы, на которые подается напряжение.

Простейшая схема содержит один переключатель Р и имеет один вход А и один выход В.

А В

Переключателю Р ставится в соответствие высказывание р - «переключатель Р замкнут». Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В, т.е. схема пропускает сигнал. Если р ложно, то переключатель разомкнут, и схема не проводит сигнал. Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы. Конъюнкции двух высказываний p Ù q ставится в соответствие схема:

AB

A B

Т.к. любая формула алгебры логики может быть записана в ДНФ, то каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики.

Пример 6.1. Составить РКС для формулы: .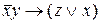

Сначала упростим данную формулу с помощью равносильных преобразований: .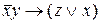

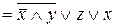
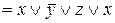
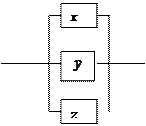РКС для данной формулы имеет вид:

Пример 6.2. Упростить РКС:

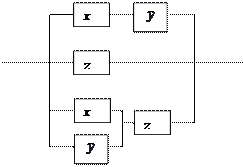Составим для данной РКС формулу (функцию) проводимости и упростим её:

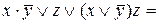
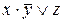, применили закон поглощения к последним двум слагаемым. Упрощенная схема выглядит так:

6.3. УМОЗАКЛЮЧЕНИЯ И ЛОГИЧЕСКИЕ СЛЕДСТВИЯ.

Умозаключения состоят из совокупности утверждений, называемых гипотезами или посылками, и утверждения, называемого следствием. Правильным называется такое умозаключение, следствие которого истинно всякий раз, когда истинны его посылки. Для анализа рассуждений используют понятие логического следствия.

Определение 6.1. Пусть j - логическая формула и 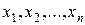- все входящие в нее переменные. Интерпретацией формулы j называется приписывание истинностных значений переменным 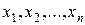, при котором каждому из 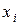, 1£ i £ п, приписано значение 0 или 1.

Определение 6.2. Пусть даны формулы 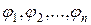и формула j. Говорят, что j есть логическое следствие формул 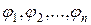, если для всякой интерпретации, в которой формула 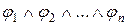истинна, j также истинна. Тогда пишут: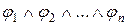 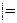j.

Пример 6.3. Я заплатил бы за работу по ремонту телевизора (З), только если бы он стал работать (Р). Он же не работает. Поэтому я платить не буду.

Рассуждение записывается следующим образом: З® Р, Ø Р, следовательно Ø З. Это рассуждение верно, если З® Р Ù Ø Р 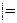Ø З. Построим таблицу истинности:

Из таблицы истинности следует, что Ø З истинно в том случае, когда

З® Р Ù Ø Р истинно. Следовательно, рассуждение верно.

6.4. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ АЛГЕБРЫ

ЛОГИКИ.

Условие логической задачи с помощью соответствующих обозначений записывают в виде формулы алгебры логики. После равносильных преобразований формулы получают ответ на вопросы задачи.

Пример 6.4. По подозрению в совершенном преступлении задержали Брауна, Джона и Смита. Один из них был уважаемым в городе стариком, другой был малоизвестным чиновником, третий - известным мошенником. В процессе следствия старик говорил правду, мошенник лгал, а третий задержанный в одном случае говорил правду, а в другом - ложь. Вот, что они утверждали:

Браун: «Я совершил это. Джон не виноват».

Джон: «Браун не виноват. Преступление совершил Смит».

Смит: «Я не виноват, виновен Браун».

Определите имя старика, мошенника, чиновника и кто из них виноват, если известно, что преступник один.

Решение. Обозначим буквами Б, Д, С высказывания: виноват Браун, виноват Джон, виноват Смит соответственно. Утверждения задержанных можно записать в виде конъюнкций: Б Ù Ø Д, Ø Б Ù С, Б Ù Ø С, из которых по условию задачи, две ложны, а одна истинна. Поэтому будет истинной формула Ф = (Б Ù Ø Д) Ú (Ø Б Ù С) Ú (Б Ù Ø С). Таблица истинности этой формулы:

Формула Ф истинна в пяти из восьми случаев. Случай 5 следует исключить из рассмотрения, т.к. здесь оказываются истинными две конъюнкции, а это противоречит условию задачи. В случаях 4, 6, 7 оказываются истинными по два высказывания Д и С, Б и С, Б и Д соответственно, что также противоречит условию задачи. Следовательно справедлив случай 2, т.е. преступник - Смит. Он - известный мошенник, оба его высказывания ложны: Б Ù Ø С = 0. При этом высказывания Б и Д ложны. Значит, истинна пара высказываний Джона, а у Брауна первое высказывание ложно, а второе истинно. Отсюда ясно, что Джон - уважаемый в городе старик. А Браун - малоизвестный чиновник.

Пример 6.5. После обсуждения состава участников предполагаемой экспедиции было решено, что должны выполняться два условия:

а) если поедет Арбузов, то должны поехать еще Брюквин или Вишневский:

б) если поедет Арбузов и Вишневский, то поедет и Брюквин.

Требуется:

1) ввести краткие обозначения для сформулированных условий и составить логическую формулу, выражающую принятое решение в символической форме;

2) для полученной формулы найти, возможно, более простую равносильную формулу;

3) пользуясь найденной более простой формулой, дать новую словесную формулировку принятого решения.

Решение. Назначение в экспедицию Арбузова, Брюквина, Вишневского обозначим буквами А, Б, В соответственно. Условие а) можно записать в виде: А® Б Ú В, а условие б) в виде А Ù В ® Б. Т.к. оба условия должны выполняться одновременно, то они должны быть соединены логической связкой Ù. Поэтому принятое решение записывается в виде следующей формулы:

(А® Б Ú В) Ù (А Ù В ® Б). Упростим эту формулу и получим:

(А® Б Ú В) Ù (А Ù В ® Б) = (Ø А Ú Б Ú В) (Ø А ÚØ В Ú Б) =

= (Ø А Ú Б) Ú (В ÙØ В) = А® Б.

Последняя формула означает: «если поедет Арбузов, то поедет и Брюквин».